matlab怎么求一个三元一次方程组的解,关于一个三元一次方程的问题（matlab和excel）...

今天碰到一个同学问我一个关于考勤的问题。

每个月他需要工作27天，需要在一天工作4个小时、10个小时、8个小时之前做选择天数，然后凑够一个月180个小时的工时。

数学上看，这就是个“三元一次方程组”问题。如图所示：

很显然，这两个方程构成的面在三维空间中相交，形成一条直线。

(可以matlab实现视觉效果，如图)

代码如下：

[x1,x2]=meshgrid(1:0.1:31);

x3=(180-4x1-10x2)/8;

mesh(x1,x2,x3)

hold on

x3=(27-x1-x2);

mesh(x1,x2,x3);

%plot3 和mesh函数都能画三维的，但是画出来的效果有所不同

但是，我们现在的问题是：如何求出满足这两个方程的整数解呢？

这里我使用了一种方式，用meshgrid函数画网格，并通过find函数找到相关的解。

最后输出的结果：

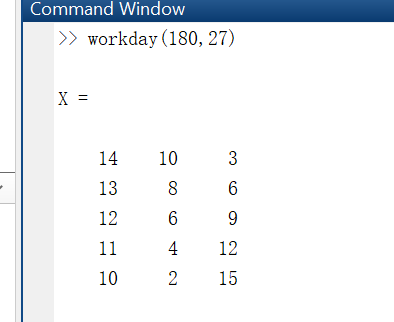
代码如下：

%找出满足约束的工作日分配的整数解

function workday(m,n)

x1=1:31;

x2=1:31;

x3=1:31;

[x1,x2,x3]=meshgrid(x1,x2,x3);

z1=4* x1+10* x2+8* x3;

z2=x1+x2+x3;

k=find(z1== m&z2==n);

X=[x1(k) x2(k) x3(k)]

函数中的m和n分别对应一个月的工时和工作天数，可以根据需要调整。但是这个函数有个问题，就是如果最后求不出整数解，那么输出是empty。事实上，很多情况下一些小数解，是可以被实际接收的。

——————————————————————

用matlab解决了这个问题之后，遇到的一个问题是，很多人并没有装matlab。那么有没有一种更加简单的工具来实现这个问题呢？

我想到了excel。excel是可以求解方程组的。但是经尝试之后，我发现excel只能用来解有确定解的方程组，但是无法求出这种约束问题。

下面给出任何用excel求解方程组。

我们用下面的三个三元一次方程组作为案例。

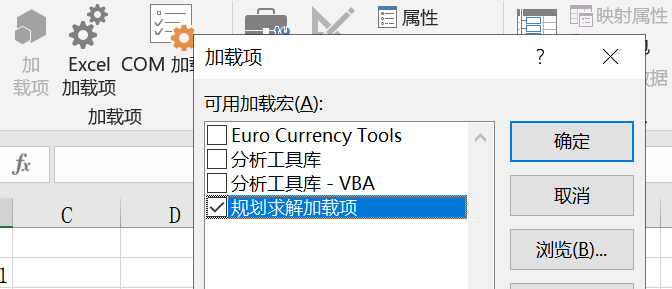
这里需要用到excel上的“规划求解”功能。在任务栏“数据”中。

很多人可能一开始找不到，这是因为这个功能是自选模块，需要在excel“文件”→“选项”→“自定义功能区”→“开发者工具”，勾选上“开发者工具”之后，在excel任务栏中点开“开发者工具”，然后选择“excel加载项”，找到“规划求解”勾选即可。

之后我们建立如图所示的表格，

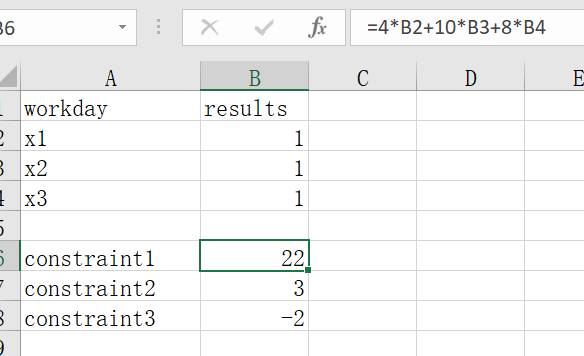
注意，在constraint对应的单元格中输入约束方程。

之后我们点击“规划求解”，然后添加对应的约束和可变单元格，目标单元格。这里注意，目标单元格，应该是三个约束方程中的一个。如下图所示

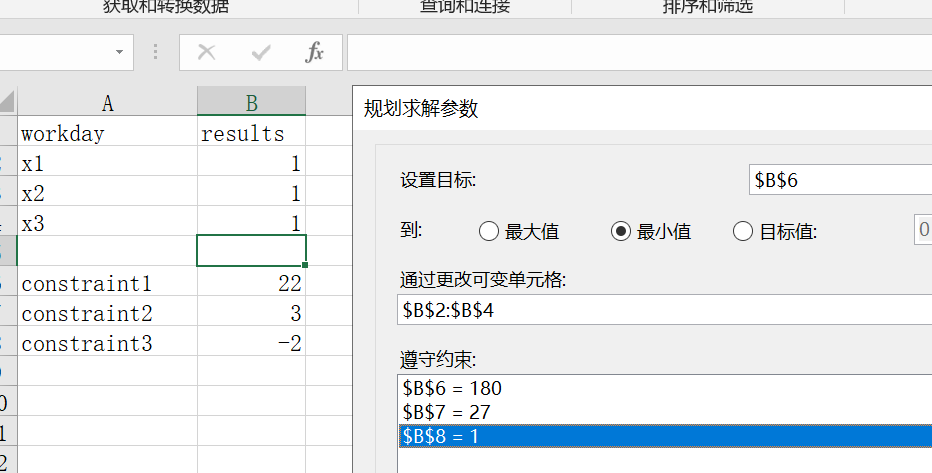
之后，我们选择一种求解方法，点击，即可得到最后结果。

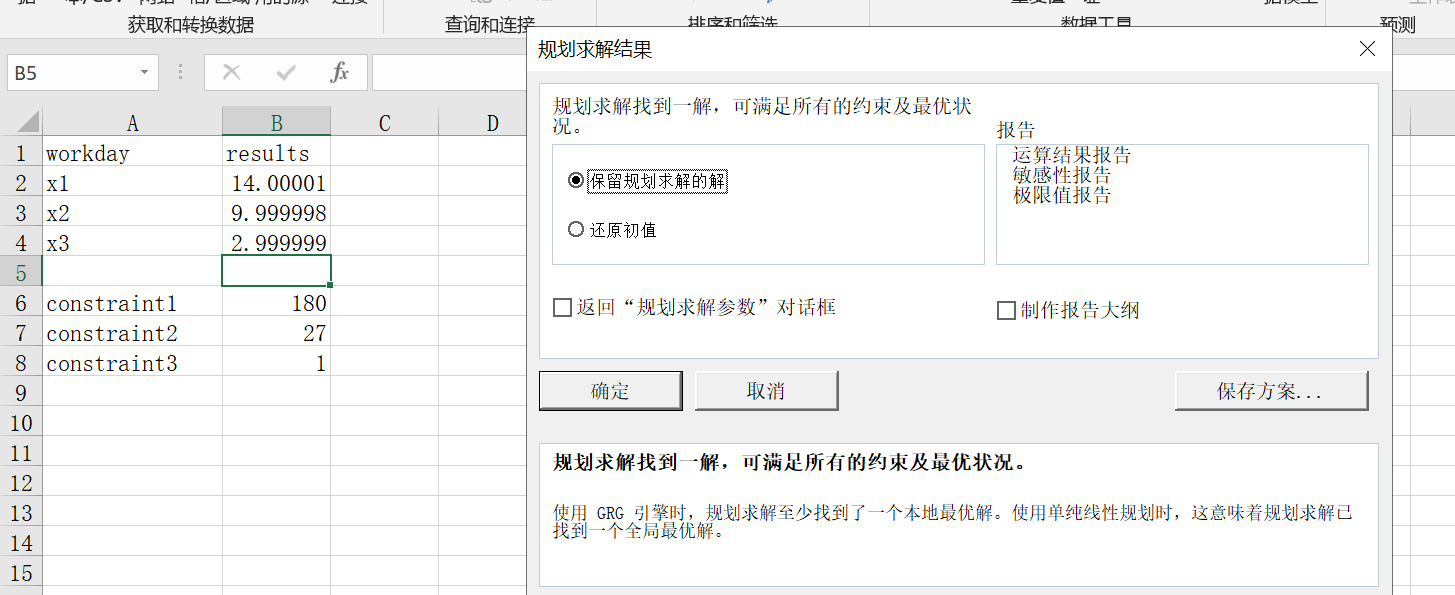
总结：

折腾了半天excel，发现还是matlab好。

标签：一次方程,求解,excel,matlab,x2,x3,x1

来源： https://blog.youkuaiyun.com/JackSword1994/article/details/111045649