1 一阶RC滤波器
电容容抗 ,频率越高,容抗越小
电感感抗 ,频率越高,感抗越大
电阻的阻抗与频率无关,即不同频率下阻碍效果一样。
图1是RC低通滤波电路,电阻和电容组成分压电路,输出电压为


从输出电压公式可知,Xc越大,即频率越低,输出电压越接近输入电压,极限情况频率为0,即直流,输出等于输入,此时电容断路;当频率变高时,Xc减小,输出电压减小,极限情况频率趋于无穷大,输出为0。电容对低频有高容抗,阻碍其通过;高频有低容抗,阻碍小,所以这是一个LPF。
更一般的,求该系统的频率响应函数得

幅频函数为

当w(频率f)很小时,|H(f)|近似为1,信号衰减很小;而当w(频率f)很大时,H(f)近似为0,信号会被阻挡,不能够通过。即为LPF特性。
滤波器的带宽即为3dB带宽(或截止频率),RC低通滤波器的截止频率实际上是输入信号幅度降低3dB的频率(选择该值是因为幅度降低3dB对应于功率降低50%)。因此,截止频率也称为-3 dB频率,实际上该名称更准确且信息量更大。术语带宽是指滤波器通带的宽度,在低通滤波器的情况下,带宽等于-3 dB频率。

截止频率

我们来看一个简单的设计实例。电容值比电阻值更具限制性,因此我们将从常见的电容值(例如10 nF)开始,然后我们将使用该公式来确定所需的电阻值。目标是设计一个滤波器,它将保留5 kHz音频波形并抑制500 kHz噪声波形。我们将尝试100 kHz的截止频率,稍后在文章中我们将更仔细地分析此滤波器对两个频率分量的影响。

因此,160Ω电阻与10 nF电容相结合,将为我们提供一个非常接近所需频率响应的滤波器。用Pspice仿真一阶RC滤波器滤波器。



在上面的设计实例中,R≈160Ω 且 C = 10nF。我们假设V IN的幅度是1 V,这样我们就可以简单地从计算中去掉V IN。首先让我们以正弦波频率计算V OUT的幅度:

正弦波的幅度基本不变。这很好,因为我们的目的是在抑制噪音的同时保持正弦波。这个结果并不令人惊讶,因为我们选择的截止频率(100 kHz)远高于正弦波频率(5 kHz)。现在让我们看看滤波器如何成功衰减噪声分量。
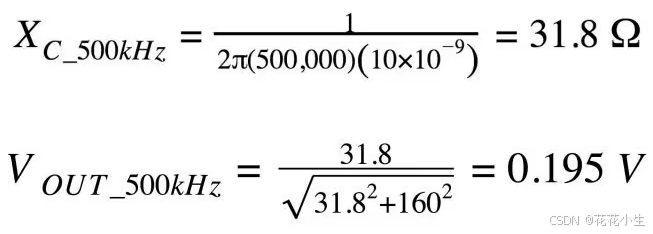
























 1497
1497

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










