NLP（九）：Text-CNN原理及使用Text-CNN文本分类的keras实现

本文链接：https://blog.youkuaiyun.com/weixin_42483560/article/details/89521198

本文深入解析卷积神经网络(CNN)的核心概念，包括卷积运算、反卷积、池化层的工作原理及动机，特别聚焦于Text-CNN在文本分类任务中的应用。通过实例演示了使用Keras实现Text-CNN的过程。

5.利用Text-CNN进行文本分类的keras实现

1. 卷积的定义与动机

1.1 卷积运算的定义

一维卷积的数学形式化定义如下：

$\small S(t) = \int x(t-a)w(a) da$

离散形式如下：

$\small s(t) = \sum\limits_ax(t-a)w(a)$

矩阵形式如下：

$\small s(t)=(X*W)(t)$

其中星号表示卷积。

二维卷积的表达式如下：

$\small s(i,j)=(X*W)(i,j) = \sum\limits_m \sum\limits_n x(i-m,j-n) w(m,n)$

而在深度学习的CNN中，没有‘翻转’这一步，因此表达式是如下形式：

$\small s(i,j)=(X*W)(i,j) = \sum\limits_m \sum\limits_n x(i+m,j+n) w(m,n)$

我们叫W为我们的卷积核，也可以把w称为滤波器。而X则为我们的输入。如果X是一个二维输入的矩阵，而W也是一个二维的矩阵。但是如果X是多维张量，那么W也是一个多维的张量。

1.2 卷积层的计算原理

在下图这个例子中，输入数据是有高长方向的形状的数据，滤波器也一样，有高长方向上的维度。假设用（height, width）表示数据和滤波器的形状，则在本例中，输入大小是(4, 4)，滤波器大小是(3, 3)，输出大小是(2, 2)。

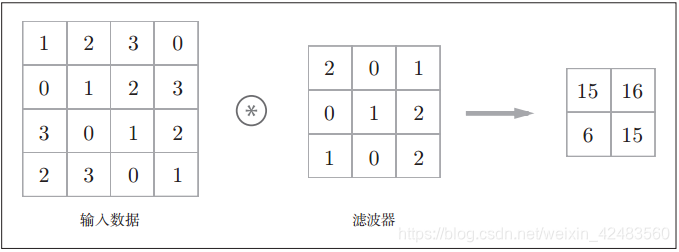
现在用另一张图解释以下运算过程：对于输入数据，卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指下图中灰色的3 × 3的部分。如下图所示，将各个位置上滤波器的元素和输入的对应元素相乘，然后再求和（有时将这个计算称为乘积累加运算）。然后，将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍，就可以得到卷积运算的输出。

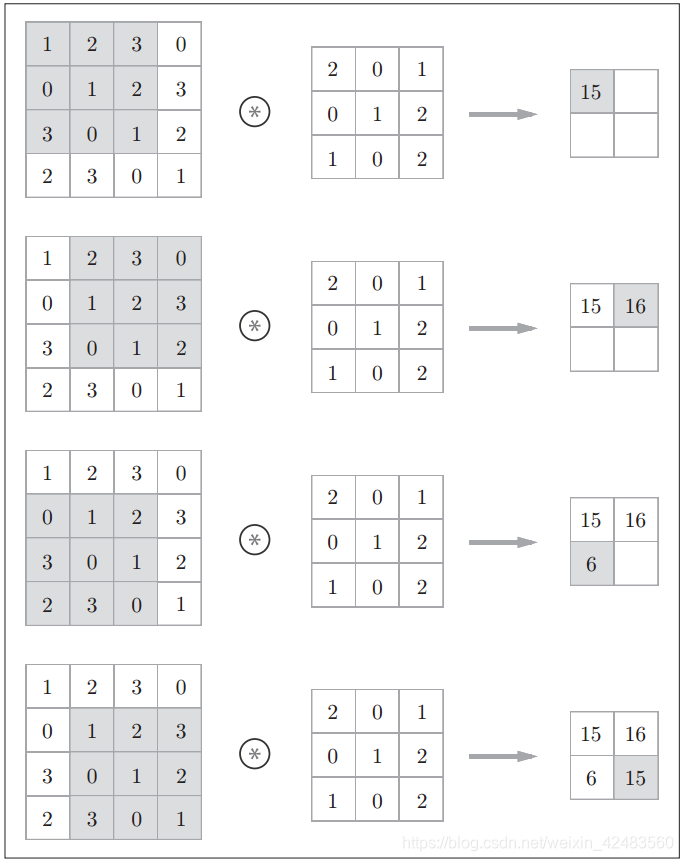
在全连接的神经网络中，除了权重参数，还存在偏置。 CNN中，滤波器的参数就对应之前的权重。并且， CNN中也存在偏置。包含偏置的卷积运算的处理流如下图：

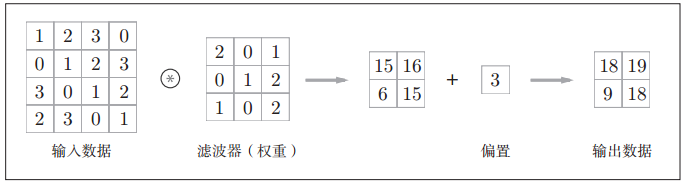
在卷积运算过程中需要制定两个参数：‘“是否填充padding”’和“步幅大小”。

1.3卷积运算的动机

1.3.1 稀疏交互（sparseinteractions）

卷积运算通过三个重要的思想来帮助改进机器学习系统：稀疏交互（sparseinteractions）、参数共享（parameter sharing）、等变表示（equivariant representations）。

传统的神经网络使用矩阵乘法来建立输入与输出的连接关系。其中，参数矩阵中每一个单独的参数都描述了一个输入单元与一个输出单元间的交互。这意味着每一个输出单元与每一个输入单元都产生交互。然而，卷积网络具有 稀疏交互（sparse interactions）（也叫做稀疏连接（sparse connectivity）或者稀疏权重（sparse weights））的特征。这是使核的大小远小于输入的大小来达到的。举个例子，当处理一张图像时，输入的图像可能包含成千上万个像素点，但是我们可以通过只占用几十到上百个像素点的核来检测一些小的有意义的特征，例如图像的边缘。这意味着我们需要存储的参数更少，不仅减少了模型的存储需求，而且提高了它的统计效率。这也意味着为了得到输出我们只需要更少的计算量。这些效率上的提高往往是很显著的。如果有 m 个输入和 n 个输出，那么矩阵乘法需要 m × n 个参数并且相应算法的时间复杂度为 O(m × n)（对于每一个例子）。如果我们限制每一个输出拥有的连接数为 k，那么稀疏的连接方法只需要 k × n 个参数以及 O(k × n) 的运行时间。在很多实际应用中，只需保持 k 比 m 小几个数量级，就能在机器学习的任务中取得好的表现。在深度卷积网络中，处在网络深层的单元可能与绝大部分输入是间接交互的，这允许网络可以通过只描述稀疏交互的基石来高效地描述多个变量的复杂交互。

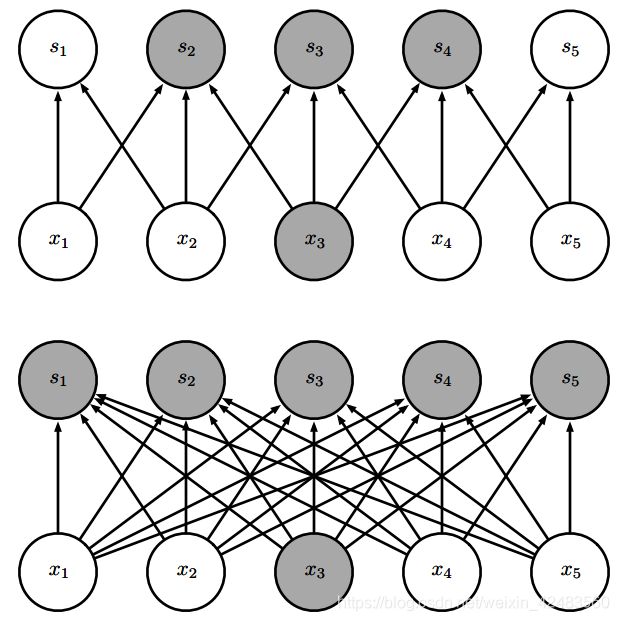
稀疏连接，对每幅图从下往上看。我们强调了一个输入单元 x3 以及在 s 中受该单元影响的输出单元。 (上) 当 s 是由核宽度为 3 的卷积产生时，只有三个输出受到 x 的影响。 (下) 当 s是由矩阵乘法产生时，连接不再是稀疏的，所以所有的输出都会受到 x3 的影响。

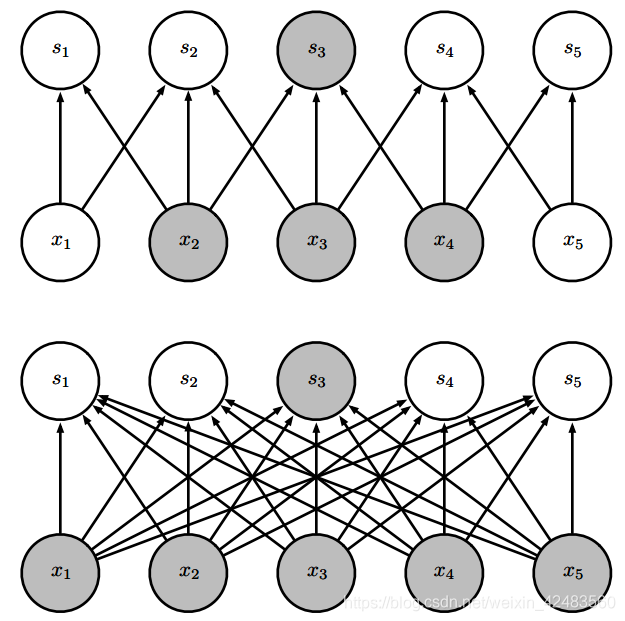
稀疏连接，对每幅图从上往下看。我们强调了一个输出单元 s3 以及 x 中影响该单元的输入单元。这些单元被称为 s3 的接受域（receptive field）。 (上) 当 s 是由核宽度为 3 的卷积产生时，只有三个输入影响 s3。 (下) 当 s 是由矩阵乘法产生时，连接不再是稀疏的，所以所有的输入都会影响 s3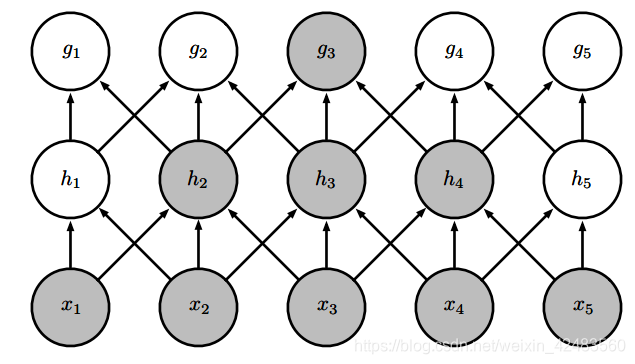

处于卷积网络更深的层中的单元，它们的接受域要比处在浅层的单元的接受域更大。如果网络还包含类似步幅卷积或者池化之类的结构特征，这种效应会加强。这意味着在卷积网络中尽管直接连接都是很稀疏的，但处在更深的层中的单元可以间接地连接到全部或者大部分输入图像。

1.3.2 参数共享（parameter sharing）

参数共享（parameter sharing）是指在一个模型的多个函数中使用相同的参数。在传统的神经网络中，当计算一层的输出时，权重矩阵的每一个元素只使用一次，当它乘以输入的一个元素后就再也不会用到了。作为参数共享的同义词，我们可以说一个网络含有绑定的权重（tied weights），因为用于一个输入的权重也会被绑定在其他的权重上。在卷积神经网络中，核的每一个元素都作用在输入的每一位置上（是否考虑边界像素取决于对边界决策的设计）。卷积运算中的参数共享保证了我们只需要学习一个参数集合，而不是对于每一位置都需要学习一个单独的参数集合。这虽然没有改变前向传播的运行时间（仍然是 O(k × n)），但它显著地把模型的存储需求降低至 k 个参数，并且 k 通常要比 m 小很多个数量级。因为 m 和 n 通常有着大致相同的大小， k 在实际中相对于 m × n 是很小的。因此，卷积在存储需求和统计效率方面极大地优于稠密矩阵的乘法运算。如下图所示：

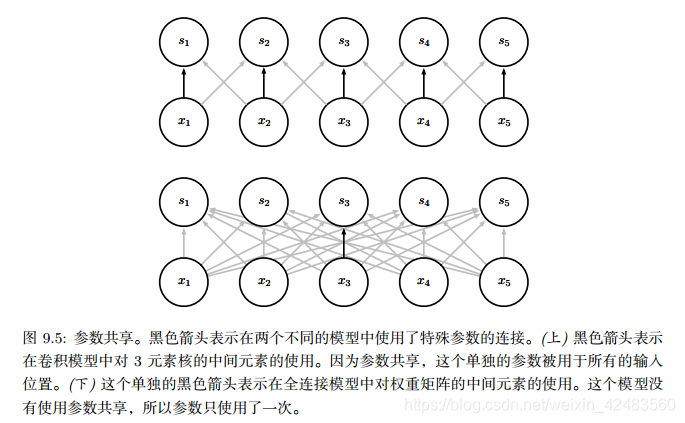
1.3.3 等变表示

对于卷积，参数共享的特殊形式使得神经网络层具有对平移等变（equivariance）的性质。如果一个函数满足输入改变，输出也以同样的方式改变这一性质，我们就说它是等变 (equivariant) 的。

2. 反卷积

反卷积可以简单理解为卷积层运算的逆过程，当做从一个通过卷积运算后缩小的特征图去恢复初始图。

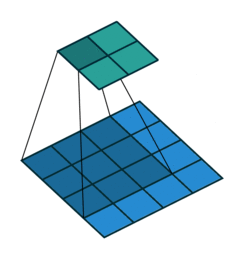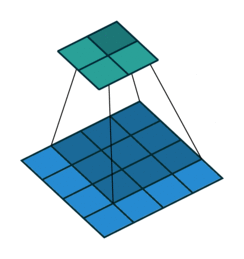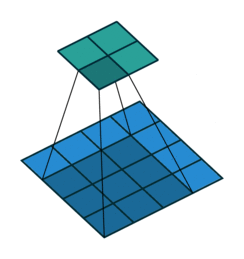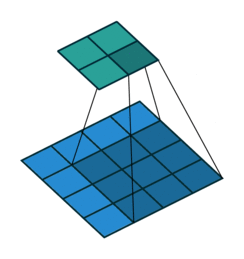
$å·ç§¯ $\ padding=0,stride=1$$

这个图是卷积层求取过程（从蓝色到绿色）

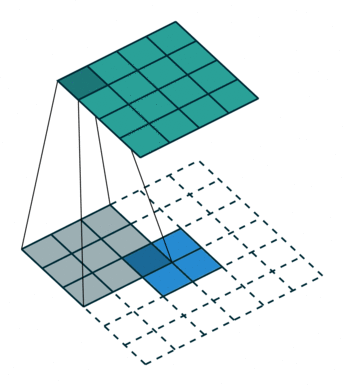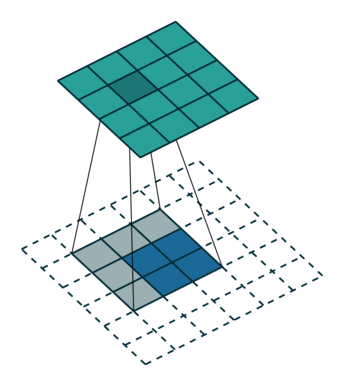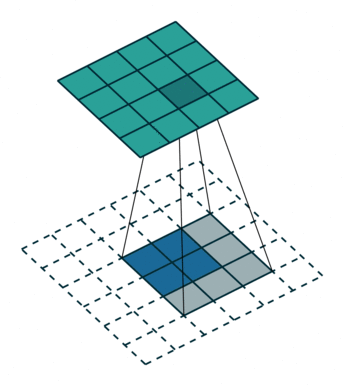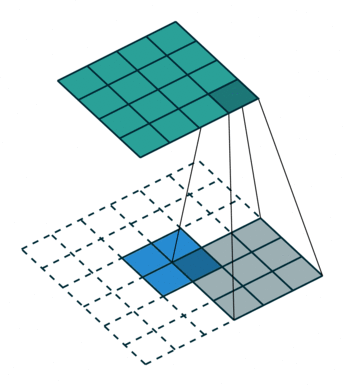
$åå·ç§¯$\ padding=0,stride=1$$

这个图是反卷积层求取过程（从绿色到蓝色）

3. 池化层的定义、种类和动机

3.1 池化运算的定义

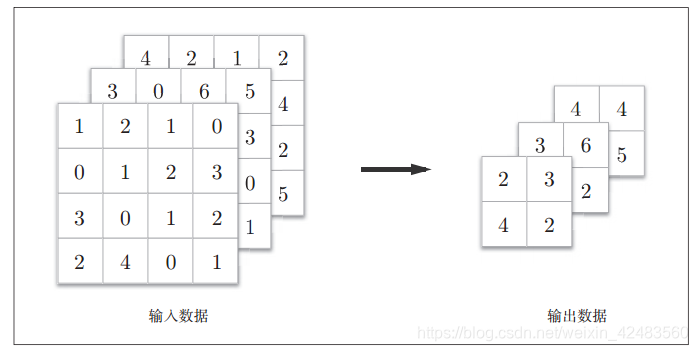
池化是缩小高、长方向上的空间的运算。比如，如下图所示为Max池化的处理顺序，进行将2 × 2的区域集约成1个元素的处理，缩小空间大小。

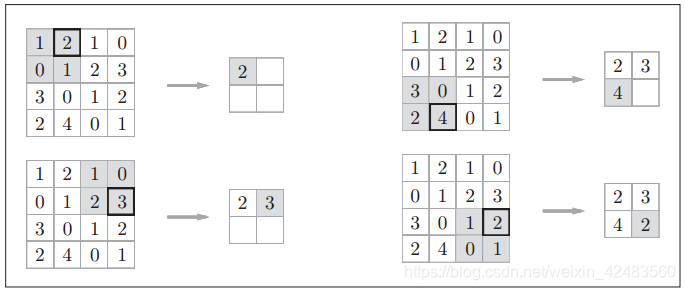
上图的例子是按步幅2进行2 × 2的Max池化时的处理顺序。“Max池化”是获取最大值的运算，“2 × 2”表示目标区域的大小。如图所示，从
2 × 2的区域中取出最大的元素。此外，这个例子中将步幅设为了2，所以2 × 2的窗口的移动间隔为2个元素。另外，一般来说，池化的窗口大小会和步幅设定成相同的值。比如， 3 × 3的窗口的步幅会设为3， 4 × 4的窗口的步幅会设为4。

池化层的特征：

1）没有要学习的参数

池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。

2）通道数不发生变化
经过池化运算，输入数据和输出数据的通道数不会发生变化。如下图所示计算是按通道独立进行的。

3）对微小的位置变化具有鲁棒性（健壮）

输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对输入数据的微小偏差具有鲁棒性。

3.2 池化层的种类

除了Max池化之外，还有Average池化等。相对于Max池化是从目标区域中取出最大值，Average池化则是计算目标区域的平均值。在图像识别领域，主要使用Max池化。

3.3 池化的动机

（1）首要作用，下采样（downsamping）

（2）降维、去除冗余信息、对特征进行压缩、简化网络复杂度、减小计算量、减小内存消耗等等。各种说辞吧，总的理解就是减少参数量。

（3）实现非线性（这个可以想一下，relu函数，是不是有点类似的感觉？）。

（4）可以扩大感知野。

（5）可以实现不变性，其中不变形性包括，平移不变性、旋转不变性和尺度不变性（暂未理解透彻）

4.Text-CNN原理

CNN模型首次使用在文本分类，是Yoon Kim发表的“Convolutional Neural Networks for Sentence Classification”论文中。

NLP的输入是一个个句子或者文档。句子或文档在输入时经过embedding（word2vec或者Glove）会被表示成向量矩阵，其中每一行表示一个词语，行的总数是句子的长度，列的总数就是词表的长度。例如一个包含十个词语的句子，使用了100维的embedding，最后我们就有一个输入为10x100的矩阵。

在CV中，filters是以一个patch（任意长度x任意宽度）的形式滑过遍历整个图像，但是在NLP中，对于文本数据，filter不再横向滑动，仅仅是向下移动，filters会覆盖到所有的词表长度，也就是形状为 [filter_size, vocabulary_size]。更为具体地理解可以看下图，输入为一个7x5的矩阵，filters的高度分别为2,3,4，宽度和输入矩阵一样为5。每个filter对输入矩阵进行卷积操作得到中间特征，然后通过pooling提取最大值，在池化层到全连接层之前可以加上dropout防止过拟合。最终得到一个包含6个值的特征向量。

放上一张TEXT-CNN的图：

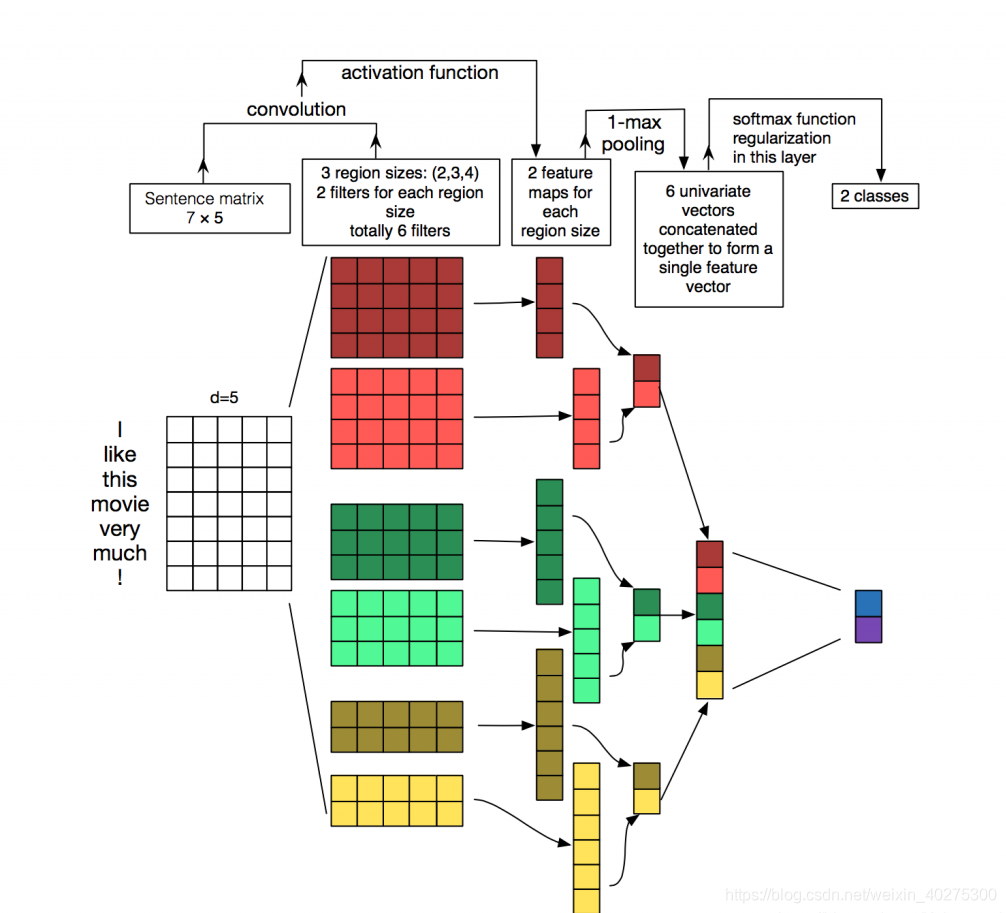
TEXT-CNN

这图中word embedding的维度是5。对于句子 i like this movie very much。可以转换成如上图所示的矩阵AϵR7×5AϵR7×5
有6个卷积核，尺寸为(2×5)(2×5), (3×5)(3×5), 4×54×5，每个尺寸各2个.
样本分别与以上卷积核进行卷积操作，再用激活函数激活。每个卷积核都得到了特征向量(feature maps)
使用1-max pooling提取出每个feature map的最大值，然后在级联得到最终的特征表达。
将特征输入至softmax layer进行分类, 在这层可以进行正则化操作( l2-regulariation)

参数与超参数：

sequence_length （Q: 对于CNN, 输入与输出都是固定的，可每个句子长短不一, 怎么处理? A: 需要做定长处理, 比如定为n, 超过的截断, 不足的补0. 注意补充的0对后面的结果没有影响，因为后面的max-pooling只会输出最大值，补零的项会被过滤掉）
num_classes （多分类, 分为几类）
vocabulary_size （语料库的词典大小, 记为|D|）
embedding_size （将词向量的维度, 由原始的 |D| 降维到 embedding_size）
filter_size_arr （多个不同size的filter）

2015年“A Sensitivity Analysis of (and Practitioners' Guide to) Convolutional Neural Networks for Sentence Classification”论文详细地阐述了关于TextCNN模型的调参心得
---------------------

使用预训练的word2vec 、 GloVe初始化效果会更好。一般不直接使用One-hot。
卷积核的大小影响较大，一般取1~10，对于句子较长的文本，则应选择大一些。
卷积核的数量也有较大的影响，一般取100~600 ，同时一般使用Dropout（0~0.5）。
激活函数一般选用ReLU 和 tanh。
池化使用1-max pooling。
随着feature map数量增加，性能减少时，试着尝试大于0.5的Dropout。
评估模型性能时，记得使用交叉验证。

5.利用Text-CNN进行文本分类的keras实现

"""
-------------------------------------------------
   File Name：     text-cnn
   Description :
   Author :       chaorenfei
   date：          2019/4/25
-------------------------------------------------
   Change Activity:
                   2019/4/25:
-------------------------------------------------
"""
"""
CNN模型首次使用在文本分类，是Yoon Kim发表的“Convolutional Neural Networks for Sentence Classification”论文中。
"""
import tensorflow as tf
from tensorflow import keras
import numpy as np
# from tensorflow.keras.layers import Input, Dense


imdb = keras.datasets.imdb

(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)
############################
# explore data
print("Training entries: {}, labels: {}".format(len(train_data), len(train_labels)))
# >> Training entries: 25000, labels: 25000
print(train_data[0])
# >>
print(len(train_data[0]), len(train_data[1]))
############################
# 将整数转换回字词:了解如何将整数转换回文本可能很有用。在以下代码中，我们将创建一个辅助函数来查询包含整数到字符串映射的字典对象：
# A dictionary mapping words to an integer index
word_index = imdb.get_word_index()

# The first indices are reserved
word_index = {k: (v + 3) for k, v in word_index.items()}
word_index["<PAD>"] = 0
word_index["<START>"] = 1
word_index["<UNK>"] = 2  # unknown
word_index["<UNUSED>"] = 3

reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])


def decode_review(text):
    return ' '.join([reverse_word_index.get(i, '?') for i in text])


# 现在，我们可以使用 decode_review 函数显示第一条影评的文本：
print(decode_review(train_data[0]))
####################################
# prepare data
# 我们可以填充数组，使它们都具有相同的长度，然后创建一个形状为 max_length * num_reviews 的整数张量。我们可以使用一个能够处理这种形状的嵌入层作为网络中的第一层。
# 使用 pad_sequences 函数将长度标准化
train_data = keras.preprocessing.sequence.pad_sequences(train_data,
                                                        value=word_index["<PAD>"],
                                                        padding='post',
                                                        maxlen=256)

test_data = keras.preprocessing.sequence.pad_sequences(test_data,
                                                       value=word_index["<PAD>"],
                                                       padding='post',
                                                       maxlen=256)
# now, the len of data is 256
print(train_data[0])
##########################################
#### stucture the model

convs = []
inputs = keras.layers.Input(shape=(256,))
embed1 = keras.layers.Embedding(10000, 32)(inputs)
# embed = keras.layers.Reshape(-1,256, 32, 1)(embed1)
print(embed1[0])
def reshapes(embed1):
    embed = tf.reshape(embed1, [-1, 256, 32, 1]);
    return embed
# embed = tf.reshape(embed1, [-1, 256, 32, 1])
embed = keras.layers.Lambda(reshapes)(embed1);
print(embed[0])
l_conv1 = keras.layers.Conv2D(filters=3, kernel_size=(2, 32), activation='relu')(embed)  #现长度 = 1+（原长度-卷积核大小+2*填充层大小） /步长 卷积核的形状（fsz，embedding_size）
l_pool1 = keras.layers.MaxPooling2D(pool_size=(255, 1))(l_conv1)  # 这里面最大的不同 池化层核的大小与卷积完的数据长度一样
l_pool11 = keras.layers.Flatten()(l_pool1)    #一般为卷积网络最近全连接的前一层，用于将数据压缩成一维
convs.append(l_pool11)
l_conv2 = keras.layers.Conv2D(filters=3, kernel_size=(3, 32), activation='relu')(embed)
l_pool2 = keras.layers.MaxPooling2D(pool_size=(254, 1))(l_conv2)
l_pool22 = keras.layers.Flatten()(l_pool2)
convs.append(l_pool22)
l_conv3 = keras.layers.Conv2D(filters=3, kernel_size=(4, 32), activation='relu')(embed)
l_pool3 = keras.layers.MaxPooling2D(pool_size=(253, 1))(l_conv3)
l_pool33 = keras.layers.Flatten()(l_pool2)
convs.append(l_pool33)
merge = keras.layers.concatenate(convs, axis=1)

out = keras.layers.Dropout(0.5)(merge)

output = keras.layers.Dense(32, activation='relu')(out)

pred = keras.layers.Dense(units=1, activation='sigmoid')(output)

model = keras.models.Model(inputs=inputs, outputs=pred)
# adam = optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0)
model.summary()
model.compile(loss="binary_crossentropy", optimizer="adam", metrics=['accuracy'])

###############################################################

# validation data
x_val = train_data[:10000]
partial_x_train = train_data[10000:]

y_val = train_labels[:10000]
partial_y_train = train_labels[10000:]
# fit
history = model.fit(partial_x_train, partial_y_train, batch_size=512,
                    epochs=40,
                    validation_data=(x_val, y_val),
                    verbose=1)
# evalute model
results = model.evaluate(test_data, test_labels)

print(results)
# predict data
predictions = model.predict(test_data)
##################################################################
# 创建准确率和损失随时间变化的图
# model.fit() 返回一个 History 对象，该对象包含一个字典，其中包括训练期间发生的所有情况：
history_dict = history.history
print(history_dict.keys())
# >>dict_keys(['loss', 'val_loss', 'val_acc', 'acc'])

# 可以使用这些指标绘制训练损失与验证损失图表以进行对比，并绘制训练准确率与验证准确率图表：
import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(1, len(acc) + 1)
##########-------------画图方式1-----------------

# # "bo" is for "blue dot"
# plt.plot(epochs, loss, 'bo', label='Training loss')
# # b is for "solid blue line"
# plt.plot(epochs, val_loss, 'b', label='Validation loss')
# plt.title('Training and validation loss')
# plt.xlabel('Epochs')
# plt.ylabel('Loss')
# plt.legend()
#
# plt.show()
# # -----------------------------------------
# plt.clf()  # clear figure
# acc_values = history_dict['acc']
# val_acc_values = history_dict['val_acc']
#
# plt.plot(epochs, acc, 'bo', label='Training acc')
# plt.plot(epochs, val_acc, 'b', label='Validation acc')
# plt.title('Training and validation accuracy')
# plt.xlabel('Epochs')
# plt.ylabel('Accuracy')
# plt.legend()

# plt.show()

#######--------画图方式2-------------------
# fig = plt.figure()
# ax = plt.subplot(1,2,1)
# plt.plot(epochs, loss, 'bo', label='Training loss')
# plt.plot(epochs, val_loss, 'b', label='Validation loss')
# plt.title('Training and validation loss')
# plt.xlabel('Epochs')
# plt.ylabel('Loss')
# plt.legend()
#
# ax2 = plt.subplot(1,2,2)
# acc_values = history_dict['acc']
# val_acc_values = history_dict['val_acc']
#
# plt.plot(epochs, acc, 'bo', label='Training acc')
# plt.plot(epochs, val_acc, 'b', label='Validation acc')
# plt.title('Training and validation accuracy')
# plt.xlabel('Epochs')
# plt.ylabel('Accuracy')
# plt.legend()
#
# plt.show()