MATLAB实现的PCM仿真与编码技术全解

最新推荐文章于 2025-05-03 12:22:06 发布

SunLife灬丿七苦

最新推荐文章于 2025-05-03 12:22:06 发布

阅读量1.1k

点赞数 23

本文链接：https://blog.youkuaiyun.com/weixin_42465332/article/details/143102381

版权

本文还有配套的精品资源，点击获取

简介：脉冲编码调制（PCM）是模拟信号数字化的关键技术，广泛应用于多种数据处理。本文档提供了PCM仿真程序的压缩包，详细讲解了PCM的工作原理及其在MATLAB中的实现方法。介绍了采样、量化和编码三个核心步骤，并通过实际操作演示如何使用MATLAB函数对音频信号进行PCM处理，以及如何通过调整采样率和量化位数来优化信号质量。该仿真程序是理解数字信号处理和深入研究PCM性能的实用工具。 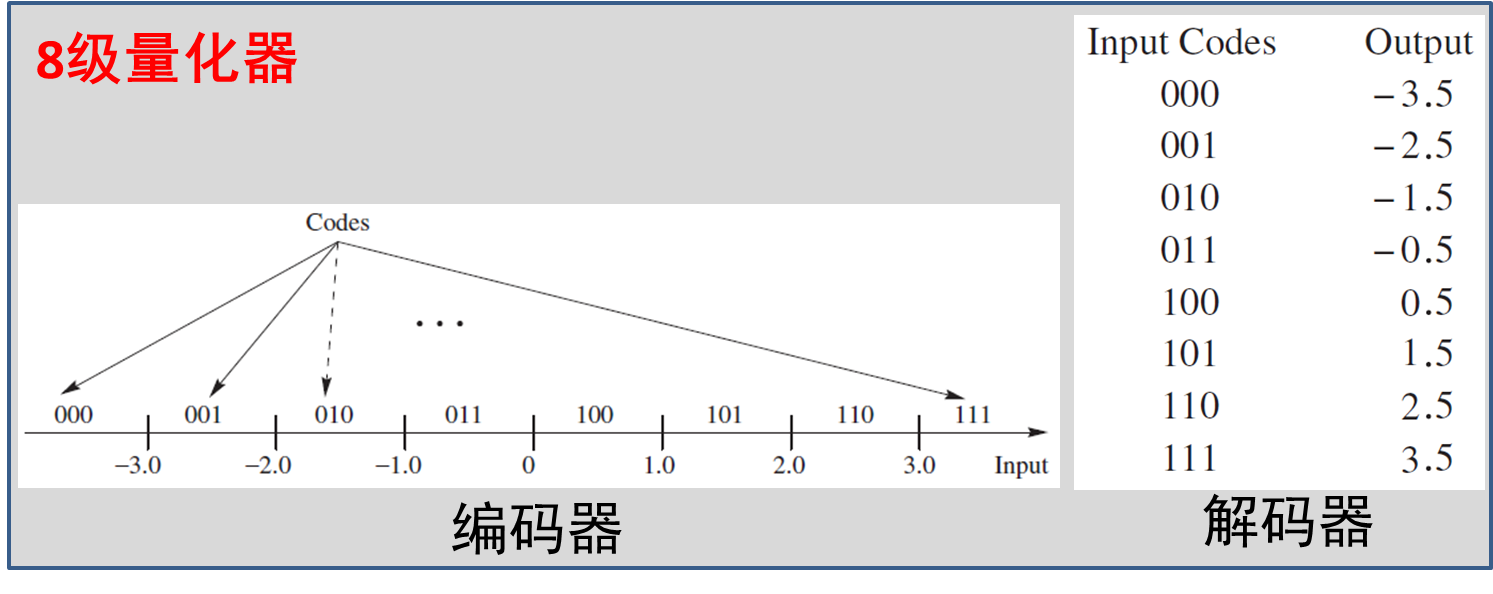PCM编码

1. PCM技术概述

脉冲编码调制（PCM）是一种广泛应用于数字通信领域的技术，它将模拟信号转换成数字形式。这一章节将为读者提供PCM技术的初步介绍，并概述其在通信和数据存储领域的重要性。

PCM技术的发展背景

PCM技术的起源可追溯至20世纪初，随着电子学与数字计算技术的发展，它逐渐成为音频和视频信号处理的支柱。其核心技术在于，通过三个步骤：采样、量化和编码，将连续的模拟信号转换为数字信号，这使得信号可以更方便地进行存储、传输和处理。

PCM技术的应用场景

PCM技术的应用非常广泛，从最初的固定电话通信，到现在的无线通信、数字广播、以及数字电视等领域。它不仅在音频信号处理方面有着重要的作用，在其他需要高度精确度的测量和控制系统中也扮演着关键角色。随着数字媒体技术的发展，PCM技术也成为了云计算和大数据分析中不可或缺的一环。

通过本章内容，我们能够了解PCM技术的基础概念和应用背景，为后续深入探讨PCM的原理和技术细节奠定基础。

2. PCM核心原理与理论基础

2.1 信号的数字化

2.1.1 模拟信号与数字信号的转换

在信息技术领域，模拟信号和数字信号之间转换是现代通信技术的基础。模拟信号是以连续的方式变化的信号，其变化可以是电流、电压、光强等物理量的变化，而这种变化是连续的，可以取任意值。

数字信号则是由一系列离散的数字值来表示，这些值通常是二进制形式。它们使用数字形式来模拟模拟信号，这就需要一个过程叫做“采样”，即每隔一定的时间间隔取一个信号的样本值。同时还需要一个过程叫做“量化”，即将连续的样本值转换成有限个离散值的过程。最后是编码过程，将这些量化后的离散值进行数字化编码。

数字化过程使信息处理更方便，而且数字信号在传输过程中更不容易受到噪声的影响。数字信号的存储、复制等操作几乎不会引入额外的误差，这是模拟信号无法比拟的。

2.1.2 信号数字化的意义与应用

信号数字化的应用是全方位的，它不仅广泛应用于通信领域，如手机、互联网、卫星通信等，还广泛应用于音频和视频处理、医疗成像、数据存储和处理等领域。

数字化允许使用计算机处理和传输信号，这在音频、视频存储和传播方面带来了革命性的变化。例如，音乐和电影在数字化之前需要物理介质进行存储和分发，如唱片和胶片。数字化后，这些内容可以以数字文件的形式存储和传输，大大提高了效率和质量。

数字化的另一个重要应用是在数据压缩和错误校验方面。数字化信号更容易进行压缩，以节省存储空间和传输带宽。同时，数字信号还容易进行错误检测和校正，确保信息的完整性和可靠性。

2.2 脉冲编码调制的基础

2.2.1 脉冲编码调制（PCM）的定义

脉冲编码调制（PCM）是一种用于对模拟信号进行数字编码的技术。它通常用于电话系统、数字电视广播、数字音频录制等。在PCM中，模拟信号被周期性地采样，然后将每个样本的幅度量化成一个数字值，接着用一串二进制数字来表示这些量化值。这个过程包括三个基本步骤：采样、量化、编码。

采样是指按照一定的时间间隔对模拟信号的幅度进行测量，量化则涉及到将这些测量值映射到一组离散的数值上。最后，编码过程将这些量化后的数值转换成二进制数。

2.2.2 PCM系统的组成与工作流程

PCM系统通常由以下几部分组成：

模拟信号源 ：这是需要被数字化的原始模拟信号源。
采样器 ：负责按照奈奎斯特定理规定的频率对信号进行采样。
量化器 ：将采样得到的样本值映射到有限数量的离散幅值上。
编码器 ：将量化后的离散幅值转换成二进制代码。
传输介质 ：数字信号需要通过某种介质传输到接收端。
解码器/还原器 ：将接收到的二进制代码还原成模拟信号。
低通滤波器 ：还原信号后，通过低通滤波器去除因采样和量化引入的高频噪声。

PCM系统的工作流程大体如下：

采样：信号源输出的模拟信号被采样器周期性采样。
量化：每个采样值由量化器量化成最接近的量化级。
编码：量化后的值被编码器转换为二进制数字。
传输：二进制数字通过传输介质传输至接收端。
解码：在接收端，解码器将二进制数字还原为模拟信号。
还原：还原后的模拟信号通过低通滤波器输出，滤除因采样和量化引入的噪声。

接下来，我们将详细探讨PCM中的采样与量化过程，这是PCM技术中的两个关键步骤。

3. 采样与量化：PCM的关键步骤

3.1 采样原理与奈奎斯特定理

3.1.1 采样的基本概念与原理

在数字信号处理领域，采样是一个将连续时间信号转换为离散时间信号的过程。这个过程对于后续的信号处理至关重要，因为数字计算机只能处理离散的数据。采样原理基于信号的频谱特性，其中连续时间信号通过一个理想低通滤波器，以去除高于采样频率一半的所有频率分量，这个过程称为奈奎斯特采样，采样后的信号可以通过插值恢复原信号。

采样过程通常遵循奈奎斯特定理（Nyquist Theorem），该定理指出，为避免信号混叠现象，采样频率应至少是信号最高频率的两倍。如果采样频率低于这个临界值，那么高频信号的频率分量会出现在低频区域，这种现象称为混叠，是信号处理中希望避免的。

3.1.2 奈奎斯特定理及其重要性

奈奎斯特定理对于信号的正确采样至关重要，因为它设定了采样频率的最低界限。在实际应用中，为了保证信号能够被准确重建，通常会选择一个高于临界值的采样频率，即过采样。

奈奎斯特定理的重要性在于，它确保了通过采样得到的离散信号仍然保留了原始模拟信号的所有重要信息。过采样不仅能够降低混叠的风险，还有助于提高信号重建的质量。例如，在数字音频领域，由于人耳能够听到的频率范围一般在20Hz到20kHz之间，因此标准的CD质量音频信号通常采样率为44.1kHz，远高于20kHz的两倍，即40kHz，以确保音频信号的质量。

3.2 量化过程与信噪比（SNR）

3.2.1 量化的原理与类型

量化是将连续信号的幅度值转化为有限数量的离散值的过程。在PCM系统中，量化通常是均匀的，这意味着模拟信号的整个范围被划分为等间隔的量化级别。每个量化级别的幅度值对应一个二进制码字，通过量化过程，连续信号变成了数字信号。

非均匀量化则是在信号的某些区间使用较小的量化间隔，在其他区间使用较大的量化间隔。这种量化方式可以改善信号的动态范围，并增加信号的感知质量。μ律和A律是两种常见的非均匀量化方法，广泛应用于音频和电话信号的数字化中。

3.2.2 信噪比的计算与分析

信噪比（Signal-to-Noise Ratio，SNR）是衡量信号质量的一个重要参数，它表示了信号能量与噪声能量之间的比例。在量化过程中，量化噪声是不可避免的，它是由量化误差产生的。量化噪声的功率可以通过量化台阶的大小和量化级别的数量来估算。

SNR通常以分贝（dB）为单位进行表示，计算公式为：

[ SNR_{dB} = 10 \cdot \log_{10} \left( \frac{P_{signal}}{P_{noise}} \right) ]

其中，( P_{signal} )是信号的功率，( P_{noise} )是量化噪声的功率。提高量化位数能够显著提升SNR，因为每增加一位，量化台阶减小，量化噪声减小，从而提高信号的质量。

量化是一个权衡的过程，增加量化位数可以减少量化噪声，但同时也会增加系统的复杂度和存储需求。在实际应用中，需要根据实际需求选择合适的量化位数。

graph LR
A[模拟信号] -->|采样| B[采样信号]
B -->|量化| C[量化信号]
C -->|编码| D[数字信号]

在本章节中，我们详细探讨了采样与量化的原理，并分析了奈奎斯特定理在采样中的重要性以及如何通过量化来提高信号的信噪比。采样与量化是PCM系统的关键步骤，它们直接影响到数字化信号的最终质量。在下一章节中，我们将讨论PCM编码的不同方式及其优化方法。

4. PCM编码及其优化

4.1 编码方式

在PCM信号处理中，编码方式的选择直接影响了信号的传输效率和质量。我们可以从两个方向来探讨编码方式：线性编码和非线性编码。

4.1.1 线性编码与非线性编码的区别

线性编码，顾名思义，是按照一定比例关系将原始信号转换为数字信号。这种编码方式的优势在于计算简单、易于实现，但缺点是对于信号中的低幅值部分的分辨率不足，对高幅值部分则会浪费大量的位数。换言之，线性编码在信号动态范围的表现上不够优秀。

非线性编码是为了解决线性编码缺点而出现的，常见的非线性编码标准有μ-law编码和A-law编码，尤其在电话通信中使用广泛。非线性编码通过压缩信号的低幅值部分和扩展高幅值部分，提高了信号的动态范围，改善了人耳对声音的感知能力，尤其是在语音通信中。

4.1.2 常见的编码标准与格式

在实际应用中，不同的应用场合对编码标准有着特定的要求。例如，CD音频广泛使用16位线性PCM编码，采样率则为44.1kHz。对于专业音频制作，使用的可能是24位PCM编码，采样率更高，如96kHz或192kHz，以获得更好的音质。

除了PCM编码，还有一些特殊的压缩编码格式，如Dolby Digital和DTS，虽然不是PCM编码，但它们是数字音频传输中重要的编码技术，常用于电影和视频游戏的音轨制作。

4.2 PCM参数调整与信号质量优化

在使用PCM进行信号处理时，正确设置和调整关键参数对保证信号质量至关重要。关键参数包括采样率、量化位数和滤波器设计等。

4.2.1 影响PCM信号质量的关键参数

采样率 ：采样率决定了信号的频率响应范围。根据奈奎斯特定理，采样率至少需要是信号最高频率的两倍才能无失真地还原信号。在实践中，为了避免混叠，通常会使用更高的采样率。

量化位数 ：量化位数决定了信号的动态范围。更多位数意味着更细致的量化级别，从而获得更好的信噪比(SNR)。例如，16位量化可提供96dB的理论动态范围，这对于大多数音频应用而言已足够。

滤波器设计 ：为了防止高频信号对采样过程造成影响，通常会在ADC前端设计抗混叠滤波器，而在DAC后端设计平滑滤波器。

4.2.2 信号质量的测试与优化方法

为了评估PCM信号的质量，常用的方法包括测量信噪比(SNR)、总谐波失真(THD)以及动态范围。对于信号质量的优化，可以从调整上述关键参数着手，同时也需要考虑实际应用场景对信号的要求。

通过软件工具进行信号分析和模拟，例如使用MATLAB进行仿真，可以辅助我们更好地理解信号的行为，优化参数设置。在实际应用中，也可能需要通过硬件设备，如数字音频工作站(DAW)中的插件进行动态范围压缩、均衡等处理，进一步提升信号的质量。

对于优化，一个典型的流程包括：

初始参数配置（如采样率、量化位数等）。
信号采集及初步分析。
应用滤波器处理。
评估信号质量并调整参数。
循环以上过程直至达到最佳信号质量。

这个流程并不是一成不变的，应根据具体情况进行调整。在本节后续内容中，我们将通过MATLAB进行一系列仿真，以更直观地展示这些参数如何影响PCM编码信号的质量。

代码示例和参数分析：

% 假设我们有一个音频文件 'audio.wav'
[y, Fs] = audioread('audio.wav'); % 读取音频文件，Fs是采样率

% 为了优化信号质量，我们可能需要调整采样率
Fs_new = 8000; % 新的采样率
y_resampled = resample(y, Fs_new, Fs); % 重新采样音频信号

% 可视化原始音频信号和采样率调整后的信号
t = (0:length(y)-1)/Fs; % 原始时间向量
t_new = (0:length(y_resampled)-1)/Fs_new; % 调整后的采样时间向量

figure;
subplot(2,1,1);
plot(t, y);
title('Original Audio Signal');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(t_new, y_resampled);
title('Resampled Audio Signal');
xlabel('Time (s)');
ylabel('Amplitude');

在上述MATLAB代码中，我们首先读取了音频文件 'audio.wav'，然后通过 resample 函数调整了信号的采样率，并将结果展示出来。这样，我们就可以直观地看到采样率调整前后的变化，评估调整是否达到了改善信号质量的目的。

参数 Fs_new 和 Fs 分别代表新的采样率和原始采样率，通过调整 Fs_new 的值，我们可以尝试不同的采样率对信号质量的影响。该代码块通过绘图展示了原始信号和调整后的信号，提供了可视化分析的依据。

以上就是一个关于PCM编码及其优化的深入讨论，下面将介绍第五章：MATLAB在PCM仿真中的应用。