机器学习算法基础(实战)
监督学习
将自己这几天所学的做了一个汇总,代码在我的github上,可以参考
目录
- K近邻算法(KNN)
- 线性回归算法(Linear Regression)
- 逻辑回归算法(Logistic Regression)
- 决策树
- 支持向量机(SVM)
一、K近邻算法(KNN)
算法原理
K-近邻算法的核心思想是未标记样本的类别,由距离其最近的k个邻居投票来决定。
假设,我们有一个已经标记的数据集,即已知道了数据集每个样本所属的类别。此时,有一个未标记的数据样本,我们的任务就是预测出这个数据样本所属的类别。k-近邻算法的原理时,计算待标记的数据样本,就由这k个距离最近的样本投票产生。
假设X_test为待标记的数据样本,X_train为已标记的数据集,算法原理的为代码如下
- 遍历X_train中的所有样本,计算每个样本与X_test的距离,并把距离保存在Distance数组中。
- 对Distance数据进行排序,取距离最近的k个点,记为X_knn.
- 在X_knn中统计每个类别的个数,即class0在X_knn中有几个样本,class1在X_knn中几个样本以此类推
- 待标记样本的类别,就是X_knn中所占比最大的那个类别
优点:
- 准确性高
- 有较高的容忍度对噪声与异常值
缺点:
- 计算量大(每次都需遍历所有样本)
- 当类别分界不明显时,精度不高
二、线性回归算法(Linear Regression)
预测函数:

Cost function(成本/代价函数)

梯度下降

实现
- 确定学习率:alpha 太大则函数不能收敛,太小则会遇到局部最优解。
- 确定参数起点:一般选择所有参数为1,但可以根据实际情况灵活选择
- 计算参数的下一组值:根据梯度下降公式进行迭代,分别计算出新的theta值,用新的theta值来进行预测。
- 确认成本函数是否收敛
三、逻辑回归算法(Logistic Regression)
算法介绍
逻辑回归输出值在 [0,1]之间,这是与线性回归算法显著区别。常用它来解决分类问题。
预测函数 

代价函数(cost function)
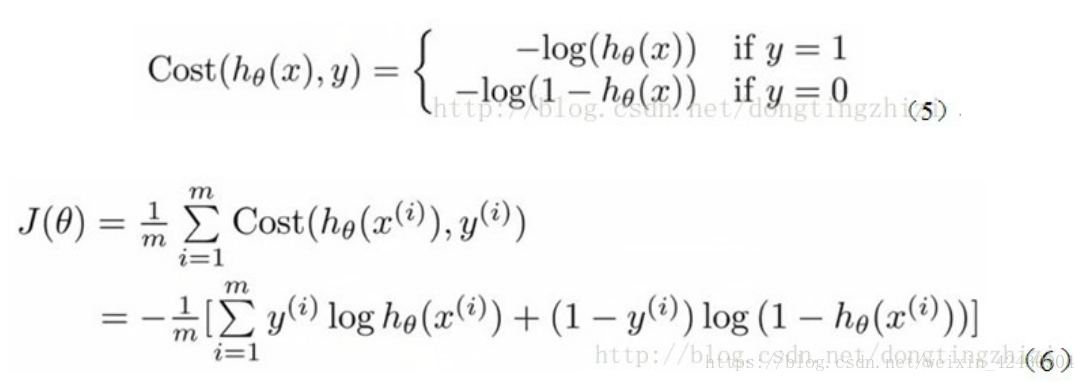
需注意这里需加入正则项来进行惩罚这个代价函数,以免出现过拟合现象。
- 保留所有的特征,减小特征的权重值,确保所有的特征对预测值都有少量的贡献。
- 当每个特征x对预测值y都有少量的贡献时,这样的模型可以很好的进行工作,这就是正则化的目的。
算法参数选择
- 正则化权重即 lambda值的大小
- L1/L2范数的选择
四、决策树
算法介绍
决策树是一个类似与图的树结构,每个分支节点则表示一个特征,根据测试结果进行分类,树叶节点则表示一个类别。
信息熵(Entropy):
H
(
X
)
=
−
∑
x
∈
X
P
(
x
)
l
o
g
2
P
(
x
)
H(X) = -\sum_{x\in X}P(x)log_2P(x)
H(X)=−x∈X∑P(x)log2P(x),信息熵越小,则数据越纯,需要了解的信息就少
信息熵增益: 增益越大则代表需要了解的信息越多,则选择该节点。(ID3算法)
H
(
D
B
a
s
e
)
−
∑
i
=
1
n
H
(
D
s
u
b
i
)
H(D_{Base})-\sum_{i=1}^n H(D_{sub}^i)
H(DBase)−i=1∑nH(Dsubi)
决策树的创建
- 离散化:将连续的数据离散化,如一群人身高在160-190cm,则可以划分为,160-170,170-180,180-190三个区间,这则是将数据离散化。
- 正则项:因为树一直创建下去,则分到最后可能就是该特征就一个样本则信息熵越小,未避免则加入正则项,来使得算法达到某个平衡。
- 基尼不纯度:也是衡量信息不纯度的指标 G i n i ( D ) = ∑ x ∈ X P ( x ) ( 1 − P ( x ) ) = 1 − ∑ x ∈ X P ( x ) 2 Gini(D) = \sum_{x\in X}P(x)(1-P(x)) = 1-\sum_{x\in X}P(x)^2 Gini(D)=x∈X∑P(x)(1−P(x))=1−x∈X∑P(x)2由上式可知,在P(x) = 1时,Gini(D)=0 数据不纯度最低,纯度最高。
算法参数
- criterion:特征选择算法,可选择entropy 和gini,一般来说两种算法准确度上没什么差别,entropy运算效率会偏低,因为有对数的运算
- splitter:创建决策树分支的选项,一种时选择最优的分支原则,另一种时从排名考前的特征中,随机选择一个特征来创建分支,这个方法和正则项的效果类似,可以避免过拟合。
- max_depth:指定决策树的最大深度,调节该参数可避免过拟合
- min_samples_split:该参数指定创建分支的数据集大小,默认为2.如果一个节点的数据样本数小于该值,将不被创建。是一种前剪枝方法。
- min_samples_leaf:创建分支后的节点样本数量必须大于该值,否则不再创建分支。前剪枝方法。
- max_leaf_nodes:限制最大的样本节点数
- min_impurity_split:可以使用该值来指定信息增益的阈值,创建分支时,信息增益必须大于该值才能创建成功。
五、支持向量机(SVM)
算法介绍
如图所示,可以构造一个分割线把圆和正方形给分割开来,这个分割线就是分割超平面(Separating hyperplane).由图可以看出,实线的分割效果比虚线的好,即margin2 >margin1,margin2 的两倍称为间距(margin)。那些离分离超平面最近的电,称为支持向量(support vector)


向量A到分割超平面的距离
d
=
∣
w
T
A
+
b
∣
∣
w
∣
∣
d = \frac{|w^TA+b}{||w||}
d=∣∣w∣∣∣wTA+b
由于A在该线上,则
w
T
A
+
b
=
1
w^TA+b=1
wTA+b=1上,带入上式得,
d
=
1
∣
∣
w
∣
∣
d = \frac{1}{||w||}
d=∣∣w∣∣1 ,
∣
∣
w
∣
∣
||w||
∣∣w∣∣为L2范数,其计算公式为:
∣
∣
w
∣
∣
=
∑
i
=
1
n
w
i
2
||w|| = \sqrt{\sum_{i=1}^nw_i^2}
∣∣w∣∣=i=1∑nwi2
由此可以求
1
∣
∣
w
∣
∣
\frac{1}{||w||}
∣∣w∣∣1的最大值,即求
∣
∣
w
∣
∣
2
||w||^2
∣∣w∣∣2的最小值:
∣
∣
w
∣
∣
2
=
∑
j
=
1
n
w
j
2
||w||^2=\sum_{j=1}^nw_j^2
∣∣w∣∣2=∑j=1nwj2
常用核函数
- 线性核函数: K ( x ( i ) , x ( j ) ) = x ( i ) T x ( j ) K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)} K(x(i),x(j))=x(i)Tx(j)
- 多项式核函数: K ( x ( i ) , x ( j ) ) = ( γ x ( i ) T x ( j ) + c ) n K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}x^{(j)}+c)^n K(x(i),x(j))=(γx(i)Tx(j)+c)n
- 高斯核函数: K ( x ( i ) , x ( j ) ) = e x p ( − x ( i ) − x ( j ) 2 σ 2 ) K(x^{(i)},x^{(j)})=exp(-\frac {x^{(i)}-x^{(j)}}{2\sigma^2}) K(x(i),x(j))=exp(−2σ2x(i)−x(j))
代码参考我的Github
























 1771
1771

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








