图的基本概念:
图是由边集E和点集V构成集合:
G
(
V
,
E
)
G(V,E)
G(V,E)
无向边:
(
v
i
,
v
j
)
(v_i,v_j)
(vi,vj) ,有向边:
<
v
i
,
v
j
>
<v_i,v_j>
<vi,vj>
逻辑关系:点之间的逻辑关系为邻接,邻接的点简称邻点。
简单图:一般只讨论简单图,所谓简单图就是没有自边(自身指向自身)也没有重复边,自边和重复边在计算机和现实中大多是没有意义的。
图的分类:对于图来说,常见的有三种分类方法:
边上是否加权:加权:网图/网,不加权:图
边是否有向:有向图、无向图
任意两点是否可达:连通图、非连通图
对于非连通图,不连通的子图称为连通分量,对于每个连通分量来说,本身必须是一个连通图。如下图:a图中有三个连通分量,每个连通分量就是一个连通图,如图b。

图的数据结构:
一般有两种数据结构:邻接矩阵和邻接表。
邻接矩阵:一般是一个二维数组vector<vector<type>> V, type为节点的数据类型。
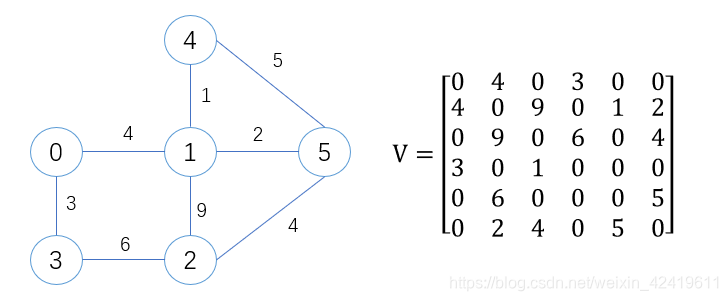
无向图的邻接矩阵:一定是对称矩阵,非网图中,
V
[
i
]
[
j
]
=
0
,
1
V[i][j]=0,1
V[i][j]=0,1表示边
e
i
j
e_{ij}
eij是否存在,网图中,
V
[
i
]
[
j
]
V[i][j]
V[i][j]表示边
e
i
j
e_{ij}
eij的权重,无边则用0或者
∞
∞
∞表示,如下图:

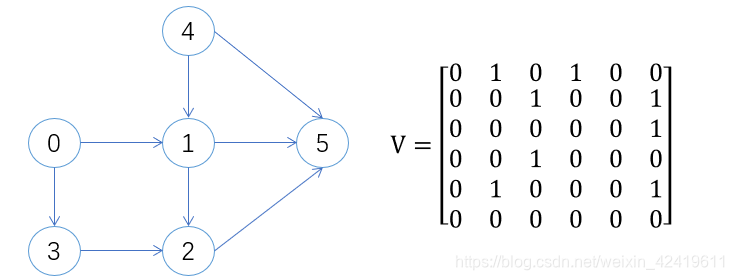
有向图的邻接矩阵:一般不对称

邻接表:每个点都设置一个邻点向量/链表。
即<
v
i
v_{i}
vi,vector<type>>,type为点的数据类型。如果是网图,type改成二元字典map<type,int>, 即<
v
i
v_{i}
vi,vector<map<type,int>>>
一般用向量保存各点的邻点,链表不易随机存取。
如上面两个有向图的邻接表分别为:

我更偏爱用邻接表保存图的信息,一是不容易搞错(点和邻点的一 一对应关系),二是对于稀疏图来说,邻接表更省空间,遍历时也更省时间!







 本文深入探讨了图的基本概念,包括无向边与有向边、简单图、图的分类,以及图的数据结构——邻接矩阵和邻接表。详细解析了不同类型的图和它们在实际应用中的意义。
本文深入探讨了图的基本概念,包括无向边与有向边、简单图、图的分类,以及图的数据结构——邻接矩阵和邻接表。详细解析了不同类型的图和它们在实际应用中的意义。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










