BST，AVL的c++实现

最新推荐文章于 2023-12-17 11:59:45 发布
最新推荐文章于 2023-12-17 11:59:45 发布
阅读量257 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 数据结构 文章标签： 二叉搜索树 BST 平衡二叉树的实现 AVL
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_42405632/article/details/88080343
本文介绍使用C++实现二叉搜索树(BST)和平衡二叉树(AVL)的方法，包括插入、删除、查找等核心操作，并提供详细的代码实现及验证。通过实例演示了如何使用这些数据结构进行数据的高效管理。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1.BST二叉搜索树的c++实现及验证

/************************************************************************
    > File Name: BST.cpp
    > Author: wpf
    > Mail: wpf9264@163.com 
    > Created Time: 2019年03月01日 星期五 16时12分17秒
************************************************************************/

#include<iostream>
using namespace std;

template<typename Comparable>
class BST
{
	private:
		//树节点
		struct BinaryNode
		{
			Comparable	element;
			BinaryNode	*left;
			BinaryNode	*right;

			BinaryNode(const Comparable & x,BinaryNode *lt,BinaryNode *rt):element{x},left{lt},right{rt}
			{}

			BinaryNode(Comparable && x,BinaryNode *lt,BinaryNode *rt):element{std::move(x)},left{lt},right{rt}
			{}
		};

		BinaryNode *root;

	public:
		BST()
		{ 
			root = NULL;
		}

		BST(const Comparable & x)
		{
			root = new BinaryNode{x,NULL,NULL};
		}
		//拷贝构造
		BST(const BST & rhs):root{NULL}
		{
			root = clone(rhs.root);
		}
		//移动构造
		BST(BST && rhs):root{std::move(rhs.root)}
		{ }
		//析构
		~BST()
		{
			makeEmpty();
		}

		BST & operator=(const BST & rhs)
		{
			if(this != &rhs)
			{
				BST tmp{rhs};
				std::swap(*this,tmp);			
			}

			return *this;
		}

		BST & operator=(BST && rhs)
		{
			std::swap(root,rhs.root); 
		}
		const Comparable & findMin()const
		{
			return findMin(root)->element;
		}

		const Comparable & findMax()const
		{
			return findMax(root)->element;
		}

		bool contains(const Comparable & x)const
		{
			return contains(x,root);
		}

		bool isEmpty()const
		{
			return root == NULL;
		}

		void printTree(ostream & out = std::cout)const
		{
			printTree(root,out);
			out<<endl;
		}
		
		void makeEmpty()
		{
			makeEmpty(root);
		}

		void insert(const Comparable & x)
		{
			insert(x,root);
		}

		void insert(Comparable && x)
		{
			insert(x,root);
		}

		void remove(const Comparable & x)
		{
			remove(x,root);
		}

	private:

		//插入函数的左值版本
		void insert(const Comparable & x,BinaryNode* & t)
		{
			if(t == NULL)
				t = new BinaryNode{x,NULL,NULL};
			else if(x < t->element)
				insert(x,t->left);
			else if(x > t->element)
				insert(x,t->right);
			else
				;
		}
		//插入函数的右值版本
		void insert(Comparable && x,BinaryNode* & t)
		{
			if(t == NULL)
				t = new BinaryNode*{std::move(x),NULL,NULL};
			else if(x < t->element)
				insert(std::move(x),t->left);
			else if(x > t->element)
				insert(std::move(x),t->right);
			else
				;
		}
		//删除函数
		void remove(const Comparable & x,BinaryNode * & t)
		{
			if(t == NULL)
				return;

			if(x < t->element)
				remove(x,t->left);
			else if(x > t->element)
				remove(x,t->right);
			else if(t->left !=NULL  &&  t->right != NULL)	//找到了x,并且它有两个孩子
			{
				t->element = findMax(t->right)->element;
				remove(t->element,t->right);
			}
			else	//ｘ只有一个孩子，或者没有孩子
			{
				BinaryNode* oldNode = t;
				t = (t->left != NULL)?t->left:t->right;
				delete oldNode;
			}
		}
		//最小值
		BinaryNode* findMin(BinaryNode* t)const
		{
			if(t != NULL)
				while(t->left != NULL)
					t = t->left;
			return t;
		}
		//最大值
		BinaryNode* findMax(BinaryNode* t)const
		{
			if( t == NULL)
				return NULL;
			if(t->right == NULL)
				return t;
			return findMax(t->right);
		}
		//查询函数
		bool contains(const Comparable & x,BinaryNode* t)const
		{
			if(t == NULL)
				return false;
			else if(x > t->element)
				contains(x,t->right);
			else if(x < t->element)
				contains(x,t->left);
			else
				return true;
		}
		//清空
		void makeEmpty(BinaryNode* & t)
		{
			if(t != NULL)
			{
				makeEmpty(t->left);
				makeEmpty(t->right);
				delete t;
			}
			t= NULL;
		}
		//打印函数
		void printTree(BinaryNode*  t,ostream & out)const
		{
			if(t == NULL)
				return;
			//前序，中序，后序仅仅变动打印的顺序即可，很简单
			printTree(t->left,out);
			printTree(t->right,out);
			cout<<t->element<<" ";
		}
		//复制函数，用于拷贝构造
		BinaryNode* clone(BinaryNode* t)const
		{
			if(t == NULL)
				return NULL;
			else
				return new BinaryNode{t->element,clone(t->left),clone(t->right)};
		}
};

int main(int argc,char** argv)
{
	BST<int> b{8};
	b.insert(2);
	b.insert(0);
	b.insert(6);
	b.insert(9);
	b.insert(7);
	b.insert(4);
	cout<<"************ 以下为测试成员函数功能**************"<<endl;
	cout<<"printTree(): ";
	b.printTree();
	cout<<"remove(7)  : ";
	b.remove(7);
	b.printTree();
	cout<<"isEmpty(): "<<b.isEmpty()<<endl;
	cout<<"findMin(): "<<b.findMin()<<endl;
	cout<<"findMax(): "<<b.findMax()<<endl;
	cout<<"contains(10): "<<b.contains(10)<<endl;
	cout<<"contains(0): "<<b.contains(0)<<endl;
	
	cout<<"************	以下为测试构造函数	***************"<<endl;
	BST<int> n;
	cout<<n.isEmpty()<<endl;
	n = b;
	n.printTree();

	return 0;
}

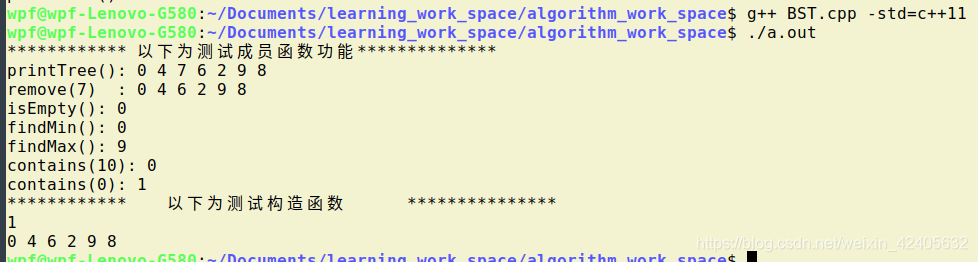
以下为测试结果：
在这里插入图片描述

2.平衡二叉树的c++实现及验证

/************************************************************************
    > File Name: AVL.cpp
    > Author: wpf
    > Mail: wpf9264@163.com 
    > Created Time: 2019年03月02日 星期六 18时11分17秒
************************************************************************/

#include<iostream>
using namespace std;

template<typename Comparable>
class AVL
{
	private:
		//树节点
		struct AvlNode
		{
			Comparable	element;
			AvlNode	*left;
			AvlNode	*right;
			int height;

			AvlNode(const Comparable & x,AvlNode *lt,AvlNode *rt,int h=0):element{x},left{lt},right{rt},height(h)
			{}

			AvlNode(Comparable && x,AvlNode *lt,AvlNode *rt,int h=0):element{std::move(x)},left{lt},right{rt},height{h}
			{}
		};

		AvlNode *root;

	public:
		AVL()
		{ 
			root = NULL;
		}

		AVL(const Comparable & x)
		{
			root = new AvlNode{x,NULL,NULL};
		}
		//拷贝构造
		AVL(const AVL & rhs):root{NULL}
		{
			root = clone(rhs.root);
		}
		//移动构造
		AVL(AVL && rhs):root{std::move(rhs.root)}
		{ }
		//析构
		~AVL()
		{
			makeEmpty();
		}
		//深拷贝
		AVL & operator=(const AVL & rhs)
		{
			if(this != &rhs)
			{
				AVL tmp{rhs};
				std::swap(*this,tmp);			
			}

			return *this;
		}
		//移动复制运算符
		AVL & operator=(AVL && rhs)
		{
			std::swap(root,rhs.root); 
			return *this;
		}
		const Comparable & findMin()const
		{
			return findMin(root)->element;
		}

		const Comparable & findMax()const
		{
			return findMax(root)->element;
		}

		bool contains(const Comparable & x)const
		{
			return contains(x,root);
		}

		bool isEmpty()const
		{
			return root == NULL;
		}

		void printTree(ostream & out = std::cout)const
		{
			if(isEmpty())
				out<<"empty tree";
			else
				printTree(root,out);
			out<<endl;
		}
		
		void makeEmpty()
		{
			makeEmpty(root);
		}

		void insert(const Comparable & x)
		{
			insert(x,root);
		}

		void insert(Comparable && x)
		{
			insert(std::move(x),root);
		}

		void remove(const Comparable & x)
		{
			remove(x,root);
		}

	private:

		//插入函数的右值版本
		void insert(const Comparable & x,AvlNode* & t)
		{
			if(t == NULL)
				t = new AvlNode{x,NULL,NULL};
			else if(x < t->element)
				insert(x,t->left);
			else if(x > t->element)
				insert(x,t->right);
			else
				;
			balance( t );
		}
		//插入函数的左值版本
		void insert(Comparable && x,AvlNode* & t)
		{
			if(t == NULL)
				t = new AvlNode{std::move(x),NULL,NULL,0};
			else if(x < t->element)
				insert(std::move(x),t->left);
			else if(x > t->element)
				insert(std::move(x),t->right);
			else
				;
			balance( t );
		}
		//删除函数
		void remove(const Comparable & x,AvlNode * & t)
		{
			if(t == NULL)
				return;

			if(x < t->element)
				remove(x,t->left);
			else if(x > t->element)
				remove(x,t->right);
			else if(t->left !=NULL  &&  t->right != NULL)	//找到了x,并且它有两个孩子
			{
				t->element = findMax(t->right)->element;
				remove(t->element,t->right);
			}
			else	//ｘ只有一个孩子,或者没有孩子
			{
				AvlNode *oldNode = t;		//记得要释放要删除节点的内存
				t = (t->left != NULL)?t->left:t->right;
				delete oldNode;
			}
			balance( t );
		}
		//最小值
		AvlNode* findMin(AvlNode* t)const
		{
			if(t != NULL)
				while(t->left != NULL)
					t = t->left;
			return t;
		}
		//最大值
		AvlNode* findMax(AvlNode* t)const
		{
			if( t == NULL)
				return NULL;
			if(t->right == NULL)
				return t;
			return findMax(t->right);
		}
		//查询函数,递归版本
		bool contains(const Comparable & x,AvlNode* t)const
		{
			if(t == NULL)
				return false;
			else if(x > t->element)
				contains(x,t->right);
			else if(x < t->element)
				contains(x,t->left);
			else
				return true;
		}
/******非递归版本********************
    bool contains( const Comparable & x, AvlNode *t ) const
    {
        while( t != nullptr )
            if( x < t->element )
                t = t->left;
            else if( t->element < x )
                t = t->right;
            else
                return true;    // Match

        return false;   // No match
    }
*****************************************************/
		//清空
		void makeEmpty(AvlNode* & t)
		{
			if(t != NULL)
			{
				makeEmpty(t->left);
				makeEmpty(t->right);
				delete t;
			}
			t= NULL;
		}
		//打印函数
		void printTree(AvlNode*  t,ostream & out)const
		{
			if(t == NULL)
				return;
			//前序,中序，后序仅仅变动打印的顺序即可，很简单
			printTree(t->left,out);
			printTree(t->right,out);
			cout<<t->element<<" ";
		}
		//复制函数,用于拷贝构造
		AvlNode* clone(AvlNode* t)const
		{
			if(t == NULL)
				return NULL;
			else
				return new AvlNode{t->element,clone(t->left),clone(t->right),t->height};
		}

		int height(AvlNode * t)const
		{
			return t==NULL?-1:t->height;
		}
		int max(int lhs,int rhs)const
		{
			return lhs>rhs?lhs:rhs;
		}

	/**右旋转,对应情形1，以k2为轴，转动k2的左孩子k1     */
    void rotateWithLeftChild( AvlNode * & k2 )
    {
        AvlNode *k1 = k2->left;
        k2->left = k1->right;
        k1->right = k2;
        k2->height = max( height( k2->left ), height( k2->right ) ) + 1;
        k1->height = max( height( k1->left ), k2->height ) + 1;
        k2 = k1;
    }

    /**左旋转,对应情形4，以k2为轴，转动k2的右孩子k1     */
    void rotateWithRightChild( AvlNode * & k2 )
    {
        AvlNode *k1 = k2->right;
        k2->right = k1->left;
        k1->left = k2;
        k2->height = max( height( k2->left ), height( k2->right ) ) + 1;
        k1->height = max( height( k1->right ), k2->height ) + 1;
        k2 = k1;
    }
    /**左-右旋转对应情形2,先旋转k3的左孩子k2的右孩子k1，再旋转k3新的左孩子 */
    void doubleWithLeftChild( AvlNode * & k3 )
    {
        rotateWithRightChild( k3->left );
        rotateWithLeftChild( k3 );
    }

    /*右-左旋转对应情形3,选旋转k3的右孩子k2的左孩子k1，再旋转k3新的右孩子   */
    void doubleWithRightChild( AvlNode * & k1 )
    {
        rotateWithLeftChild( k1->right );
        rotateWithRightChild( k1 );
    }
	    static const int ALLOWED_IMBALANCE = 1;

    // 平衡函数
    void balance( AvlNode * & t )
    {
        if( t == nullptr )
            return;

        if( height( t->left ) - height( t->right ) > ALLOWED_IMBALANCE )
            if( height( t->left->left ) >= height( t->left->right ) )
                rotateWithLeftChild( t );	//情形1
            else
                doubleWithLeftChild( t );	//情形2
        else
        if( height( t->right ) - height( t->left ) > ALLOWED_IMBALANCE )
            if( height( t->right->right ) >= height( t->right->left ) )
                rotateWithRightChild( t );	//情形4
            else
                doubleWithRightChild( t );	//情形3

        t->height = max( height( t->left ), height( t->right ) ) + 1;
    }
};


int main(int argc,char** argv)
{
	AVL<int> b{8};
	b.insert(2);
	b.insert(0);
	b.insert(6);
	b.insert(9);
	b.insert(7);
	b.insert(4);
	cout<<"printTree(): ";
	b.printTree();

	return 0;
}

运行结果显示的是后序排列
在这里插入图片描述

[BST的构建][C++实现]
ChessC的博客
03-29 1145
今天前面碰到一题，判定给定的BST是否是合法的，因为BST性质，LDR遍历递增，根据这个来判定即可。但是碰到给定自行构建BST的时候，给定的输入是这样的： 5 1 5 2 3 1 0 0 3 4 5 4 0 0 6 0 0 什么意思呢，第一行为n和root，分别代表总共n个节点，并且root节点为序号root的节点。 之后每一行输入的是三个数，分别为val，left_idx，...
二分查找树的C++实现 Binary Search Tree（BST）
人生如路
03-13 3435
用C++实现了二叉查找树的 创建 插入 删除 遍历（宽度优先和三种深度优先[前序，中序，后序]） 查找某值 查找最大值和最小值 清空 复制二叉树（深复制） #include #include using namespace std; struct BSTNode { int val; BSTNode *left; BSTNode *right; }; /* ver
BST的C++实现
吉大秦少游
10-04 1244
BST首先是二叉树，对应的二叉树定义和常用操作封装在以下头文件"bintree.h" // 二叉树的头文件 #ifndef bintree_h #define bintree_h #include <iostream> using namespace std; template<class Elem> struct BinNode{ Elem data; ...
C++ 实现二叉搜索树(BST)
jxhaha的博客
04-20 770
class BST { public: struct Node { int key;//节点的key int value;//节点的value Node* left; Node *right; int N;//节点的叶子节点数目 Node(int _key, int _value, int
avl-tree.rar_avl_avl c++简单_avl tree
09-23
AVL树是一种自平衡二叉查找树（Binary Search Tree, BST），由Georgy Adelson-Velsky和Emanuel Landis在1962年提出，因此得名AVL树，AVL是两位发明者姓名的首字母。这种数据结构在进行插入和删除操作时能保持树的...
BST:C++ 中的 BST
07-08
**C++实现** 在C++中，BST的实现通常使用结构体或类来表示节点，包含键值、左右子节点的指针以及可能的附加信息。通过定义相应的成员函数来实现插入、删除、搜索和遍历等操作。例如，可以创建一个名为`BSTNode`的类...
掌握数据结构：BST树、AVL树及表格的C++实现
C++实现BST树的结构与AVL树类似，也是需要一个节点结构体，区别在于BST树不需要维护高度差，因此不需要实现复杂的旋转操作。BST树的实现包括创建节点、插入节点、查找节点、删除节点等基本操作。 ### 表table 表...
BST与AVL的C++模板实现
昵称一定要靓
04-18 814
C++实现BSTree与AVLTree 回顾树结构时，本打算随便写个
设计C++桌面电话簿软件：BST/AVL树结构实现
项目描述: "本项目为C++实现的桌面电话簿软件，主要采用动态搜索树结构（BST或AVL）来存储和管理联系人信息。联系人信息包括姓名、城市、电话号码等11个字段，支持群组管理、数据的导入导出、以及多种灵活的查询功能...
BST树（二叉查找树）C++的实现
qq_41078889的博客
05-28 1859
二叉查找树（Binary Search Tree），也称二叉搜索树、有序二叉树（ordered binary tree），排序二叉树（orted binary tree），是指一棵空树或者具有下列性质的二叉树： 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值； 任意节点的左、右子树也分别为二叉查找树； ......
二叉搜索树【BST】c++实现
建元的专栏
07-21 527
最近好懒好懒好懒，果然放假就松懈了么..... 数据结构学习到了树，尝试写了下二叉搜索树。 根据算法导论伪代码... 感觉智能指针加进去就是画蛇添足2333333 #include #include #include #include template class Node { public: Node(T *a) :p(NULL), left(NULL),
【C++】实现的二叉搜索树BST
it
07-07 1948
概念： 二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树），二叉搜索树是一种特殊的二叉树 二叉搜索树的性质： 1. 每个节点都有一个作为搜索依据的关键码（key），所有节点的关键码互不相同。 2. 左子树上所有节点的关键码（key）都小于根节点的关键码（key）。 3. 右子树上所有节点的关键码（key）都大于根节点的关键码（key）。 4. 左
算法复习-二叉搜索树BST的c++实现
xchen-lol的博客
04-08 431
#include "my_sorting.h" class BST { private: struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode* fa; TreeNode(int v): val(v), left(0), right(0), fa(0){} ~TreeNode(){co
C++ BST的实现中， 内存分配的情况
a130737的专栏
07-19 1184
关于BST的实现代码， 参见上一个文章， 这里只是贴出代码： // Binary Search Tree - Implemenation in C++ // Simple program to create a BST of integers and search an element in it #include using namespace std; //Definition of
C++数据结构之BST（二叉搜索树）的实现
冰糖雪梨的学习笔记
08-04 797
C++ 二叉搜索树(BST)的实现(非递归版本与递归版本)与应用
最新发布
Wzs040810的博客
12-17 5247
C++ 二叉搜索树(BST)的实现(非递归版本与递归版本)与应用
平衡二叉树（AVL）的实现(详细) c++ 二叉排序树
Tree_sea的博客
07-31 3471
平衡二叉树概念 平衡二叉排序树（Balanced Binary Tree），因由前苏联数学家Adelson-Velskii 和 Landis于1962年首先提出的，所以又称为AVL树。 平衡二叉树是一种特殊的二叉排序树，理解平衡二叉树首先要理解什么是二叉排序树。 如果已经了解二叉排序树可以直接看下面平衡二叉树内容。 二叉排序树（Binary Sort Tree） 所谓二叉排序树(BST)即： （1）若该树的左子树不为空，那么左子树所以结点的值均小于其根结点的值。 （2）若该树的右子树不为空，那么右子树所
二叉搜索树BST的C++实现
liuchenjane的博客
11-05 6537
BST 包含的功能：插入，删除，查找，查找某一结点的后续和前驱，中序遍历和前序遍历 这里，用于实验的二叉树: //二叉搜索树BST #include #include using namespace std; class TreeNode{ public: int key; TreeNode* left; TreeNode* right; TreeNode* p;//
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值