P1311 选择客栈

最新推荐文章于 2025-07-01 18:57:39 发布

_lcj

最新推荐文章于 2025-07-01 18:57:39 发布

阅读量268

点赞数

CC 4.0 BY-SA版权

分类专栏：题解

本文链接：https://blog.youkuaiyun.com/weixin_42404190/article/details/98222251

题解专栏收录该内容

36 篇文章

订阅专栏

本文深入探讨了线段树和ST表两种数据结构在区间最小值查询问题上的应用。通过具体实例，详细介绍了这两种方法的实现过程和代码细节，对比了它们的时间效率，并分享了在洛谷平台上的评测结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目
这道题目写得我真舒畅，一遍过。
由题意可以很轻松的得出这道题目是要查询区间最小值。
众所周知有两种非常普遍的方法；

ST表

线段树

这里要隆重介绍的是线段树，线段树有很良好的性质。就是完全二叉树的一些性质。
如图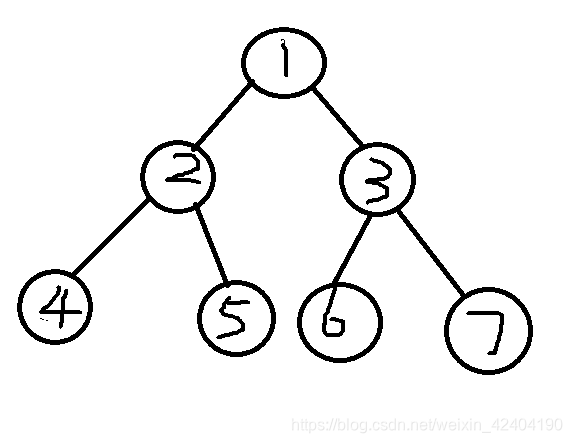
可以观察出左儿子的编号是父节点编号的两倍，右儿子的编号是父节点编号的两倍加一。
这也是线段树要运用的最主要的东西。
分析完该用什么算法后接着来看思路
即判定一个区间的最小值是否小于等于p，若满足条件则答案加一。
接下来上代码

#include<bits/stdc++.h>
using namespace std;
const int ll=2e6+1;
int n,k,p;
int w[ll];
vector <int> e[51];//用于存储相同色调的客栈的编号
struct node{
	int l,r,data;
}t[ll<<2];//线段树4倍存储
void build(int p,int l,int r){
	t[p].l=l; t[p].r=r;
	if(l==r){
		t[p].data=w[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build((p<<1)|1,mid+1,r);
	t[p].data=min(t[p<<1].data,t[(p<<1)|1].data);
}
int ask(int p,int l,int r){
	if(l<=t[p].l&&r>=t[p].r){
		return t[p].data;
	}
	int mid=(t[p].l+t[p].r)/2,ans=1<<30;
	if(l<=mid) ans=min(ans,ask(p<<1,l,r));
	if(r>mid) ans=min(ans,ask((p<<1)|1,l,r));
	return ans;
}
int main(){
	scanf("%d%d%d",&n,&k,&p);
	for(int i=1;i<=n;i++){
		int c;
		scanf("%d%d",&c,&w[i]);
		e[c].push_back(i);
	}
	build(1,1,n);
	int res=0;
	for(int i=0;i<k;i++){
		for(int j=0;j<e[i].size();j++){
			int a=e[i][j];
			for(int x=j+1;x<e[i].size();x++){
				int b=e[i][x];
				if(ask(1,a,b)<=p){
					res+=(e[i].size()-x);
					break;//由于相同色调的客栈的编号在数组中是单调的，所以只要小范围满足，大范围一定满足。
				}				
			}
		}
	}
	cout<<res<<endl;
	return 0;
}

过了几天我决定补上ST表的做法，用洛谷评测了一下时间效率差不多
众所周知ST表可以维护静态区间最值
最大值可以，同理最小值也同样适用
算法流程
1将同样色调的客栈存入一个队列里，
2枚举同样色调客栈的组合方法，用 ST表判定最小费用是否小于p。
这里再不冲一个小技巧
若一个小区间满足条件，那么包含它的区间也一定满足。
上代码

#include<bits/stdc++.h>
using namespace std;
const int ll=2000010;
int n,k,p,f[ll][30],a[ll];
vector<int> v[550];
int ask(int l,int r){
	int k=log(r-l+1)/log(2);
	return min(f[l][k],f[r-(1<<k)+1][k]);	
}
int main(){
	scanf("%d%d%d",&n,&k,&p);
	for(int i=1;i<=n;i++){
		int c;
		scanf("%d%d",&c,&a[i]);
		v[c].push_back(i);		
	}
	for(int i=0;i<k;i++)
		sort(v[i].begin(),v[i].end());
	int t=log(n)/log(2)+1;
	for(int i=1;i<=n;i++) f[i][0]=a[i];
	for(int i=1;i<t;i++)
		for(int j=1;j<n-(1<<i)+1;j++)
			f[j][i]=min(f[j][i-1],f[j+(1<<(i-1))][i-1]);
	int ans=0;
	for(int i=0;i<k;i++)
		for(int j=0;j<v[i].size();j++){
			int x=v[i][j];
			for(int k=j+1;k<v[i].size();k++){
				int y=v[i][k]; 
				int minn=ask(x,y);
				if(minn<=p){
					ans+=v[i].size()-k;		
					break;					
				}				
			}
		}
	printf("%d\n",ans);	
	return 0;
}