路径规划算法—Open Planner学习

最新推荐文章于 2024-11-28 04:51:24 发布

EchoRouRou

最新推荐文章于 2024-11-28 04:51:24 发布

阅读量6k

点赞数 11

分类专栏： Autoware学习文章标签： linux 自动驾驶

本文链接：https://blog.youkuaiyun.com/weixin_42396991/article/details/117418973

版权

Autoware学习专栏收录该内容

2 篇文章

订阅专栏

1.Open planner结构

2.相关工作

2.1 Global planning

2.2 Behavior State machine

5.1 Roll-Out Generation

5.2 Cost Calculation

5.3 Collision Cost

6.总结

1.Open planner结构

2.相关工作

2.1 Global planning

全局规划器，满足最最优函数，并从当前的位置到目标位置的路径，通常使用的是Dijkstra中的距离约束。RNDF文件用于描述了全局路径的信息，比如交通信号灯，车道线等，它是基于的Vector map。

2.2 Behavior State machine

将规划抽象成一组离散的行为

2.3 Local planning

生成很多的Rollouts，Open Planner不需要cost map，只需要矢量地图就能完成全局规划，局部规划和行为状态生成也只需要检测当前位置和检测到的障碍物。

3.系统概述

全局规划器处理路径路由。该算法以矢量地图、起始位置和目标位置为输入，利用动态规划方法寻找最短或最低成本路径。

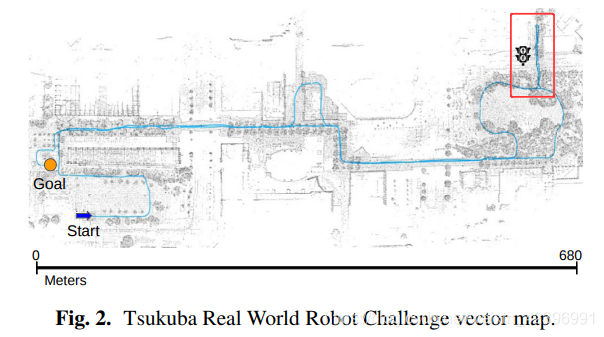
3.1 轨迹生成

Local Path的输入是全局的路径和当前的位置，几个候选轨迹，计算cost，选择cost最近的路径。

4.Global Planner

4.1 Vector map

Open Planner使用2.5D地图，这意味着它包含仅在需要时使用的高程信息。这可以提高规划性能，因为大多数规划是在二维中完成的，但三维信息也可以在极少数情况下使用，例如遇到非常陡峭的斜坡时。

Open Planner，为了加快规划的速度，减少计算量，用了共轭梯度（CG），进行平滑曲线。

4.2 Global Planner

根据驾驶环境的不同，自主车辆规划分为两大类。第一类规划涉及非结构化环境，如越野驾驶或停车时遇到的环境，即我们无法使用矢量地图的位置。这些评估中最合适的映射类型是成本映射。第二类环境包括结构化环境，在这些环境中，我们有明确定义的道路、车道、交叉口等，以及交通标志，所有这些都可以用矢量地图来描述。

4.3 Local Planner

局部轨迹规划器是一组生成平滑轨迹的功能，可通过路径跟踪算法（如纯追踪算法）进行跟踪。对于Open Planner，我们采用了roll-out generation方法（图4），在该方法中，行为生成器可以随时要求重新规划，以生成新的、平滑的roll-out轨迹。下一小节将详细讨论重新规划。

5.Local Planner

5.1 Roll-Out Generation

Roll-Out的部分算法输入是当前位置，规划距离，Roll-Out Numbers，截取的全局路径的下一部分，输出n条平滑的轨迹。图中的Car tip是车辆中心到横向采样点的距离，Car tip的长度决定了在两条轨迹之间切换时转向的平稳性。Roll in是指从Car tip到外部极限的平行横向采样点的距离，这部分的长度和速度成正比。Roll out，从Roll in到局部路径的末端，通过从全局路径垂直移动固定距离来执行直接的横向采样。

局部轨迹规划算法的滚动生成包括三个主要步骤，第一步是利用车辆的当前位置和最大规划距离从全局路径中提取感兴趣的部分。第二步是对新的垂直路径点进行采样，这些点对应于全局路径的扩展部分。采样从横向距离为零的车辆端部边缘开始，然后逐渐增加，以达到使用Roll in末端的每个轨迹指数计算的滚出密度。第三步是使用共轭梯度平滑每个采样轨迹，这是一种非线性迭代优化技术，可消除采样步骤导致的滚动不连续性。这也提高了曲率，从而使转向更平稳。

5.2 Cost Calculation

在避障过程中输入的是Roll out和检测到的障碍物，输出是选定的轨迹。我们使用加性成本函数来评估每个轨迹，它计算三种不同的归一化成本度量，优先级成本、碰撞成本和转移成本，选择其中最小的一个。

5.3 Collision Cost

碰撞成本分两个阶段计算以提高性能。在第一阶段，我们通过测量障碍物轮廓点到每个生成轨迹的距离来测试每个轨迹。由于所有轨迹都与滚入部分之后的中心轨迹平行，因此我们不必在滚入距离之后应用显式测试。障碍物测试是通过“圆内的点”测试来完成的，其中每个轮廓边提供测试点，圆心是路径点，每个圆的半径是车辆宽度的一半加上检测误差。

碰撞成本计算的第二阶段是检查滚入限制后检测到的障碍物与生成轨迹之间的距离。在滚入限制之后，所有生成的轨迹都是平行的，因此我们不需要单独计算每个轨迹的碰撞成本。我们计算检测到的障碍物的轮廓点到中心轨迹的距离，然后使用每个轨迹到中心轨迹的有符号距离来找到每个轨迹的碰撞成本。

6.总结

在本文中，我们解释了我们的方法论、矢量图设计和全局规划器的动态编程。我们还解释了局部规划器如何生成轨迹和安全轨迹选择标准。我们使用状态机转换矩阵概述了行为状态生成，并解释了相关 ROS 节点的功能和用法。我们进行了模拟实验，然后进行了两次实地测试，一次在名古屋大学校园内进行，另一次在筑波真实世界机器人挑战赛中进行。我们的结果表明，OpenPlanner 能够通过复杂的矢量地图规划轨迹并在动态环境中导航，同时处理各种离散行为，例如在停车标志和交通灯处停车以及避开障碍物。如果没有进一步的优化，即使障碍物的折痕数量增加到100个左右，OpenPlanner仍可以以超过10 Hz的速度实时运行。OpenPlanner还可以生成非常平滑的轨迹，从而可以进行更平滑的控制。

本文的主要贡献是将 Open Planner 作为开源资源提供给机器人社区使用和增强。源代码可作为 Autoware 项目中 ROS 包的集合提供。它可以用作独立包或在 Autoware 框架内使用。它可以使用.kml格式的RNDF映射文件（可以轻松创建和修改）以及Autoware支持的矢量映射。 OpenPlanner 的基本功能可作为共享库使用，因此用户可以将其用于 ROS 环境之外的开发。

在这项研究中，我们证明了 OpenPlanner 可以在动态环境中有效和安全地运行，方法是使用改进的电动滑板车成功地通过筑波真实世界机器人挑战赛和在名古屋大学校园内的类似环境中导航。成功的自主导航需要避开移动物体和行人，能够沿着路径跟随移动物体，在狭窄的走廊中导航，通过自动门，以及在红绿灯和停车标志前停车。在我们的现场测试中，OpenPlanner 展示了其执行所有这些任务的能力。

本篇是关于路径规划算法：Open Source Integrated Planner for Autonomous Navigation in Highly Dynamic Environments，所做的一个摘要，在此记录下，只为了方便自己以后阅读。

完！