中国剩余定理学习笔记

前置知识：

• 对于同余方程有了解和余数的各种性质很熟悉。

• 学过求逆元

中国剩余定理，英文 Chinese Remainder Theorem，简称 CRT。

中国剩余定理主要用来解决如下的同余方程：

$$\{\begin{array}{c}x\equiv a_1(\mathrm{mod}{b}_1)\\ x\equiv a_2(\mathrm{mod}{b}_2)\\ x\equiv a_3(\mathrm{mod}{b}_3)\\ \cdot \cdot \cdot \\ x\equiv a_n(\mathrm{mod}{b}_n)\end{array}$$

其中，$b_i$ 两两互质。否则就不能使用中国剩余定理来解决。

可以发现，$x$ 的答案可以有无穷多个。如果 $ans$ 为最小的同时满足所有同余方程的 $x$ 值，则 $ans+{\prod }_{i=1}^n{b}_i\times k$ 也是一个满足要求的答案，$k$ 可以为任意的数。

所以，中国剩余定理是用来求解 $ans$ 值。

---

我们不妨将所有的余数分拆，根据余数的可加性，我们就可以将同余方程拆成几个子同余方程：

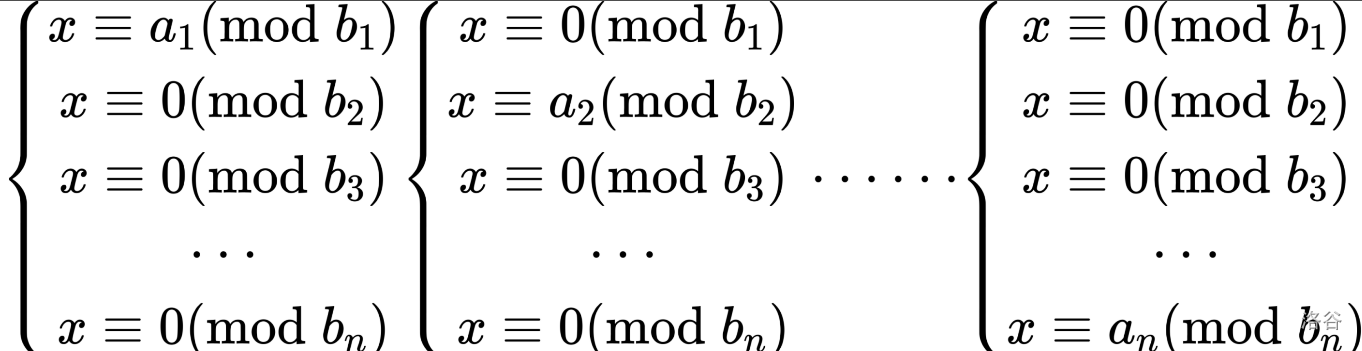
可以注意到这里一共有 $n$ 个同余方程，我们依次求出这 $n$ 个同余方程的解：$an{s}_1,an{s}_2,\cdot \cdot \cdot ,an{s}_n$。

将这 $n$ 个答案加起来，再模上 ${\prod }_{i=1}^n{b}_i$。因为所有的解都是同余的，我们也可以使用任意一个解求出最小的解。

---

但是这样子还是有一些难以计算，不妨再化简一下：

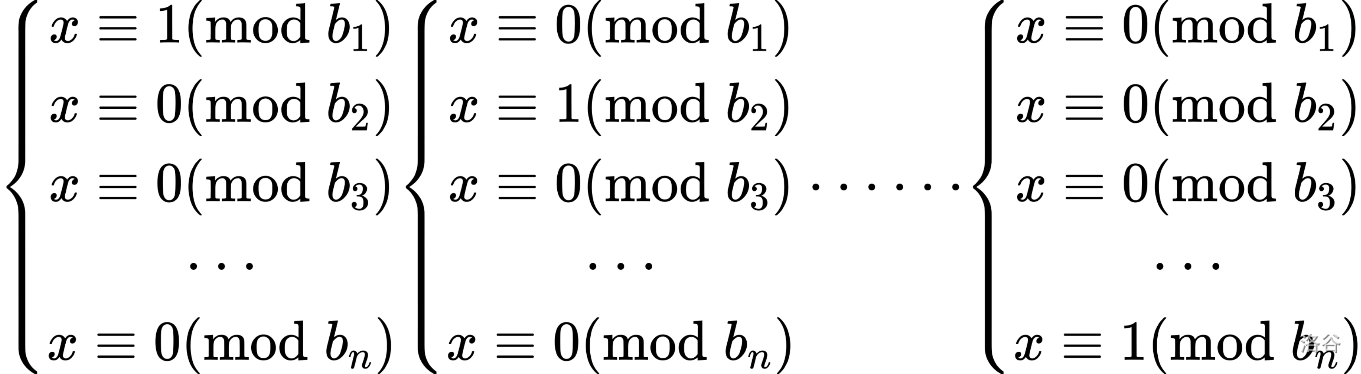
我们依次求出来这几个方程的解：$a{s}_1,a{s}_2,\cdot \cdot \cdot ,a{s}_n$。

则根据余数的可乘性，$\forall i,an{s}_i=a{s}_i\times a_i$。

然后就可以得出答案。

---

注意到所有的方程其实都是差不多的：对于一个 $b_i$ 取余为 $1$，对于剩余的 $b_i$ 都是取余为 $0$。不妨针对其中一个方程来看，方便起见，就选第一个方程。

这时候，我们的问题转化为了求

$$\{\begin{array}{c}x\equiv 1(\mathrm{mod}{b}_1)\\ x\equiv 0(\mathrm{mod}{b}_2)\\ x\equiv 0(\mathrm{mod}{b}_3)\\ \cdot \cdot \cdot \\ x\equiv 0(\mathrm{mod}{b}_n)\end{array}$$

这个方程的解。

不妨针对余数为 $0$ 的部分合并一下。

使用 $m_1$ 记录除了 $b_1$ 以外剩余 $b_i$ 的乘积。

所以就转化成了解决这个方程：

$$\{\begin{array}{c}x\equiv 1(\mathrm{mod}{b}_1)\\ x\equiv 0(\mathrm{mod}{m}_1)\end{array}$$

则对于答案 $as$，有 $as=m_1\times k=b_1\times l+1$。

针对子等式 $m_1\times k=b_1\times l+1$，为了把其中一个恶心的 $l$ 弄掉，不妨转化为同余式 $m_1\times k\equiv 1(\mathrm{mod}{b}_1)$。

然后 $m_1$ 和 $b_1$ 都是可以求出来的定值。

然后你发现了什么？？？发现，$k$ 这东西实际上就是以 $b_1$ 为模数，$m_1$ 的逆元，即 $m^{-1}$。

然后？？？你就可以使用扩展欧几里得做这道题了。

至于 $m_1$ 怎么求，只需要正难则反，使用全体乘积除以 $b_1$ 即可。

其他的如法炮制。

---

模板题：P1495 【模板】中国剩余定理（CRT）/ 曹冲养猪

提示：这道题需要开 __int128！！！

但是 __int128 是没有系统自定义的读入函数的，需要自己手写快读。

这里的 $a,b$ 的位置在输入中反了，注意看清楚题意。

// 使用中国剩余定理（CRT）求解线性同余方程组的代码
#include <bits/stdc++.h>  // 包含常用库
#define int __int128      // 使用128位整数类型处理大数
using namespace std;

int n;                    // 同余方程的数量
const int N = 20;         // 方程最大数量
int a[N], b[N];           // a[i]存储模数，b[i]存储余数
int m = 1;                // 所有模数的乘积（中国剩余定理中的M）

// 读取128位整数（处理输入）
inline int read() {
    char c = getchar();
    int x = 0, s = 1;
    while (c < '0' || c > '9') {
        if (c == '-') s = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9') {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * s;
}

// 输出128位整数（处理输出）
void write(int x) {
    if (x > 9) write(x / 10);  // 递归分解数字
    putchar(x % 10 | 48);      // 输出各位字符
}

// 扩展欧几里得算法：解ax + by = gcd(a,b)，返回gcd，x,y为解
int exgcd(int a, int b, int &x, int &y) {
    if (!b) {
        x = 1, y = 0;
        return a;
    }
    int r = exgcd(b, a % b, x, y);
    int t = x;
    x = y;                      // 更新x
    y = t - a / b * y;          // 更新y
    return r;
}

signed main() {
    n = read();                  // 读取方程数量
    for (int i = 1; i <= n; i++) {
        a[i] = read(), b[i] = read();  // 读取每个方程的模数a和余数b
        m *= a[i];               // 计算所有模数的乘积m
    }
    
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        int k = m / a[i];        // 计算mi = m / a_i
        int x, y;
        exgcd(k, a[i], x, y);    // 求mi模a_i的逆元x
        // 根据CRT累加解：ans += b_i * mi * inv(mi)
        ans = (ans + k * b[i] * x) % m; // 注意取模防止溢出
    }
    // 输出最小正整数解（处理负数情况）
    write((ans % m + m) % m);
    return 0;
}