好久没有更新文科生进阶python系列了,刚好最近和一位粉丝朋友合作进行了一个论文,用到了Python进行统计分析。
我们文科生学Python的一个目标就是要用到科研里,说到科研就需要进行统计分析,SPSS各种不好用,我们学会了万能的Python,替代SPSS实现我们科研论文中的统计分析部分那自然是手拿把掐。
今天用一个最简单的案例,配合脱敏数据例子,讲清楚实验数据进行假设检验的过程,以及Python在其中的作用。本文目录如下:

在此之前,我们需要了解下pingouin库,这个库的名字是企鹅的意思。号称可以搞定各种假设检验和统计模型的Python 库。
官方网址:https://pingouin-stats.org/build/html/index.html
数据猿认为这个库比scipy还好用,值得推荐。
具体的介绍就不赘述了,有兴趣的直接去官方文档查阅。
这里我们先生成一个示例数据,来看看pingouin库的功能——
定量数据分析基础代码:pingouin库和pandas库
1.导入库
importpandasaspd importpingouinaspg
2.创建示例数据集
假设我们有一个包含身高和体重的数据集:
data = {
'Height': [165, 170, 175, 180, 160],
'Weight': [65, 70, 75, 80, 60]
}
df = pd.DataFrame(data)
print(df)
4.计算均值和标准差
使用Pandas计算身高和体重的均值和标准差:
# 计算身高和体重的均值
height_mean = df['Height'].mean()
weight_mean = df['Weight'].mean()
# 计算身高和体重的标准差
height_std = df['Height'].std()
weight_std = df['Weight'].std()
print("身高均值:", height_mean)
print("体重均值:", weight_mean)
print("身高标准差:", height_std)
print("体重标准差:", weight_std)
5. 使用pingouin库进行相关性分析
使用pingouin库计算身高和体重之间的相关性(Pearson相关系数):
# 使用pingouin库计算相关性
correlation_result = pg.corr(x=df['Height'], y=df['Weight'])
print("身高和体重的Pearson相关系数:", correlation_result['r'])
print("相关性显著性(p-value):", correlation_result['p-val'])
6. 使用pingouin库进行假设检验(示例:t检验)
假设我们要比较两组数据(例如男性和女性的体重是否有显著差异):
# 创建示例性别数据
gender = ['男', '男', '男', '女', '女']
df['Gender'] = gender
# 使用pingouin进行t检验
ttest_result = pg.ttest(x=df[df['Gender']=='男']['Weight'], y=df[df['Gender']=='女']['Weight'])
print("男性和女性体重的t检验结果:")
print(ttest_result)
当使用pingouin库进行回归分析、相关系数计算、随机抽样、统计推断和ANOVA分析时,可以按照以下步骤进行操作:
7 .回归分析(Regression Analysis)
假设我们想要分析身高对体重的影响,并进行线性回归分析:
# 使用pingouin进行线性回归分析
regression_result = pg.linear_regression(X=df['Height'], y=df['Weight'])
print("线性回归分析结果:")
print(regression_result)
以下是AI升级后的代码,使用Plotly绘制线性回归分析的图,包含了误差线和区间:
importplotly.graph_objectsasgo importpingouinaspg importpandasaspd # 使用 pingouin 进行线性回归分析 regression_result = pg.linear_regression(X=df['Height'], y=df['Weight']) # 提取回归系数和截距 coef = regression_result['coef'].values[0] intercept = regression_result['intercept'].values[0] # 创建线性回归模型 model_line = coef*df['Height'] +intercept # 创建图表 fig = go.Figure() # 绘制原始数据散点图 fig.add_trace(go.Scatter(x=df['Height'], y=df['Weight'], mode='markers', name='原始数据')) # 绘制线性回归线 fig.add_trace(go.Scatter(x=df['Height'], y=model_line, mode='lines', name='线性回归线')) # 绘制误差线 residuals = df['Weight'] -model_line fig.add_trace(go.Scatter(x=df['Height'], y=residuals, mode='lines', line=dict(dash='dash'), name='误差线')) # 添加区间(可根据需要调整) ci_low = regression_result['CI[2.5%]'].values[0] ci_high = regression_result['CI[97.5%]'].values[0] fig.add_trace(go.Scatter(x=df['Height'], y=model_line+ci_low, mode='lines', line=dict(dash='dot'), name='95%置信区间下界')) fig.add_trace(go.Scatter(x=df['Height'], y=model_line+ci_high, mode='lines', line=dict(dash='dot'), name='95%置信区间上界')) # 设置图表布局和标题 fig.update_layout(title='线性回归分析结果', xaxis_title='身高', yaxis_title='体重') # 显示图表 fig.show()
这段代码使用了Plotly绘制了原始数据散点图、线性回归线、误差线和95%置信区间,帮助可视化线性回归分析结果。
8. 相关系数(Correlation Coefficient)
除了前面提到的Pearson相关系数外,还可以计算Spearman相关系数等其他类型的相关系数:
# 使用pingouin计算Spearman相关系数
spearman_corr = pg.corr(x=df['Height'], y=df['Weight'], method='spearman')
print("身高和体重的Spearman相关系数:", spearman_corr['r'])
9. 随机抽样(Sampling)
使用Pandas进行随机抽样,以抽取示例数据样本为例——
# 使用Pandas进行随机抽样
sample = df.sample(n=3, replace=False) # 抽取3个样本,不放回抽样
print("随机抽样结果:")
print(sample)
10. 统计推断(Statistical Inference)
假设我们想要推断总体的均值是否与样本均值有显著差异:
# 使用pingouin进行单样本t检验
ttest_inference = pg.ttest(df['Height'], mu=170)
print("单样本t检验结果:")
print(ttest_inference)
11. ANOVA分析(Analysis of Variance)
假设我们想要比较不同性别之间的体重是否有显著差异:
# 使用pingouin进行单因素方差分析
anova_result = pg.anova(data=df, dv='Weight', between='Gender')
print("单因素方差分析结果:")
print(anova_result)
12.卡方检验(chi-squared test)
可以分析两个或多个分类变量之间是否存在关联或独立性。例如,研究两种不同治疗方法对疾病治愈率的影响,性别与购买偏好之间的关联等。检验观察频数与期望频数之间的差异。在实际应用中,观察频数是指在一项研究或调查中实际观察到的频数,期望频数是基于某种假设模型(通常是独立性假设)得到的理论预期频数。比较多个分类变量的分布是否相同。例如,在市场调查中比较不同年龄组的购买偏好是否相似。
这里,我们来研究性别和身高、体重之间的是否存在显著性关联。
importpandasaspd
importpingouinaspg
# 数据
data = {
'Height': [165, 170, 175, 180, 160],
'Weight': [65, 70, 75, 80, 60]
}
df = pd.DataFrame(data)
gender = ['男', '男', '男', '女', '女']
df['Gender'] = gender
# 创建身高的分类变量
df['Height_Category'] = pd.cut(df['Height'], bins=[150, 165, 170, 175, 180, 200], labels=['<165', '165-170', '170-175', '175-180', '>180'])
# 执行卡方独立性检验
expected, observed, stats = pg.chi2_independence(df, x='Height_Category', y='Gender')
# 输出结果
chi2_val = stats['chi2'][0]
p_val = stats['pval'][0]
dof = stats['dof'][0]
print("卡方值:", chi2_val)
print("P值:", p_val)
print("自由度:", dof)
# 根据P值做出结论
alpha = 0.05
ifp_val<alpha:
print("在显著性水平0.05下,拒绝原假设,认为身高和性别之间存在显著关联。")
else:
print("在显著性水平0.05下,不拒绝原假设,认为身高和性别之间不存在显著关联。")
上述代码演示了如何使用pingouin库进行回归分析、相关系数计算、随机抽样、统计推断和ANOVA分析。
但是,在实际操作中,我们需要清楚什么数据适合什么样的数据量计算来进行分析。
回到我们的出发点——实验数据的统计分析。
所以,接下来,数据猿就一步步展示,如何将一个包含实验组(男)和对照组(女)的实验数据进行假设检验的。
我们的假设是:
H1:得分在男性组和女性组之间具有显著差异。
H2:男性组得分低于女性组。
实验数据统计分析步骤
话不多说,我们开始实验数据的统计分析。主要是如下步骤:
1.数据导入与清洗- 导入数据并处理缺失值、异常值2.描述性统计- 计算均值、标准差等关键指标3.正态性检验- 验证数据是否符合正态分布4.方差齐性检验- 检查不同组间方差是否齐性5.假设检验- 根据数据特性选择参数检验(如t检验、ANOVA)或非参数检验(如Mann-Whitney U)6.效应量计算- 量化差异大小(如Cohen's d)7.结果可视化- 使用图表直观展示数据分布
1.数据导入与清洗
-
导入数据并处理缺失值、异常值
#过程示例
importpandasaspd
importpingouinaspg
importseabornassns
importmatplotlib.pyplotasplt
# 1. 数据导入
data = pd.read_csv("experiment_data.csv") # 假设数据包含'group'和'score'两列
# 数据清洗
print("缺失值统计:\n", data.isnull().sum())
运行过程截图:
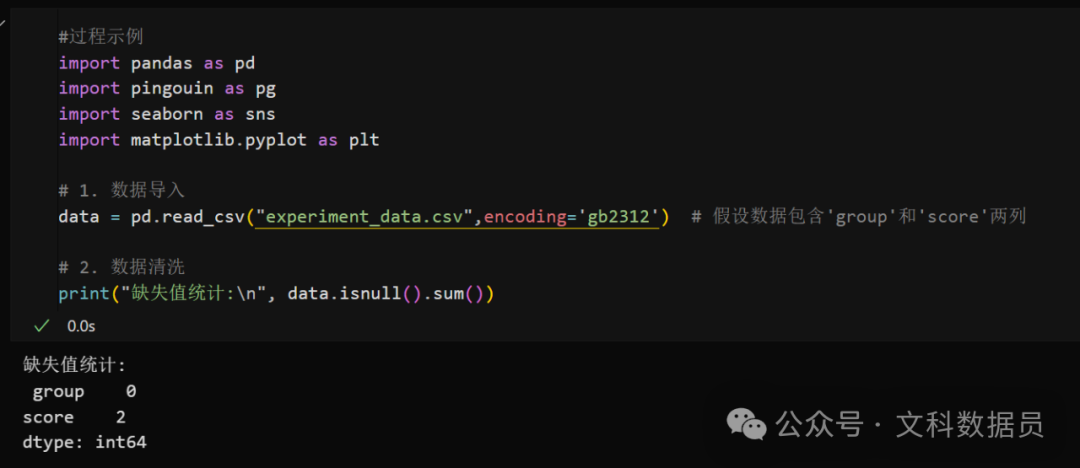
这里先看看我这个示例数据的缺失值,再看看删除缺失值之后的情况。
看原数据内的缺失值位置:
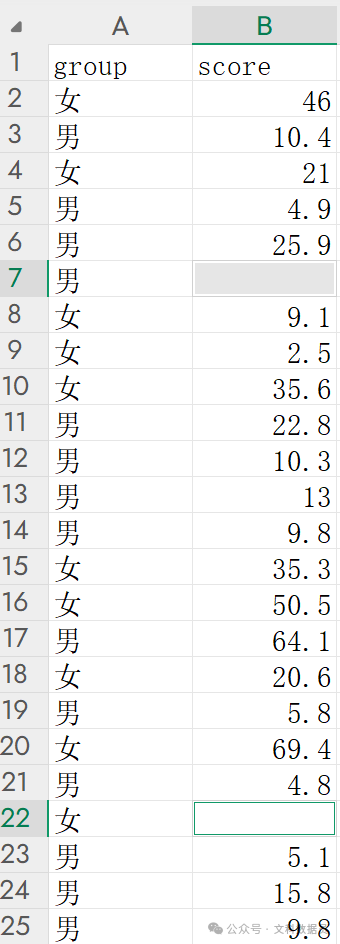
接下来直接删除缺失值。使用df.dropna()函数。
data = data.dropna() # 删除缺失值 data
运行过程截图:
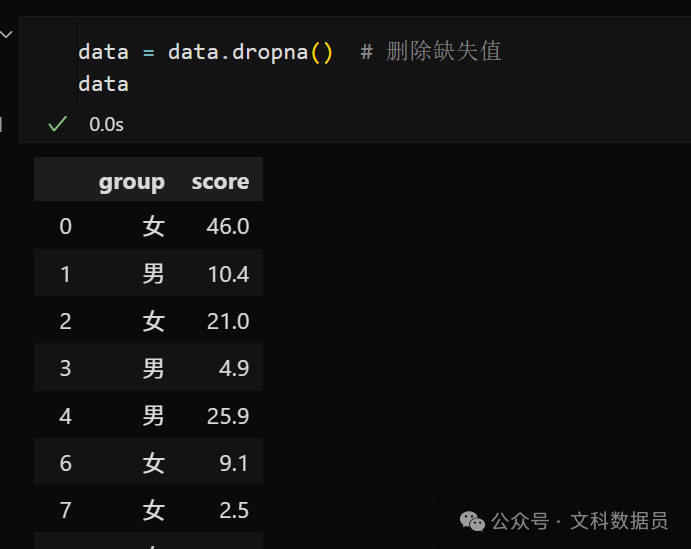
发现,有缺失值的2行数据已经被删除。
当然,这是数据清洗最简单的一种。
有时候,我们还需要统一数据单位,给部分数据补数据等等复杂操作。
可以看看文科数据员的古早文章,看看数据清洗的步骤,此处不再赘述:
2.描述性统计
-
计算均值、标准差等关键指标
\# 2. 描述性统计
desc_stats = data.groupby("group")["score"].describe()
print("\n描述性统计:\n", desc_stats)
describe()函数会计算基本的数据指标。
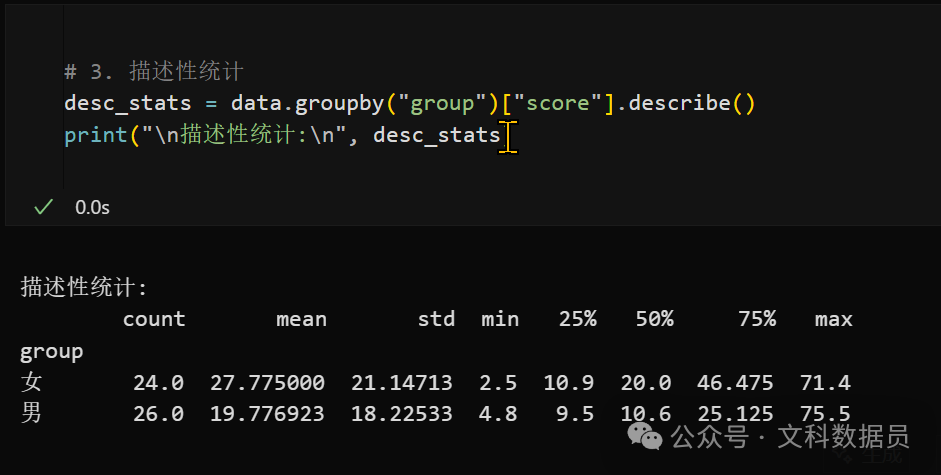
可以发现,describe()函数已经将2个组的频数、平均值、标准差、最小值、三分位、最大值列出来了。
如果需要更多pandas库的操作,可以看往期文章:
文科生进阶python(三)|全面掌握pandas库基础用法
3.正态性检验
-
验证数据是否符合正态分布
# 4. 正态性检验
normality = pg.normality(data, dv="score", group="group")
print("\n正态性检验结果:\n", normality)
在进行假设检验前,需要验证数据是否符合正态分布,不符合的话,有意义的统计量就会比较少,假设检验的方法也较少了。
运行过程截图:
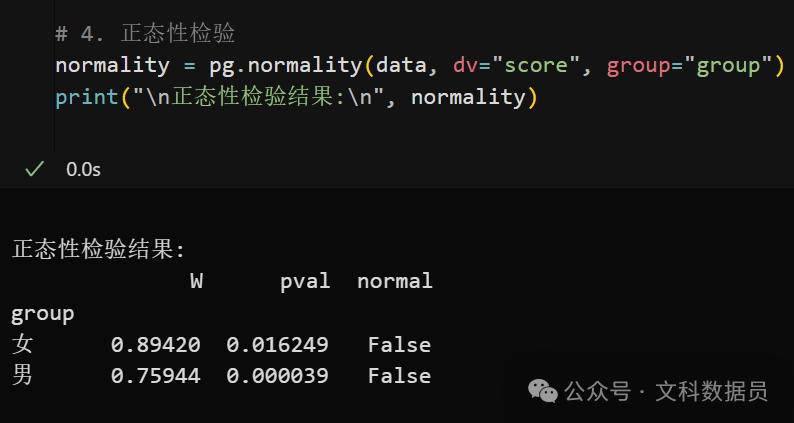
可以发现女性组的Shapiro-Wilk检验统计量W为0.89420,p值为0.016249。通常情况下,如果p值小于显著性水平(如0.05),则拒绝原假设(数据符合正态分布的假设),即认为数据不是正态分布的。
在本例中,p值小于0.05,因此女性组数据不是正态分布。男性组的Shapiro-Wilk检验统计量W为0.75944,p值为0.000039。同样的,p值远小于0.05,因此男性组数据也不是正态分布的。
这里可以强行绘制直方图看看。
男性组:
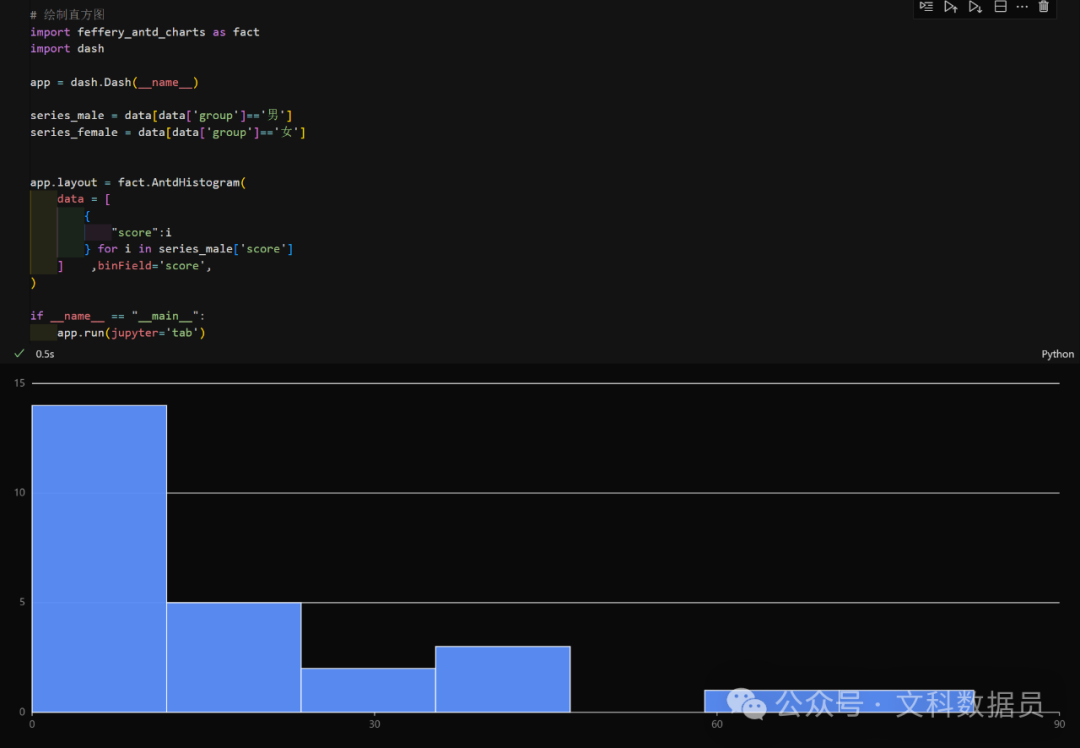
女性组:
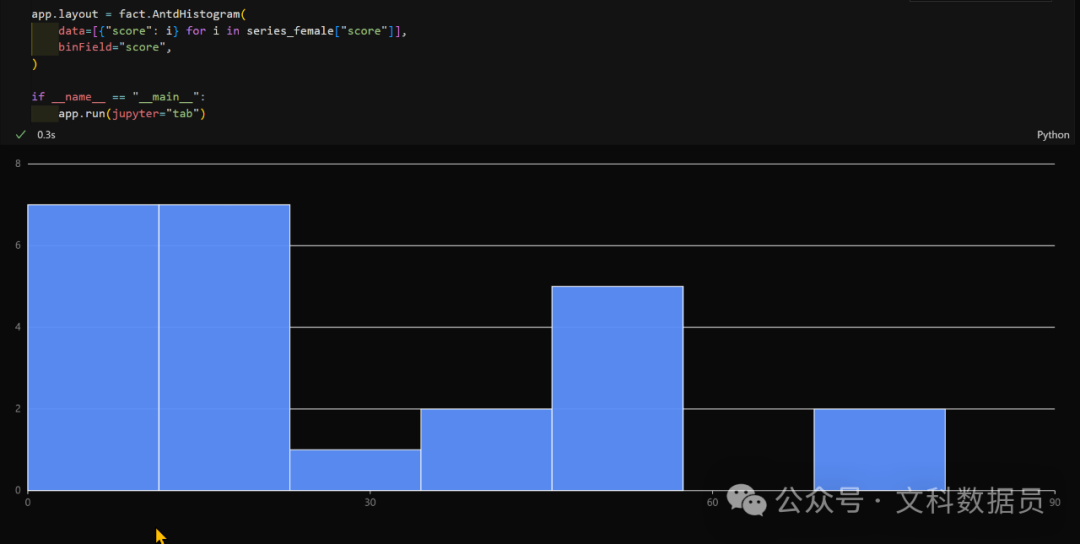
当然,实际操作中,如果计算出了p值不符合正态分布了,那就没必要绘制直方图和核密度图了。
4.方差齐性检验
-
检查不同组间方差是否齐性
# 5. 方差齐性检验(仅用于参数检验)
homogeneity = pg.homoscedasticity(data, dv="score", group="group")
print("\n方差齐性检验结果:\n", homogeneity)
运行过程截图:
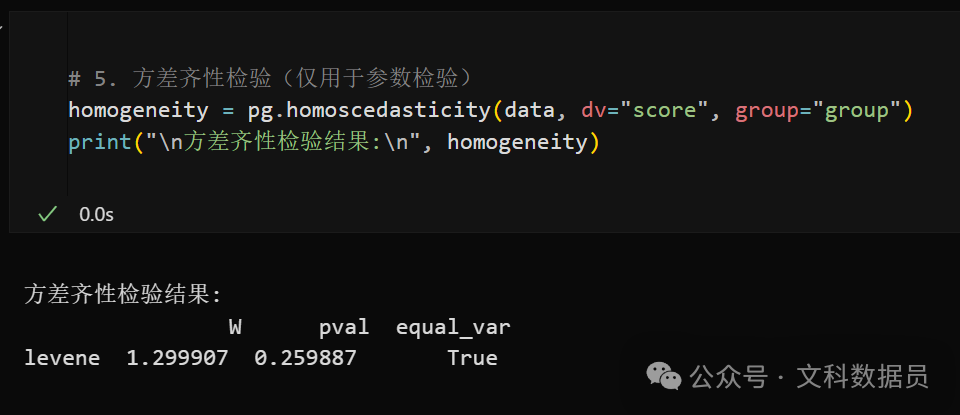
p值 > 0.05(显著性水平通常设为0.05),说明各组数据的方差无显著差异。 可以进行t检验和ANOVA方差分析,但是由于不符合正态分布,谨慎起见还是不采用t检验和ANOVA方差来进行假设检验。
5.假设检验
-
根据数据特性选择参数检验(如t检验、ANOVA)或非参数检验(如Mann-Whitney U)
# 6. 根据检验结果选择假设检验方法
control = data[data["group"] == "control"]["score"]
experiment = data[data["group"] == "experiment"]["score"]
# 如果正态且方差齐性,使用独立样本t检验
ifnormality["normal"].all() andhomogeneity["equal_var"].bool():
ttest = pg.ttest(control, experiment, paired=False)
print("\n独立样本t检验结果:\n", ttest)
# 否则使用Mann-Whitney U检验
else:
mwu = pg.mwu(control, experiment)
print("\nMann-Whitney U检验结果:\n", mwu)
这里我们的数据不符合正态分布,只能用非参数检验。
运行过程截图:
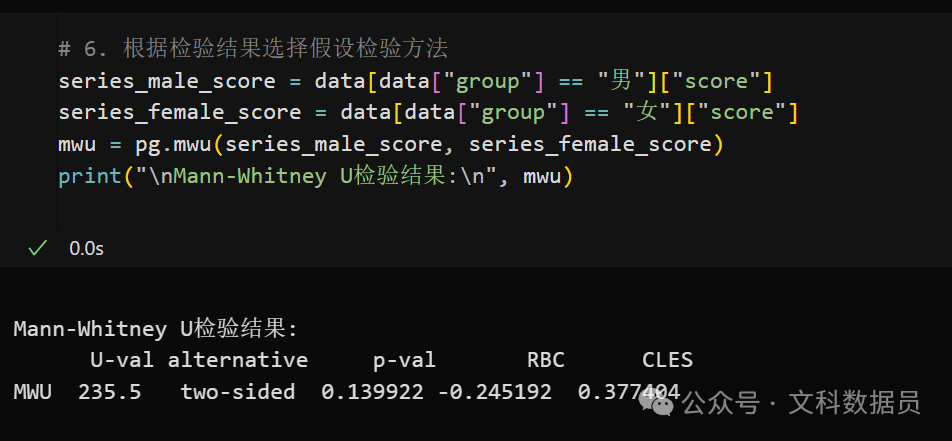
可以发现,p值 > 0.05(0.14 > 0.05),当前数据不支持男与女这2个组存在显著差异,但RBC = -0.245(RBC衡量两组关联方向和强度(范围:-1~1),小到中等效应(Cohen标准:0.1小,0.3中,0.5大)),提示男性组可能存在轻微低于女性组的趋势。
CLES共同语言效应量,这里计算的是男生组大于女生组的概率(范围:0~1)。CLES<0.5,支持男性组更低,但效应微弱(0.377接近中性值0.5)。
6.效应量计算
如果正态分布且方差齐性,就需要计算Cohen's d效应量
注意,这里的数据不符合正态分布,所以到了上述非参数检验,得到了RBC和CLES的值,即可发现统计结论,所以实际操作中无需使用下面的方法。
这里演示下如何计算
-
量化差异大小(如Cohen's d)
# 7. 效应量(例如Cohen's d)
cohend = pg.compute_effsize(control, experiment, eftype="cohen")
print(f"\nCohen's d效应量: {cohend:.2f}")
运行过程截图:
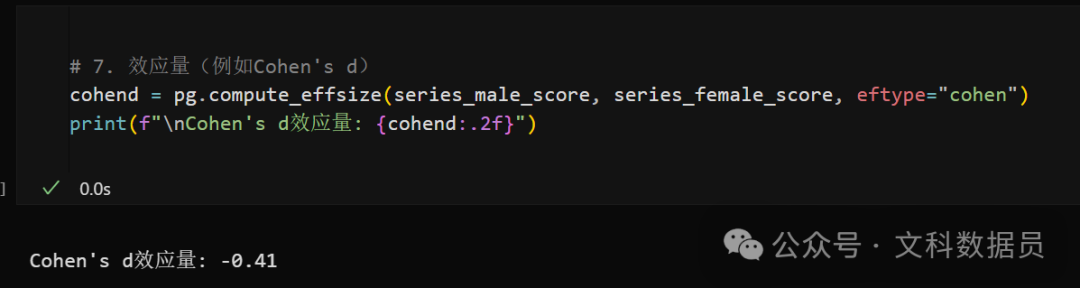
结果为负值(d = -0.41)表示 男性组的均值低于女性组(计算顺序为 男性组 vs 女性组)。
计算公式
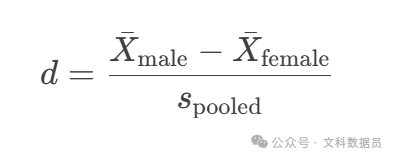
注意:Cohen's d假设数据近似正态分布且方差齐性。若数据严重偏态或方差不齐,建议使用 Hedges' g(小样本校正)或 非参数效应量(如CLES)。
所以,可以理解为女性组平均得分比男性组高(约0.41个标准差)。效应量的实际意义因领域而异。心理学中,|d|=0.4可能被视为有意义。医学中,|d|=0.4可能需结合临床重要性判断。这里|d|=0.41,表明男性组得分略低于女性组,差异为小到中等效应。
7.结果可视化
-
使用图表直观展示数据分布
# 8. 可视化
sns.boxplot(x="group", y="score", data=data)
plt.title("实验组与对照组得分分布")
plt.show()
运行过程截图:
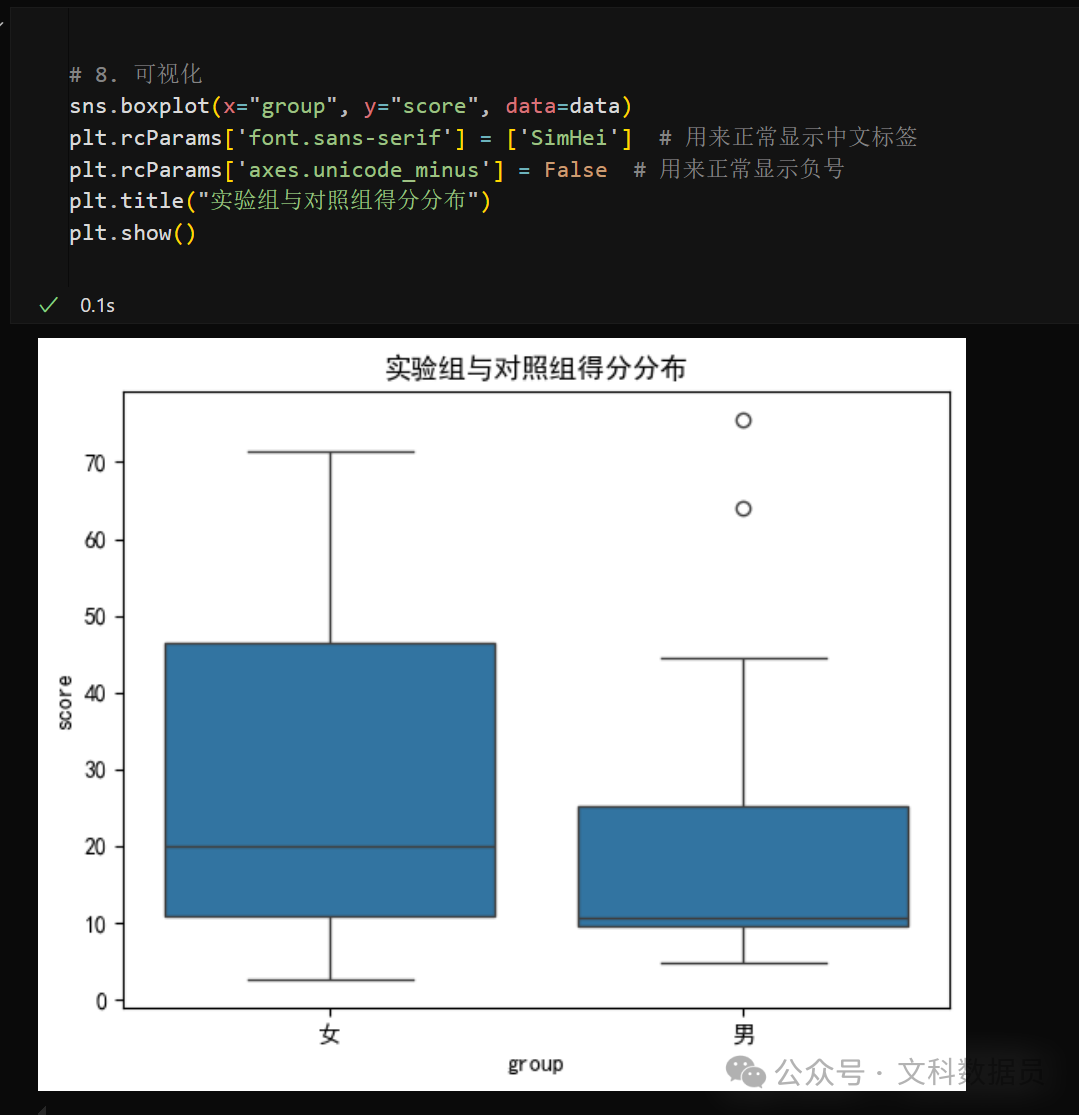
所以,假设H1、H2基本成立。
相关性辅助的情形
除此之外,我们还需要了解下需要相关性分析的情形:
1.如果需要探索性的数据分析,可以先进行探索性分析,如数据可视化、聚类分析、相关性分析等,然后再进行假设检验。
一般需要如下流程:- 数据清洗 → 描述性统计 → 相关性分析 → 根据结果选择假设检验 → 效应量 → 可视化。
2.如果发现其他变量(如年龄、性别)与目标变量显著相关,且可能干扰组间比较,需在假设检验中控制这些变量。
# Python示例(协方差分析ANCOVA): importpingouinaspg # 假设数据包含组别(group)、结果变量(score)、协变量(age) anova_cov = pg.ancova(data=data, dv='score', between='group', covar='age') print(anova_cov)
3.相关性的呈现,可以查看数据猿之前原创的文章:
数据可视化入门(五)|快速制作论文相关性矩阵,并用seaborn库绘制热力图
好的,pingouin库和实验数据的统计分析介绍完毕。
在实际的科研过程中,我们可以根据对数据的理解,让AI写代码帮助我们对数据进行分析。
当然,前提是看过了数据猿的文章,明白统计分析的大概流程,这样才能最大限度发挥Python和AI的作用。需要合作进行科研的,可以后台私信数据猿Riggle。
此外,我们文科数据员乐享群也有不少朋友,可以付费数据分析代做。
如需本文全部代码,请关注文科数据员公众号,在后台回复“实验数据”获取。
欢迎添加数据猿微信(后台回复【0】即可获得微信号)
往期经典文章:
文科生进阶python(六)|CustomTkinter库开发图片管理工具
Python办公自动化(十一) | Dash开发海报自动生成工具




















 485
485

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








