用来处理回归数据_【连载4】：机器学习入门-简单线性回归

目录

1、机器学习简介
2、简单线性回归介绍
3、用Python实现线性回归实例

1、机器学习

机器学习主要是设计和分析一些让计算机可以自动“学习”的算法。而机器学习算法是从数据中自动分析获得规律和模型，并利用规律和模型对未知数据进行预测的算法。

Sklearn (全称 Scikit-Learn) 是基于 Python 语言的机器学习工具，是机器学习中的常用第三方模块。它建立在 NumPy, SciPy, Pandas 和 Matplotlib 之上，里面的 API 的设计非常好，所有对象的接口简单，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。

机器学习的步骤如上的思维导图所示

2、简单线性回归

2.1、定义

线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析，即简单线性回归。

2.2、回归模型和回归方程

回归模型：描述 y 如何依赖于 x 和误差项的方程。简单线性回归模型： y=a+bx+c

回归方程：描述 y 的平均值如何依赖于 x 的方程。简单线性回归方程： y=a+bx

• a--截距
• b--回归系数
• c--误差

2.3、相关性分析

以自变量为x轴，因变量为y轴，用实际数据画出回归方程的散点图，数据点呈直线分布，散点图显示出数据对之间的相关性。

衡量相关性程度的两个因素：

• 1）两个变量的相关性方向，判断正负；
• 2）相关性大小，判断两个变量的相关性程度。

2.4、相关系数

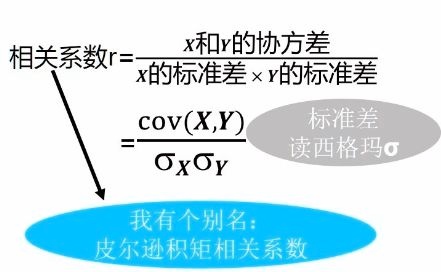
2.5、最小二乘法

用来求出使误差和最小的线性回归方程，即最佳拟合线；

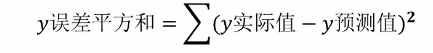
2.6、决定系数R平方

用来评估模型的精确度，即回归线的拟合程度；R平方越高，回归模型越准确；公式：有多少百分比的 y 波动被回归线描述。

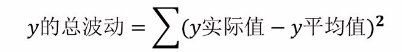
3、用Python实现线性回归实例

3.1、提出问题（特征、标签）
3.2、理解数据（数据导入和查看）
3.3、数据清洗（选择子集、列表重命名、缺失数据处理、数据类型转换、异常值处理）
3.4、构建模型（创建模型、训练模型）
3.5、评估模型（检验模型）

3.1、提出问题

• 学习时长和学习效果的特征和标签有什么相关关系，想用线性回归研究下

分别提取出特征和标签。本示例的特征：学习时间；标签：分数

3.2、理解数据（数据导入和查看）

• 如何导入和建立数据集、选取子集查看情况

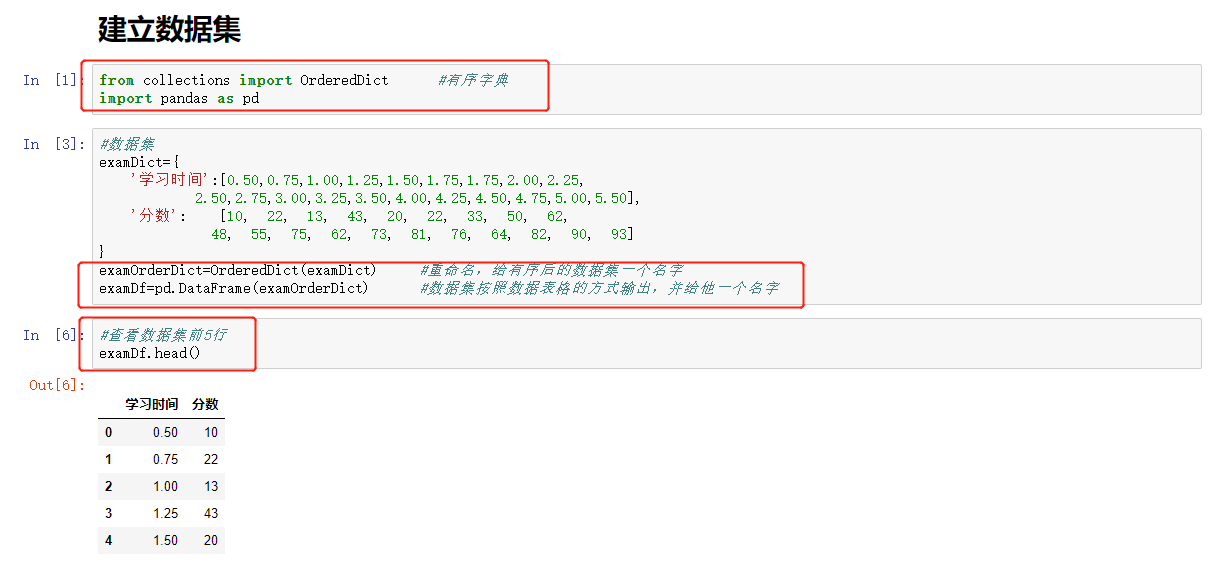
• 如何建立散点图

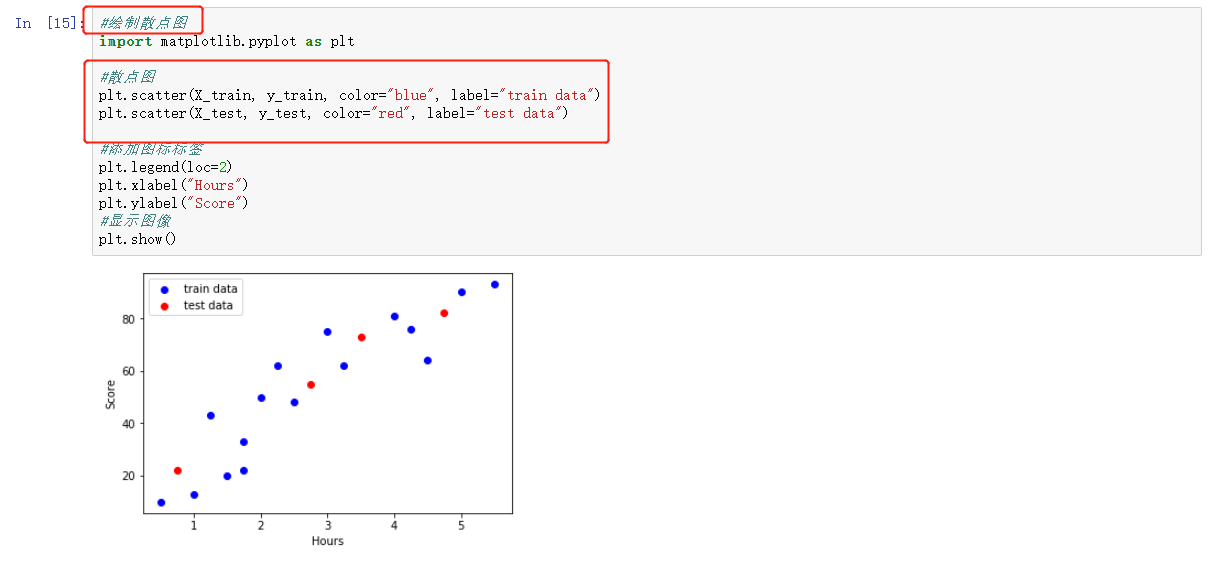
3.3、数据清洗

数据清洗的步骤在连载3中已介绍

3.4、构建模型

• 3.4.1、判断该数据集的两个变量是否复合线性回归模型

绘制数据的散点图，从以上散点图可以初步判断，该数据集特征和标签的关系符合正线性回归模型。

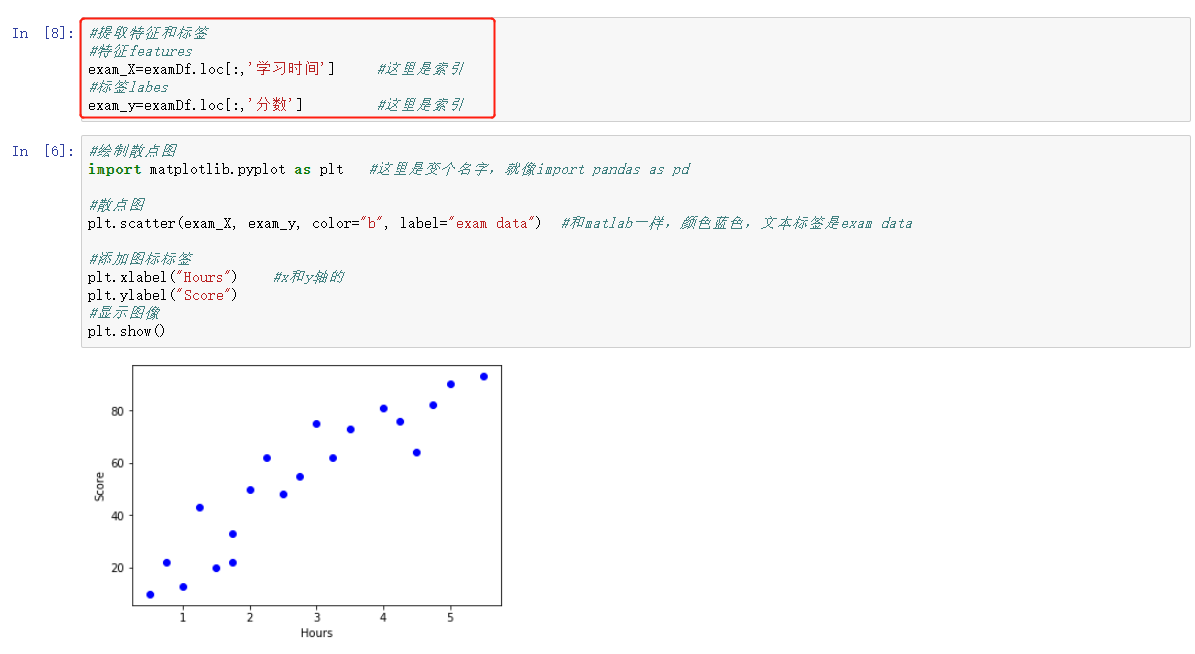
3.4.2、创建模型

• 3.4.2.1、分割数据，将数据随机分成训练数据（80%）和测试数据（20%）

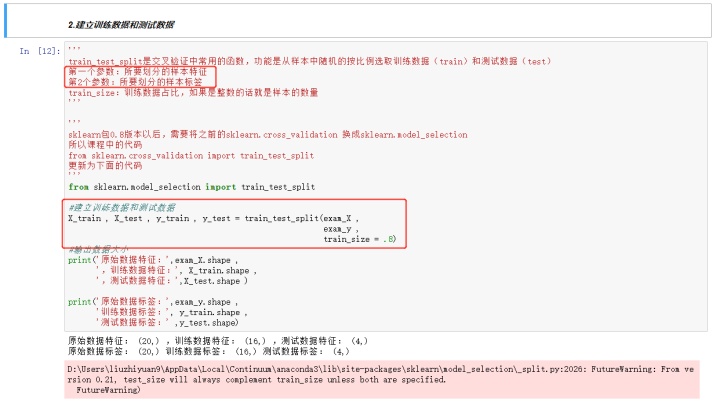
tip：如果数据集只有一个特征，在导入模型前需要用array.reshape(-1,1)来改变数值形状。

• 3.4.2.2、创建模型：线性回归
• 3.4.2.3、训练模型

• 如何查看截距和回归系数？

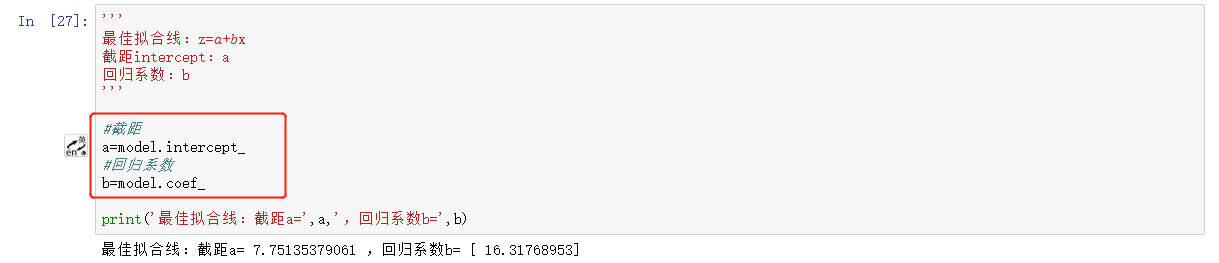
3.5、评估模型（使用测试数据）、

用决定系数R平方评估模型的相关程度。

但是平方误差和（sum of saqured errors）有明显的缺点，就是随着数据量的增加，误差却反而会越来越大；然而事实是，如果数据集越大，那么我们训练得到的模型也就会越接近与实际情况。

1、求出线性回归方程

2、绘制最佳拟合曲线

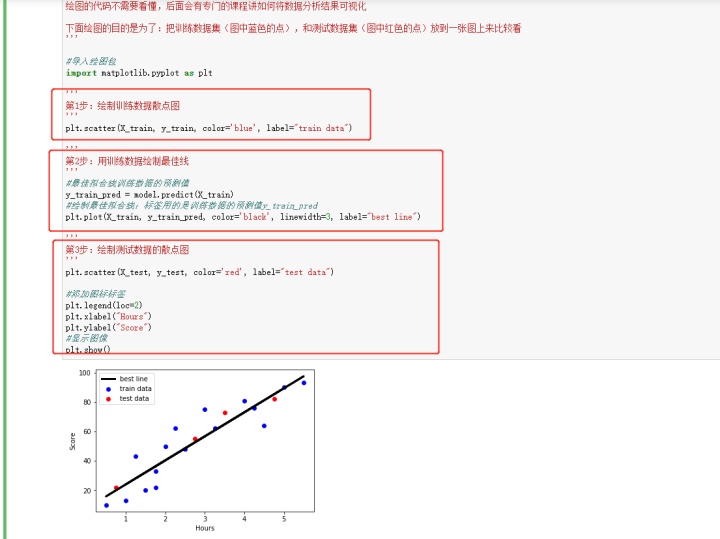
3、判定拟合程度

结论：判定系数 R平方 越接近1，说明模型的拟合度越好。从以上测试数据得出，模型的拟合度大约为0.77，还算可靠。

注意：线性相关关系不等同于因果关系，在实际问题中，例如在社会科学问题中遇到的典型数据，尽管数值低于0.25， 通常也被认为是令人满意的。而在自然科学和生命科学问题中遇到的数据， 经常出现大于或者等于0.60 。事实上，有些情况下我们还能遇到数值大于0.90的情形。