机器学习基本概念

回归：

线性回归：Y=wx+b,y

其中x, y都是已知的参数和label，未知数是w，b，本质是为了求w,b使得对于一个x，就可以预测出一个y

方法：通过loss=（wx+b-y)^2来求解使得loss最小来求得w,b

线性回归就是预测的值是连续的值，逻辑回归只是在线性回归基础上，使用了激活函数，使得y的分布处于【0,1】之间，而x处负无穷到正无穷之间，预测属于某类的概率，属于二分类问题

分类问题：每一个样本的预测值的概率加起来=1，是二分类和多分类问题，而线性回归是二分类问题

数据量：

如果现实世界只有两个数据总量，那给一个数据可以说的过去，但现实世界无穷个量，但给二个数据要预测全部就不现实，根本问题是看要预测的和给的数据量的偏差大小问题

one-hot编码

一、为什么要用做One-hot编码？

在建模过程中，我们通常会碰到各种类型的属性，如果是标称型属性，也就是不具备序列性、不能比较大小的属性，通常我们不能用简单的数值来粗暴替换。因为属性的数值大小会影响到权重矩阵的计算，不存在大小关系的属性，其权重也不应该发生相应的变化，那么我们就需要用到One-hot编码（也有人称独热编码）这种特殊的编码方式了。
二、One-hot编码是什么？

来看一个简单的例子：假设我们有一个特征是自有房和无自有房，样本情况如下：

 data = [['自有房',40,50000],
        ['无自有房',22,13000],
        ['自有房',30,30000]]

    1
    2
    3

编码后的样本矩阵变为：

 data = [[1,0,40,50000],
        [0,1,22,13000],
        [1,0,30,30000]]

    1
    2
    3

也就是说，一个属性如果有N个可取值，它就可以扩充为N个属性，每个样本的这N个属性中，只能有一个为1，表示该样本的该属性属于这个类别，其余扩展属性都为0。

距离

1、欧式距离（欧几里得距离）
欧式距离是最易理解的距离定义，即各坐标点的坐标之差的平方和相加，然后开根号。
二维平面上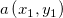点 与点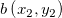 之间的距离公式是：

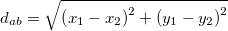
n维空间上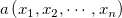点 和点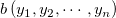 之间的距离公式是：

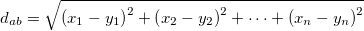
激活函数

1. 什么是激活函数

如下图，在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

2. 为什么要用

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。
如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
 

编码用于对样本label就行分类，距离用于如何计算loss函数，激活函数用于把线性的映射为非线性，同于算Y时，输入输出的计算

预测label

y=f(t) 就是一般的函数形式

y=max f(t) ：y是f(t)函数的最大值

y=argmax f(t) ：y是f(t)函数取到最大值时的参数t

 

比如有 f（t）=t^2 ； t的取值范围{0,1,2}，那么：

y=max f(t)=4；

y=argmax f(t)=2；