正态分布里的西格玛_西格玛和西格玛水平

西格玛和西格玛水平 - Jeff

很多人经常将“西格玛”和“西格玛水平”这两个概念给混淆，在学习六西格玛时，这两个概念必须明确区分开来，并掌握好。

在解释这两个术语之前，先说说正态分布。正态分布(Normal Distribution)概念最早是由德国数学家棣莫弗De Moivre和拉普拉斯Laplace在1733年首次提出，但由于高斯在研究最小二乘法时将正态分布和统计误差结合在一起使用，1809年发表了最小二乘法后，该理论被广泛使用。于是，正态分布也被称为高斯分布(Gauss Distribution)。

[德国马克货币上的高斯头像以及正态分布曲线]

正态分布的特点是对称的钟形曲线，分布的中心位置度由μ决定，分布的宽窄散布程度由σ来决定，同时分布曲线下面总的概率面积为1。

其概率密度函数为:

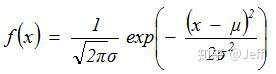
当μ = 0，σ = 1时，正态分布为标准正态分布，其概率密度函数简化为：

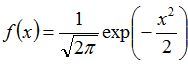
累积概率面积函数为：

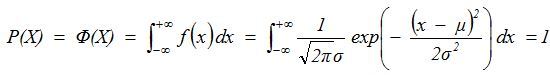
• 西格玛：也即标准偏差，用来衡量一组数据偏离均值程度的统计量，用希腊字符σ来表示，​其计算公式为：

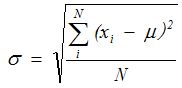
其中：

N ：总体样本数

i ：总体样本序号，i = 1, 2, 3 … N

μ ：总体样本的平均值

如果样本来源总体中的一部分，标准偏差则由s来表示，计算公式为：

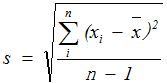
其中：

n ：样本数

i ：样本序号，i = 1, 2, 3 … n

xbar ：样本的平均值

由于样本在取样时，我们都难以取得总体样本的所有数据，都是通过对样本数据进行分析，再以统计推论的手法来对总体分布进行估计和预测。

所以在统计分析中，我们常用的标准偏差估计是按照第二个公式来计算。这公式里还包含了下面四个概念：

1. 平均值Mean (xbar)：数学上称算数平均数（Arithmetic Mean）

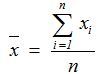
2. 离差Deviation (d)：测量值与均值间的偏差。

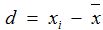
离差是一个很重要的统计偏差量，后期涉及到的模型和残差分析都跟这个有关。

3. 离差平方和Sum of Square (SS)：也叫偏差平方和，大家在做方差分析、回归分析甚至DOE的时候都经常见到的，其计算公式就是，

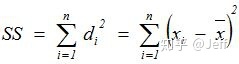
4. 自由度Degree of Freedom (df)：样本中可以自由选择或变化的个数或机会。在这里起到样本计算与总体之间的无偏估计作用。公式是：df = n - 1

听起来有点拗口，我们换一种方式来理解：

地主王老五拿了3个分别是肉馅，白菜馅和没有馅的烧饼出来，打算施舍给甲、乙、丙三个乞丐。地主让甲、乙、丙排着队来挑选，

1. 对于乞丐甲而言，具有选择权，可以从3个烧饼里进行自由选择；当然最后他挑选了肉馅的烧饼。
2. 轮到乞丐乙了，他也是具有选择权的，可以选白菜馅的烧饼或者没有馅；
3. 最后轮到乞丐丙了，他需要做选择吗？不需要了，就剩最后一个烧饼了。
   这里面具有选择的机会次数就是自由度df = 3 – 1 = 2 （甲和乙有选择权）。

• 西格玛水平Sigma Level：过程能力的一种衡量指标，将过程分布的平均值、标准偏差与质量特性的目标值、规格线结合起来。有时也用Z值来表示，

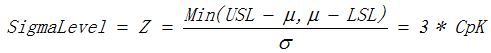
也可以理解为规格线与目标值间的距离最少能容纳k个标准偏差σ，当k = 6时，我们称之为六西格玛水平。

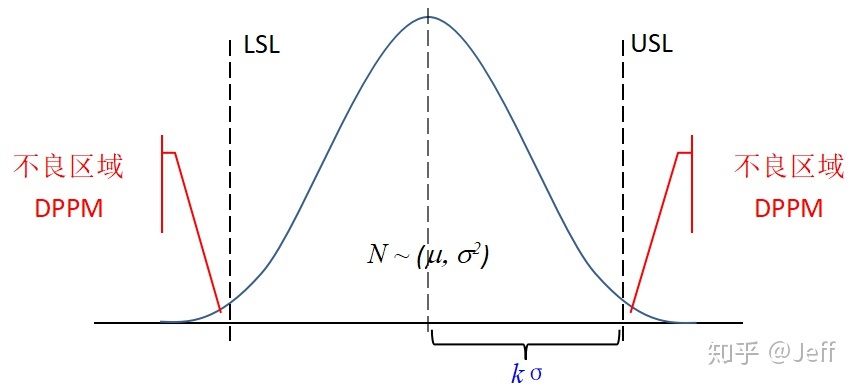
• 在规格线LSL以下的不合格率为：

Excel的计算公式为：=NormDist(LSL, μ ,σ, 1)

• 在规格线USL以上的不合格率为：

Excel的计算公式为：= 1 - NormDist(USL, μ ,σ, 1)

• 在规格线USL与LSL之间区域的累积概率面积为：

Excel的计算公式为：= NormDist(USL, μ ,σ, 1) - NormDist(LSL, μ ,σ, 1)

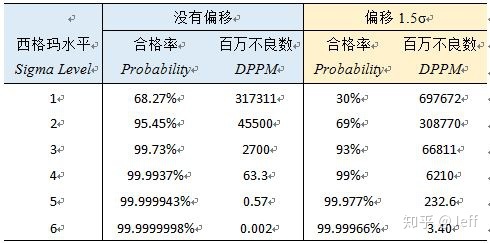
根据上面的公式，我们可以计算出西格玛水平所对应的合格率与DPPM为：

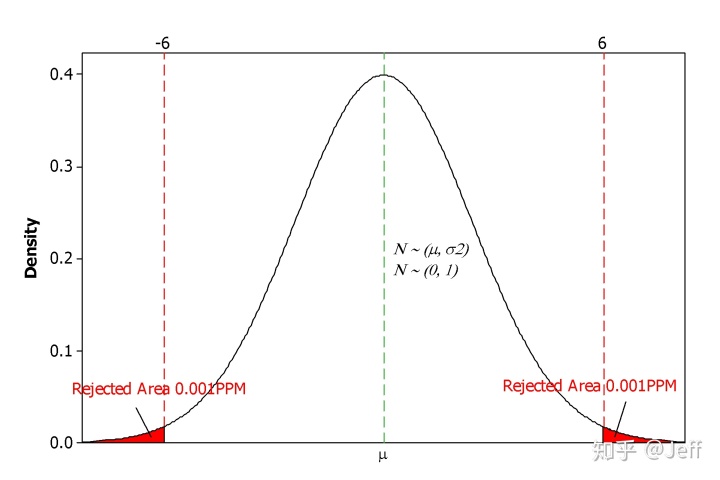
大家可能会说六西格玛能力的过程对应的DPPM不应该是3.4吗？上表其实是在分布没有产生偏移的情况下进行计算的，也就是平均值与目标值重合。但摩托罗拉前辈们的实践总结得出：通常来说，长期数据分布（总体数据）与短期数据分布（样本数据）间存在1.5的σ偏移，或许偏大、或许偏小。也就是说正态分布偏移为N ~ (μ ± 1.5σ, σ2)，下面我们假定偏移为+1.5σ，再来计算一下合格率与DPPM：

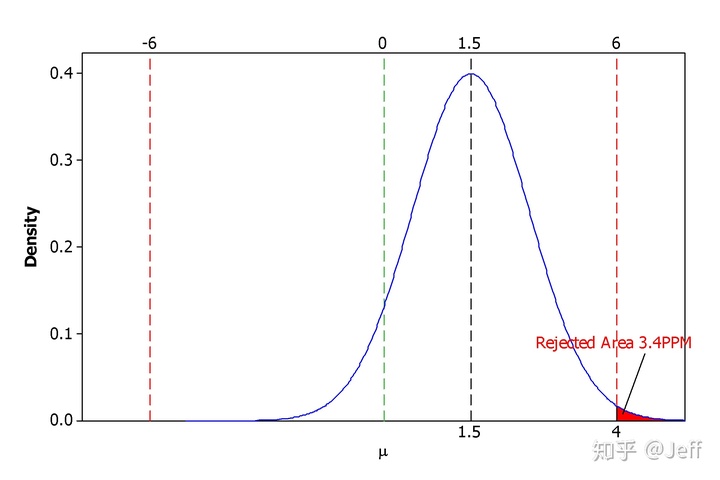
在分布产生1.5σ偏移后，分布左侧在LSL以下的概率就<<0.001PPM，分布右侧超出USL的概率约为3.4PPM，所以总的DPPM值为3.4PPM。

总而言之，西格玛描述的是数据分布的散布程度的统计量；而西格玛水平是过程能力高低水平的衡量指标。

- Jeff整理于2019/11/12

[完]

转载请注明出处，微信公众号：