求均值方差_均值方差组合优化中的效用函数原理分析

在解决均值-方差优化问题时，我们经常要求解以下效用函数最大化：

本文探讨了：1.解均值-方差模型为什么要求解效用函数最大化，2.为什么选择这个形式的效用函数。

1.期望效用理论 在投资决策中，人们面临的核心问题是收益具有不确定性，因此要在收益与风险之间做出权衡。 如果直接计算投资收益的数学期望最大化，虽然可以对一些方案进行优劣比较，但也经常会出现与实际相矛盾的情况。一个典型的例子是“圣彼得堡悖论(St. Petersburg Paradox)”。 “圣彼得堡悖论”是指一个投币游戏：如果第一次投币出现正面，可以得到2元；如果第一次投币出现反面，第二次出现正面，可以得到4元；如果前两次出现反面，第三次出现正面，可以得到8元；以此类推。 该游戏所得收益的数学期望值为：                             但是在实际中，人们肯为这个期望回报为正无穷的游戏支付的费用极低，因此这就存在一个悖论，显然期望收益并不能准确衡量这个投资方案的价值。 数学家Daniel Bernoulli在1738年解决圣彼得堡悖论时，首次提出了期望效用的概念，将期望效用与期望收益进行了区分。他将各种可能下的效用使用概率加权平均，得到期望效用。Bernoulli指出人们在做投资决策时并不是直接基于财富的期望值，而是基于财富带来的效用的期望值，并且财富增加带来的边际效用是递减的。 效用函数将财富值与效用值联系了起来，Bernoulli选择对数函数作为效用函数，即U(w)=ln(w)，其中w为财富。 不考虑初始财富，那么这个投币游戏的期望效用为 即投资者愿意为此游戏支付1.39元。这一计算结果与参与游戏者实际愿意支付的费用较为吻合。 期望效用理论假定投资者会选择使他的期望效用最大化的决策，是解决不确定性投资决策问题的重要判断依据。 2.风险厌恶效用函数  2.1. 风险厌恶的定义 在一次投币游戏中，如果经济个体希望确定性地得到游戏的期望回报，而不想通过参与这次投币游戏获得回报，即确定性收益能给他带来更高的效用，那么我们称这个经济个体是风险厌恶的。 下面使用数学公式来定义。假定经济个体的财富水平为w， ε 是一次投币游戏的收益E( ε )=0，Var( ε )>0，如果有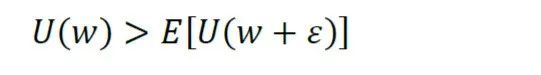： 那么称他为风险厌恶的。 相反，如果有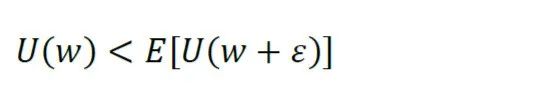： 则称他是风险偏好的。 根据效用函数的定义，更多的财富带来更高的效用，因此效用函数是单调增函数。同时可以证明，如果经济个体是风险厌恶的，那么他的效用函数必然是凹函数；反之亦然。 图 1 凹函数 资料来源：华西证券研究所风险厌恶的效用函数有两个重要性质：