蓝桥杯——剪邮票

剪邮票

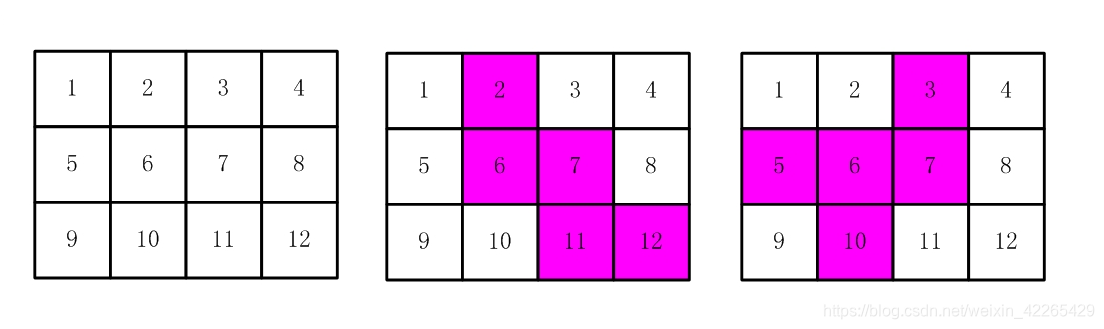
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字

• 观察第一种剪法时，是深度搜索的方法让邮票连成五个格子，但是看第二种剪法时,如果使用深度搜索依次向下时，在数字6的位置就出现了向两个方向走的情况，当邮票形状类似于T时，通过DFS的方法就不能用了。
• 换一种想法，将需要被减下来的邮票设置为数字1，其他为0。 并将这种情况在二维数组中每个情况都表示出来，如果需要全部表示出来的的话可以通过将一维数组全排列后的值传给二维数组，之后判断被剪下来的邮票是否是连通的，成立的话计数加一，将答案输出。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

int Count = 0;
void dfs ( int g[3][4], int i , int j)
{
	g[i][j] = 0;
	if(i + 1 < 3 && g[i+1][j] == 1) dfs(g,i+1,j);
	if(i -1 >= 0 && g[i-1][j] == 1) dfs(g,i-1,j);
	if(j - 1 >= 0 && g[i][j-1] == 1) dfs(g,i,j-1);
	if(j + 1 < 4 && g[i][j+1] == 1) dfs(g,i,j+1);
}

int  fun(int a[])
{
	int g[3][4];
	memset(g,0,sizeof(g));
	// 二维数组赋值
	for( int i = 0;i < 3; i++ )
	{
		for( int j = 0;j<4;j++)
		{
			if (a[i*4+j] == 1)
			{
				g[i][j] = 1;
			}
			else{
				g[i][j] = 0;
			}
		}
	}
	int counts=0;
	for(int i = 0;i < 3; i++ )
	{ 
		for(int j = 0;j < 4; j++)
		{
		    if (g[i][j]==1)
            {
				//检验邮票的连通性，从当前的点向四周扩散，
				//如果邮票是连通的此时这个函数只需要调用一次 返回计数为1。
                dfs(g,i,j);
                counts++;
            }
		}
	}
	return counts == 1;
}
int main(int argc, char *argv[]) {
 	int a[]={0,0,0,0,0,0,0,1,1,1,1,1};
 	do{
		
 		if(fun(a))
 		{
 			Count++;
 		}
 	}while(next_permutation(a,a+12));
 	cout << Count;
	return 0;
}