逻辑回归简介

逻辑回归（logistic regression）也叫对数几率回归，是一种分类算法，而非回归算法。它是通过对数据集进行类似线性回归的计算，得到一个数值，然后对这个数值进行sigmoid运算，将结果映射到(0,1)上的一个概率值，用于判断结果。一般来讲，对大于零的结果判别为类别1，对于小于零的结果判别为类别2。写成表达式就是：

Sigmoid函数定义为：

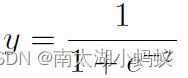
假设线性回归模型：

如果我们用和线性回归一样的方法来衡量预测值和真实值之间的差距，也就是最小二乘法，得到的损失函数是非凸的，要求得最优参数很困难。因此我们采用了对数损失函数作为模型的损失函数，并且这个函数是凸函数，公式如下，这里的θ就是前文的权重w：

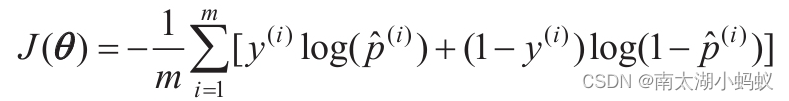
如果直接求这个函数的解析解是不可行的，因为这个函数没有已知的闭式方程来计算最小化损失函数的θ值，不过凸函数的话可以采用梯度下降或梯度上升算法求解。区别在于是逐步下降还是逐步上升。

所谓梯度下降（Gradient Descent）法，是一个一阶最优化算法，通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。因为沿着梯度方向往下走是最快到达底部的方法。所以可以理解为，我们每次都沿着梯度方向往下走一小步，然后衡量误差，然后继续计算当下的梯度，再往下走一小步，如此循环，逐步减少损失函数，直到迭代到规定的次数或者误差到达我们可以忍受的范围内停止。

用公式表示就是：

θ：= θ - α▽θf(θ)，其中α是学习率，也就是每次往下走的快慢程度。▽θf(θ)表示函数对θ求偏导，计算结果如下：

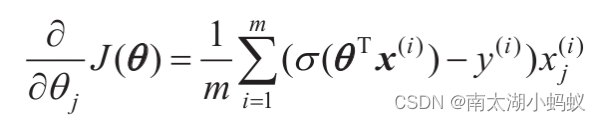
训练过程写成伪代码就是：

每个回归系数初始化为1

重复N次：

        计算整个数据集的梯度

        使用α × 梯度更新回归系数的向量

        （也可以是比较误差，当误差小于一个阈值，停止训练迭代）

返回回归系数

下面我们来做个实验。假设我们从文件中读取一个二分类数据集。

import numpy as np
import pandas as pd

f = open('testSet.txt','r')
data = []
x1 = []
x2 = []
x1_ = []
x2_ = []
y = []
for line in f.readlines():
    if line.split()[2]=='0':
        x1.append(float(line.split()[0]))
        x2.append(float(line.split()[1]))
    elif line.split()[2]=='1':
        x1_.append(float(line.split()[0]))
        x2_.append(float(line.split()[1]))
    data.append([1.0, float(line.split()[0]), float(line.split()[1])])
    y.append(int(line.split()[2]))

分为两种类型，然后画出这两种类型数据的散点图：

import matplotlib.pyplot as plt

plt.scatter(x1,x2,marker='o',c='g')
plt.scatter(x1_,x2_,marker='s',c='r')
plt.show()

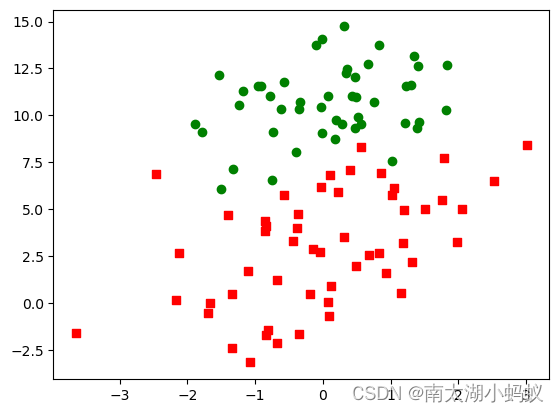
所谓分类，我们要做的就是寻找一条最佳的分割线，把这些数据区分开。

先定义一个sigmoid函数：

def sigmoid(x):
    return 1.0/(1+np.exp(-x))

下面我们执行具体的训练过程：

weights = np.ones((3,1)) # 初始化权重
data = np.mat(data)
y = np.mat(y).T

alpha = 0.003 # 学习率
for i in range(500): # 训练500次
    error = (sigmoid(data*weights)-y)
    #print(error.shape)
    weights = weights - alpha*data.T*error # 更新权重
print(weights)

matrix([[ 6.37778504],
        [ 0.65696184],
        [-0.90352714]])

这就是我们需要的训练后的权重结果，根据这个结果，我们可以画出这条分割线，以区分两类数据。决策边界：y = w0 + w1x1 + w2x2，就是使得函数等于0的地方。

我们从[-3,3]的区间，每个0.1采样一个数字，作为x1，根据决策边界等于0的规则，也就是w0 + w1x1 + w2x2 = 0，在已知w0,w1,w2和x1的前提下，就可以计算出x2，从而画出边界线。

# 画出决策边界
import matplotlib.pyplot as plt

weights = weights.getA() # 训练后返回的weights是矩阵，这里是为了获取他的数组形式
x1_bound = np.arange(-3.0, 3.0, 0.1) # 从-3到3，每隔0.1取一个数字
x2_bound = -(weights[0]+weights[1]*x1_bound)/weights[2] # 根据x1计算出x2
plt.plot(x1_bound, x2_bound)
plt.scatter(x1,x2,marker='o',c='g')
plt.scatter(x1_,x2_,marker='s',c='r')
plt.show()

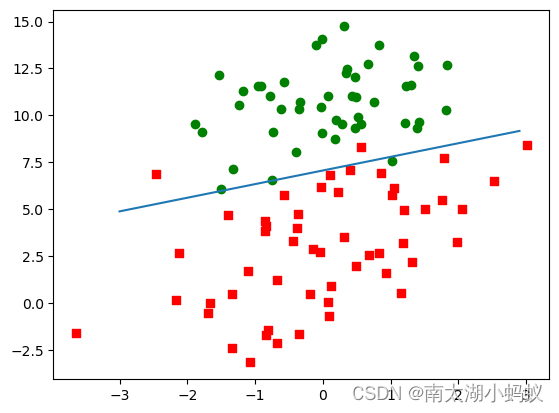
可以看到，数据被比较好的分割开来，只是边界附近的几个样本分类出现了错误，总体精度还是可以的。

当然，如果使用sklearn包的话，会很容易的解决这个问题。

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(fit_intercept=False) # 构建逻辑回归实例，这里的参数代表不考虑截距，仅仅训练出权重
log_reg.fit(data,y) # 执行训练
print(log_reg.coef_)
weights = log_reg.coef_ # 训练出的权重
weights = weights.transpose() # 转置


# 画出决策边界
import matplotlib.pyplot as plt

x1_bound = np.arange(-3.0, 3.0, 0.1) # 从-3到3，每隔0.1取一个数字
x2_bound = -(weights[0]+weights[1]*x1_bound)/weights[2]
plt.plot(x1_bound, x2_bound)
plt.scatter(x1,x2,marker='o',c='g')
plt.scatter(x1_,x2_,marker='s',c='r')
plt.show()

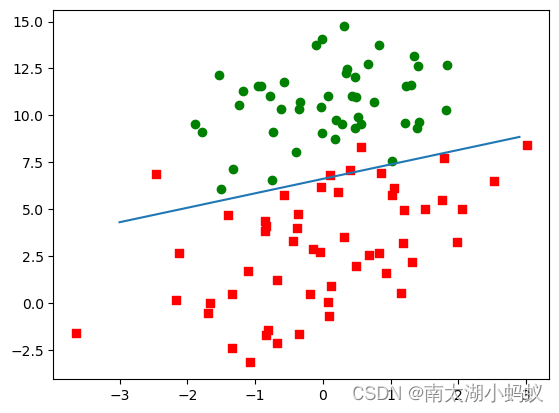
sklearn默认训练100次，可以看到结果也还是不错的。

下面用机器学习领域的经典数据集，鸢尾花数据来验证一下我们的逻辑回归算法的效果。

from sklearn import datasets
iris = datasets.load_iris()
print(list(iris.keys()))
print(iris['target_names'])
print(iris['feature_names'])

['data',
 'target',
 'frame',
 'target_names',
 'DESCR',
 'feature_names',
 'filename']
['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

可以看到，输出数据集的字段描述，并可以可以看到数据集的结果是三种类别的鸢尾花，一共有四个特征。下面开始训练：

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(fit_intercept=False)
log_reg.fit(iris['data'],iris['target'])
x = iris['data']
print(x.shape)
print(log_reg.predict(x[:2,:])) # 预测数据集的前两个样本的标签值
print(log_reg.predict_proba(x[:2,:]))
# 因为LogisticRegression默认是根据数据类别来判别是做二分类还是多分类的，所以根据我们的数据集，结果就是三个类别的概率值
print(log_reg.score(iris['data'],iris['target'])) 

(150, 4)
[0 0]
[[9.81489021e-01 1.85108287e-02 1.50755865e-07]
 [9.53463013e-01 4.65357488e-02 1.23767977e-06]]
0.9666666666666667

可以看出，预测结果的第0列结果最大，两个样本都达到了0.95以上，所以结果预测为第0种类型。训练后的精度达到了96.7%。我们也可以用sklearn自带的工具对训练结果给出详细的评估：

from sklearn import metrics

predict_result = log_reg.predict(x)
print(metrics.classification_report(iris['target'], predict_result))

下表打印出了模型的各项性能指标。

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        50
           1       0.98      0.92      0.95        50
           2       0.92      0.98      0.95        50

    accuracy                           0.97       150
   macro avg       0.97      0.97      0.97       150
weighted avg       0.97      0.97      0.97       150

第二个例子是用逻辑回归实现手写数字识别。手写数字识别作为一个经典例子常用来做深度学习的入门案例，一般是用LeNet来演示，这里我们用逻辑回归来看看效果如何。

from sklearn import datasets
digits = datasets.load_digits() # 加载手写数字数据集
print(list(digits.keys()))
print(digits['images'][0].shape)
print(digits['data'].shape)

['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR']
(8, 8)
(1797, 64)

可以看到手写数字数据集是由1797幅8*8的图像所组成的。

import matplotlib.pyplot as plt

fig = plt.figure()
for i in range(1,11):
    ax = fig.add_subplot(1,10,i)
    ax.imshow(digits['images'][i-1],cmap='gray')

plt.show()

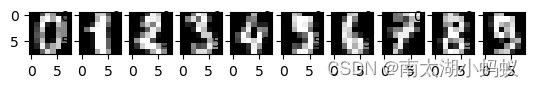
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(fit_intercept=False,max_iter=500)
log_reg.fit(digits['data'],digits['target'])
x0 = x[0].reshape(1,-1)

print(log_reg.predict(x0))
print(log_reg.predict_proba(x0))

[0]
[[9.99999998e-01 5.20247962e-19 5.17359708e-13 4.85235063e-12
  7.55118615e-14 4.22540967e-10 2.28299682e-10 4.41868423e-10
  4.51816361e-10 8.19417517e-11]]

第一个数据的预测结果是0，符合我们的预期，可以看到，打印出的概率值，是0的概率超过了99%。