本文详细介绍了二叉排序树（BST）的概念、插入、删除、查找效率及平衡二叉树（AVL）的原理。通过具体示例和Java代码，深入探讨了平衡旋转操作，包括右单旋转、左单旋转、先左后右旋转和先右后左旋转，以保持树的平衡。
文章目录
1 二叉排序树（BST）
1.1 定义
二叉排序树（Binary Sort Tree），又称二叉查找/搜索树，或是一棵空树，或是具有下列特性的二叉树：
- 若左子树非空，则左子树上所有节点值
都小于根节点的值 - 若右子树非空，则右子树上所有节点值
都大于根节点的值 - 左、右子树也分别是一棵二叉排序树
由此可见，二叉排序树的定义也是递归的。由定义可知，左子树节点值 < 根节点值 < 右子树节点值，因此二叉排序树是中序有序的。
1.2 二叉排序树的插入
二叉排序树作为一种动态树表，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字值等于给定值的结点时再进行插入的。
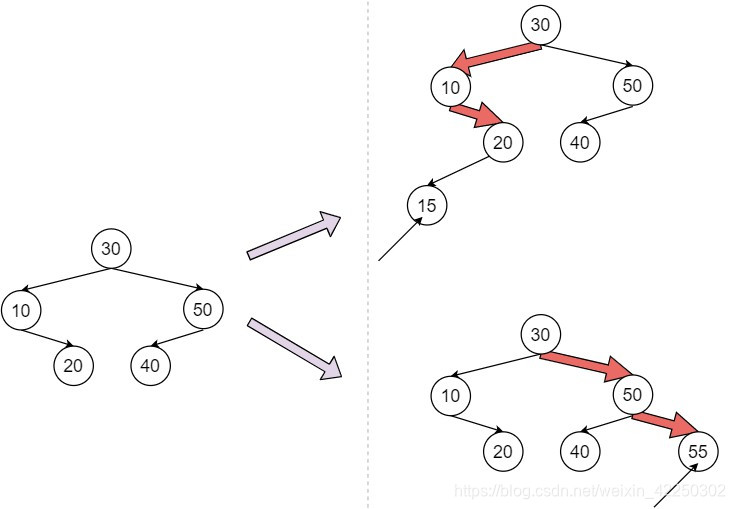
插入结点的过程如下：若原二叉排序树为空，则直接插入结点：否则，若关键字k小于根结点值，则插入到左子树，若关键字k大于根结点值，则插入到右子树。插入的结点一定是一个新添加的叶结点，且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子。
1.2.1 示例java代码
package MyBinaryTree;
public class TreeNode<T> {
public T val;
public TreeNode<T> left;
public TreeNode<T> right;
TreeNode() {
}
public TreeNode(T val) {
this.val = val;
}
public TreeNode(T val, TreeNode<T> left, TreeNode<T> right) {
this.val = val;
this.left = left;
this.right = right;
}
}
package MyBinaryTree;
import java.util.*;
public class SimpleBiTree<T> {
private List<T> levelOrder;
public TreeNode<T> root;
// 从中序序列创建一个二叉树
public SimpleBiTree(List<T> levelOrder) {
// 列表为空或头节点值为空
if (levelOrder.size() == 0 || levelOrder.get(0) == null) {
return;
}
// 根节点赋值
this.root = new TreeNode<>(levelOrder.get(0));
Queue<TreeNode<T>> que = new LinkedList<>();
que.offer(this.root);
int i = 0;
while (!que.isEmpty()) {
TreeNode<T> node = que.poll();
int leftIndex = 2 * i + 1;
int rightIndex = 2 * i + 2;
// 左孩子赋值
if (leftIndex < levelOrder.size() && levelOrder.get(leftIndex) != null) {
node.left = new TreeNode<>(levelOrder.get(leftIndex));
que.offer(node.left);
}
// 右孩子赋值
if (rightIndex < levelOrder.size() && levelOrder.get(rightIndex) != null) {
node.right = new TreeNode<>(levelOrder.get(rightIndex));
que.offer(node.right);
}
i += 1;
}
}
// 返回二叉树非递归中序遍历结果
public List<T> inOrderNonRecursive() {
List<T> res = new ArrayList<>();
if (root == null) return res;
TreeNode<T> node = root;
Deque<TreeNode<T>> stack = new ArrayDeque<>();
while (node != null || !stack.isEmpty()) {
// 向左走到尽头
while (node != null) {
stack.push(node);
node = node.left;
}
// 向右走一步
node = stack.pop();
res.add(node.val);
node = node.right;
}
return res;
}
public TreeNode<Integer> insertIntoBST(TreeNode<Integer> root, int val) {
if (root == null) {
return new TreeNode<Integer>(val);
}
TreeNode<Integer> node = root;
while (node != null) {
if (val > node.val) {
if (node.right == null) {
node.right = new TreeNode<Integer>(val);
break;
}
else {
node = node.right;
}
} else {
if (node.left == null) {
node.left = new TreeNode<Integer>(val);
break;
}
else {
node = node.left;
}
}
}
return root;
}
public static void main(String[] args) {
ArrayList<Integer> levelOrder = new ArrayList<>(Arrays.asList(4, 2, 7, 1, 3));
SimpleBiTree<Integer> tree = new SimpleBiTree<>(levelOrder);
System.out.println("插入前：");
System.out.println(tree.inOrderNonRecursive());
System.out.println("插入后：");
tree.insertIntoBST(tree.root, 5);
System.out.println(tree.inOrderNonRecursive());
}
}
插入前：
[1, 2, 3, 4, 7]
插入后：
[1, 2, 3, 4, 5, 7]
Process finished with exit code 0
1.3 二叉排序树的删除
在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须先把被删除结点从存储二叉排序树的链表上摘下，将因删除结点而断开的二叉链表重新链接起来，同时确保二叉排序树的性质不会丢失。
设要删除的节点为target，节点target的中序遍历前驱节点为predecessor，节点target的中序遍历后继节点为successor。
删除时需考虑4种情况：
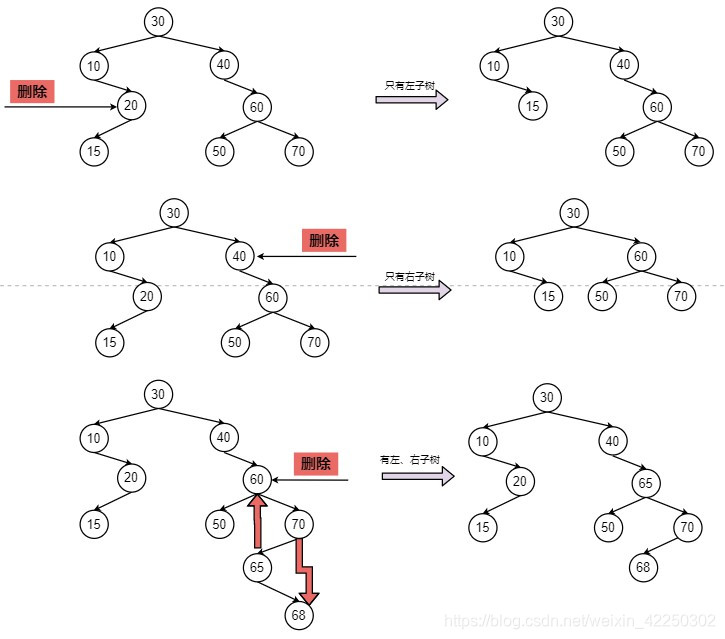
- target是叶结点，则直接删除，不会破坏二叉排序树的性质。
- target只有左子树，则用predecessor替代target。
- target只有右子树，则用successor替代target。
- target有既有左子树，又有右子树。这种情况下，既可以用predecessor替代target，也可以用successor替代target，这样都能保持二叉排序树的性质。为了统一，这里规定：用successor替代target。这样这里第4种情况就转换为了第3种情况。
因此，总结如下：
1、target是叶结点，则直接删除
2、target只有左子树，则用predecessor替代target
3、target有右子树，用successor替代target
1.3.1 示例java代码
package MyBinaryTree;
public class TreeNode<T> {
public T val;
public TreeNode<T> left;
public TreeNode<T> right;
TreeNode() {
}
public TreeNode(T val) {
this.val = val;
}
public TreeNode(T val, TreeNode<T> left, TreeNode<T> right) {
this.val = val;
this.left = left;
this.right = right;
}
}
package MyBinaryTree;
import java.util.*;
public class SimpleBiTree<T> {
private List<T> levelOrder;
public TreeNode<T> root;
// 从中序序列创建一个二叉树
public SimpleBiTree(List<T> levelOrder) {
// 列表为空或头节点值为空
if (levelOrder.size() == 0 || levelOrder.get(0) == null) {
return;
}
// 根节点赋值
this.root = new TreeNode<>(levelOrder.get(0));
Queue<TreeNode<T>> que = new LinkedList<>();
que.offer(this.root);
int i = 0;
while (!que.isEmpty()) {
TreeNode<T> node = que.poll();
int leftIndex = 2 * i + 1;
int rightIndex = 2 * i + 2;
// 左孩子赋值
if (leftIndex < levelOrder.size() && levelOrder.get(leftIndex) != null) {
node.left = new TreeNode<>(levelOrder.get(leftIndex));
que.offer(node.left);
}
// 右孩子赋值
if (rightIndex < levelOrder.size() && levelOrder.get(rightIndex) != null) {
node.right = new TreeNode<>(levelOrder.get(rightIndex));
que.offer(node.right);
}
i += 1;
}
}
// 返回二叉树非递归中序遍历结果
public List<T> inOrderNonRecursive() {
List<T> res = new ArrayList<>();
if (root == null) return res;
TreeNode<T> node = root;
Deque<TreeNode<T>> stack = new ArrayDeque<>();
while (node != null || !stack.isEmpty()) {
// 向左走到尽头
while (node != null) {
stack.push(node);
node = node.left;
}
// 向右走一步
node = stack.pop();
res.add(node.val);
node = node.right;
}
return res;
}
public TreeNode<Integer> deleteNode(TreeNode<Integer> root, int key) {
if (root == null) return null;
// 从右子树删除
if (key > root.val) {
root.right = deleteNode(root.right, key);
}
// 从左子树删除
else if (key < root.val) {
root.left = deleteNode(root.left, key);
}
// 从当前节点删除
else {
// 当前节点是叶节点
if (root.left == null && root.right == null) {
root = null;
}
// 当前节点不是叶节点，且有右孩子
else if (root.right != null) {
root.val = getSuccessor(root);
root.right = deleteNode(root.right, root.val);
}
// 当前节点不是叶节点，无右孩子，有左孩子
else {
root.val = getPredecessor(root);
root.left = deleteNode(root.left, root.val);
}
}
return root;
}
private int getPredecessor(TreeNode<Integer> node) {
node = node.left;
while (node.right != null) node = node.right;
return node.val;
}
private int getSuccessor(TreeNode<Integer> node) {
node = node.right;
while (node.left != null) node = node.left;
return node.val;
}
public static void main(String[] args) {
ArrayList<Integer> levelOrder = new ArrayList<>(Arrays.asList(5, 3, 6, 2, 4, null, 7));
SimpleBiTree<Integer> tree = new SimpleBiTree<>(levelOrder);
System.out.println("删除前：");
System.out.println(tree.inOrderNonRecursive());
System.out.println("删除后：");
tree.deleteNode(tree.root, 3);
System.out.println(tree.inOrderNonRecursive());
}
}
删除前：
[2, 3, 4, 5, 6, 7]
删除后：
[2, 4, 5, 6, 7]
Process finished with exit code 0
1.4 二叉排序树的查找效率
二叉排序树的查找效率主要取决于树的高度。若构造二叉排序树的输入序列越接近有序，则二叉排序树的查找效率越差（因为构造出的二叉排序树的高度越高）。
极端情况下，二叉排序树是一个只有左孩子或右孩子的单支树，此时树的高度最高且等于总结点数，查找性能最差。
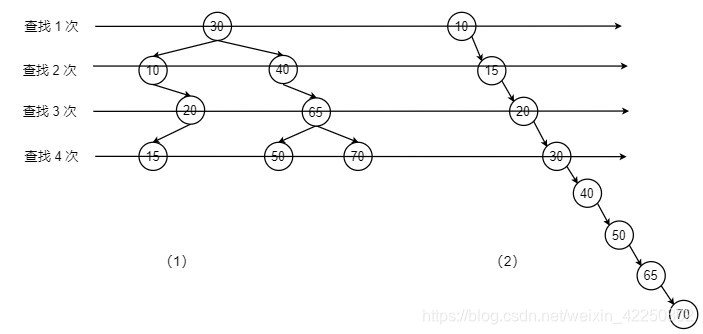
如上图所示，两棵树的平均查找长度为：
A
S
L
(
1
)
=
1
∗
1
+
2
∗
2
+
2
∗
3
+
3
∗
4
8
=
2.25
A
S
L
(
2
)
=
1
+
2
+
3
+
4
+
5
+
6
+
7
+
8
8
=
4.5
ASL_{(1)}=\frac{1*1+2*2+2*3+3*4}{8}=2.25\\ \quad \\ASL_{(2)}=\frac{1+2+3+4+5+6+7+8}{8}=4.5
ASL(1)=81∗1+2∗2+2∗3+3∗4=2.25ASL(2)=81+2+3+4+5+6+7+8=4.5
因此，为避免树的高度增长过快，降低二叉排序树的性能，便提出了平衡二叉树，平衡二叉树的平均查找长度为 O ( l o g 2 n ) O(log_2n) O(log2n)，其中n为节点数。
2 平衡二叉树（AVL）
平衡二叉树（Balanced Binary Tree），为避免树的高度增长过快，降低二叉排序树的性能，规定在插入和删除二叉树节点时，保证节点左、右子树高度差的绝对值不超过1（-1、0、1），将这样的二叉树成为平衡二叉树。又称AVL树，AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。
平衡因子：节点左子树和右子树的高度差，即平衡因子 = 左子树高度 - 右子树高度，则由平衡二叉树定义可知，节点的平衡因子取值只能为-1、0、1。
2.1 平衡二叉树的插入
1 LL平衡旋转（右单旋转）
此种方式在某节点左孩子（L）的左子树（L）上插入新节点，故名为LL型。
如图所示，在节点4的左孩子2的左子树1，插入新节点0。节点4的平衡因子由1变为2（左子树高度增加），故要右旋（高度低的向下去）以平衡子树。
解决方法：
- 节点4右下旋转成为2的右子树（2的右子树被替代，4的左子树变空）
- 节点2的原右子树成为4的左子树（2的原右子树补上4的空左子树）
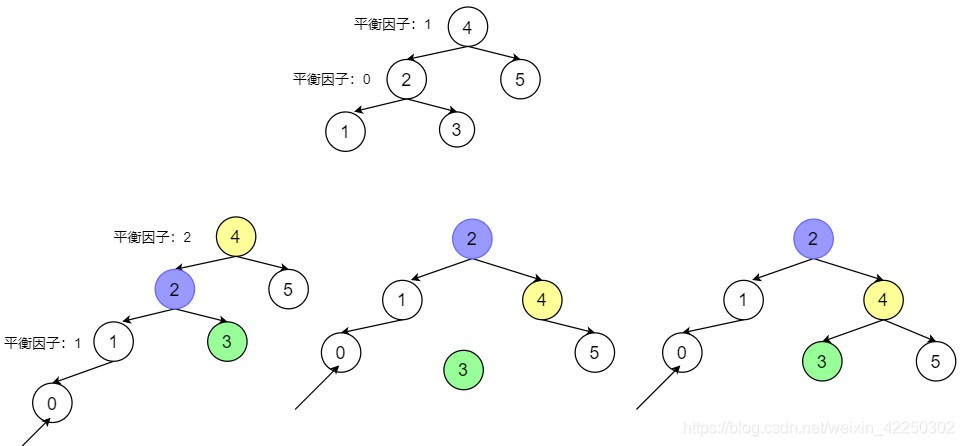
Q：若是在上图中1的右侧插入一个结点又该怎样操作呢？
A：插入在1右侧的节点，同时又在2的左侧（1<新节点值<2），由于是顺序树，则4经过旋转后新节点最终位置仍应在1右侧、2左侧，旋转后节点顺序不变（新节点仍在1右侧、2左侧），所以无论在左侧和右侧插入，操作步骤不变
2 RR平衡旋转（左单旋转）
此种方式在某节点右孩子（R）的右子树（R）上插入新节点，故名为RR型。
如图所示，在节点3的右孩子5的右子树6，插入新节点7。节点3的平衡因子由-1变为-2（右子树高度增加），故要左旋（高度低的向下去）以平衡子树。
解决方法：
- 节点3左下旋转成为5的左子树（5的左子树被替代，3的右子树变空）
- 节点5的原左子树成为3的右子树（5的原左子树补上3的空右子树）
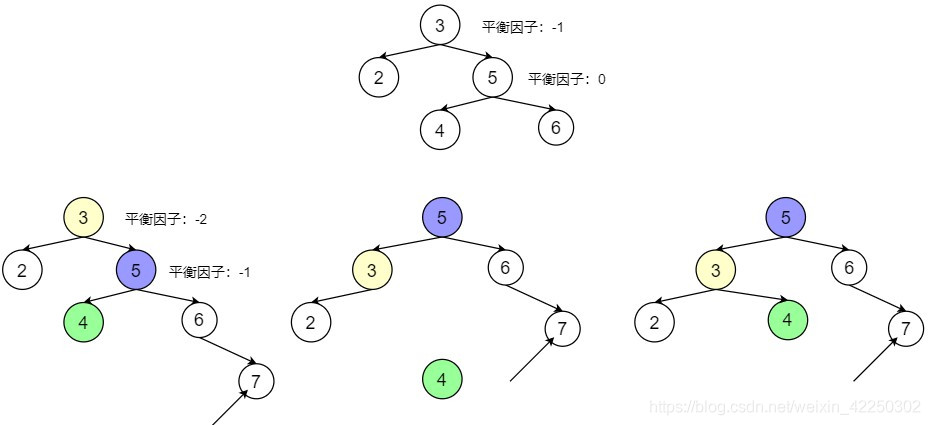
Q：若是在上图中6的左侧插入一个结点又该怎样操作呢？
A：插入在6左侧的节点，同时又在5的右侧（5<新节点值<6），由于是顺序树，则3经过旋转后新节点最终位置仍应在6左侧、5右侧，旋转后节点顺序不变（新节点仍在6左侧、5右侧），所以无论在左侧和右侧插入，操作步骤不变
3 LR平衡旋转（先左旋、后右旋）
此种方式在某节点左孩子（L）的右子树（R）上插入新节点，故名为LR型。
如图所示，在节点6的左孩子2的右子树3，插入新节点4。节点6的平衡因子由1变为2（左子树高度增加），此时需要进行先左后右两次旋转操作。
解决方法：
- 节点6的左孩子2的右子树根节点3
先左上旋转，替代2成为6的左子树，2成为3的左子树 - 节点6
后右下旋转，成为3的右子树（3的右子树被替代，6的左子树变空），再将节点3的原右子树成为6的左子树（3的原右子树补上6的空左子树）
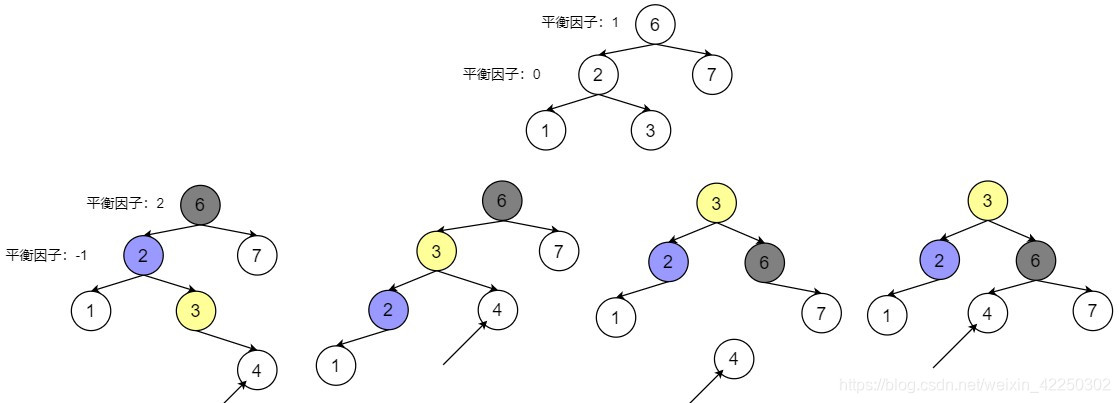
Q：若是在上图中3的左侧插入一个结点又该怎样操作呢？
A：插入在3左侧的节点，同时又在2的右侧（2<新节点值<3），由于是顺序树，则3经过旋转后新节点最终位置仍应在3左侧、2右侧，旋转后3的左子树非空，所以要将节点插入2的右侧，最后将6直接右下旋转即可
4 RL平衡旋转（先右旋、后左旋）
此种方式在某节点右孩子（R）的左子树（L）上插入新节点，故名为RL型。
如图所示，在节点2的右孩子7的左子树6，插入新节点4。节点2的平衡因子由-1变为-2（右子树高度增加），此时需要进行先右后左两次旋转操作。
解决方法：
- 节点2的右孩子7的左子树根节点6
先右上旋转，替代7成为2的右子树，7成为6的右子树 - 节点2
后左下旋转，成为6的左子树（6的左子树被替代，2的右子树变空），再将节点6的原左子树成为2的右子树（6的原左子树补上2的空右子树）
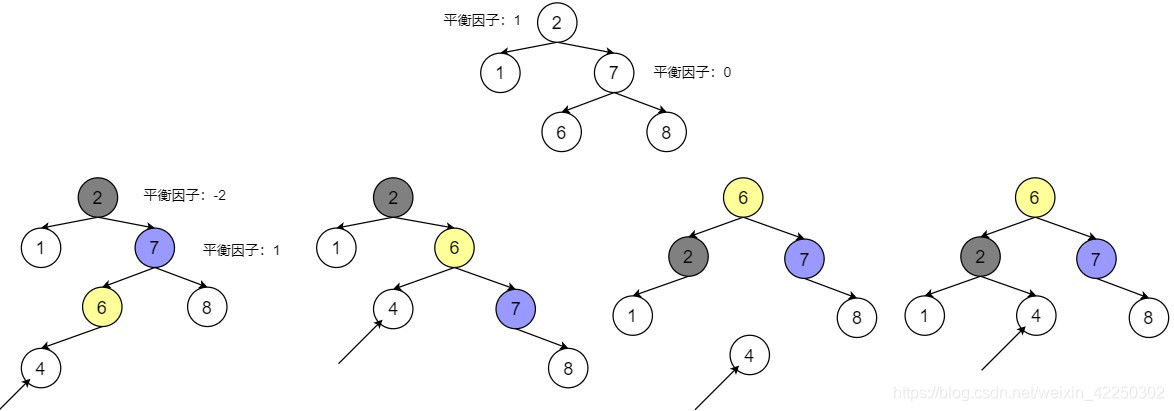
Q：若是在上图中6的右侧插入一个结点又该怎样操作呢？
A：插入在6右侧的节点，同时又在7的左侧（6<新节点值<7），由于是顺序树，则6经过旋转后新节点最终位置仍应在6右侧、7左侧，旋转后6的右子树非空，所以要将节点插入7的左侧，最后将2直接左下旋转即可
扫一扫
2390
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
