KPM算法详解（Next数组）

最新推荐文章于 2024-10-02 16:32:00 发布

没见过凹凸曼

最新推荐文章于 2024-10-02 16:32:00 发布

阅读量1.4k

点赞数

CC 4.0 BY-SA版权

文章标签：算法 java 数据结构

本文链接：https://blog.youkuaiyun.com/weixin_42219387/article/details/116031106

本文探讨了LeetCode_28题中的朴素解法与KMP算法在字符串匹配中的应用。通过对比两种方法，深入解析了KMP算法如何利用Next数组避免重复搜索，提升查找效率。理解Next数组的构建和使用过程对于优化字符串匹配至关重要。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

由LeetCode_28引发的思考
最开始用了剪枝思想的朴素解法虽然做出来了，在看答案的时候发现了有一种叫KMP的算法专门就是解决快速查找匹配串问题的，进行了深入的学习。
下面的图源自@宫水三叶的解答
我们有两个字符串，在原串中寻找是否有匹配串。
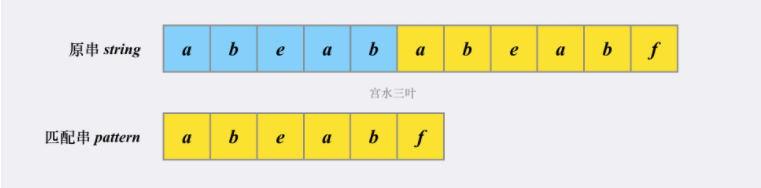
首先我们有两个字符串
先来说说朴素解法：
从匹配串的第一个字符到原串中找，若找到就看第二个是否也相同依次对比，等不相同的话再原串中找下一个与第一个字符相同然后重复之前的操作。
而KPM算法不同的是不再从头匹配，寻找到匹配成功串的最大公共前后缀，将前缀移到后缀位置。
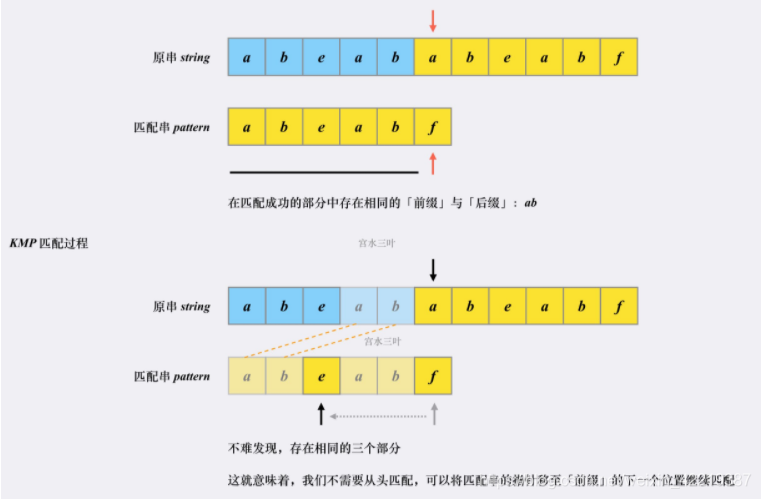
在这里插入图片描述
然后我们的目标就是得到匹配串中的最长前后缀，这时就要引入Next数组，网上有很多计算next数组的方法，我这里找到一个最容易理解的。
next数组中的内容为到该位置的子串的相同前后缀的数量
eg aabaabaa 对应的next数组应该为 01012123
设两个指针i,j

       int j=0;
       for(int i=1;i<len_ned;i++){
           while(j>0 && ned[j]!=ned[i]){
               j = next[j-1];
           }
           if(ned[i]==ned[j]){
               j++;         
           }
           next[i] = j;
       }

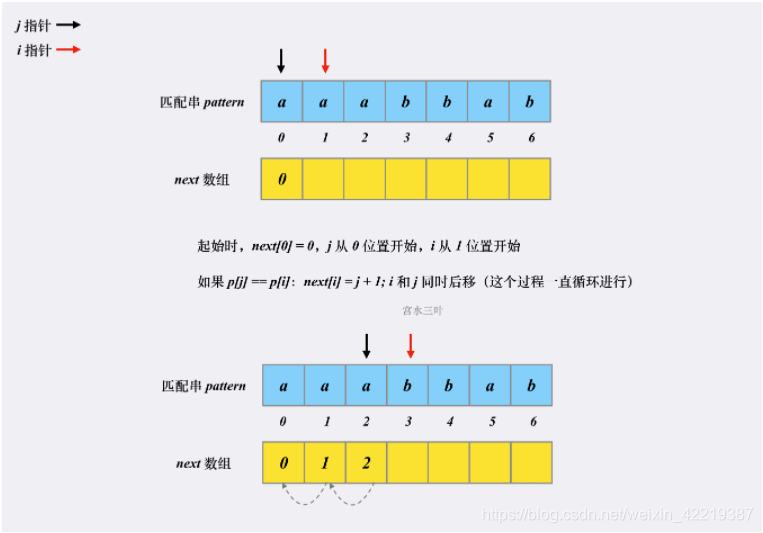
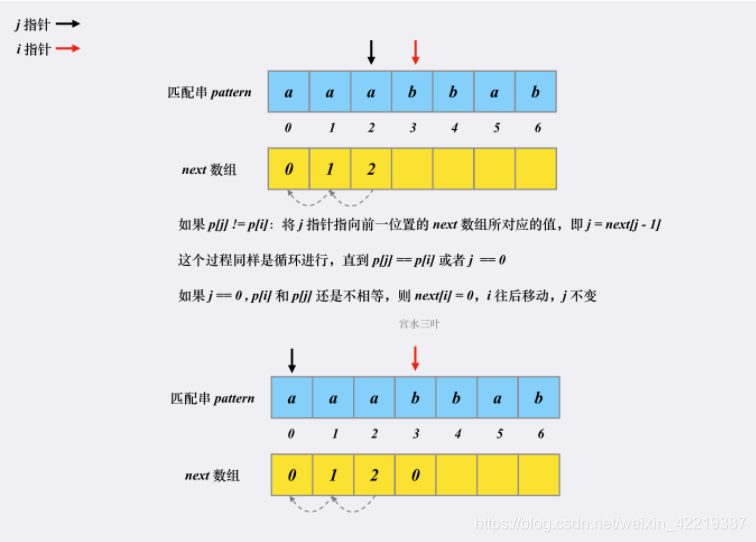
在这里插入图片描述
代码和图不太一样理解一下。j++的顺序不太一样。重点是字符不相同时j=next[j-1]
得到next数组
再开始比较字符串

       j=0;
       for(int i=0;i<len_hay;i++){
           while(j>0 && ned[j]!=hay[i]){
               j = next[j-1];
           }
           if(ned[j]==hay[i]){
               j++;
           }
           if(j==len_ned) return i-j+1;
       }