目标检测---批归一化（BN）原理与细节详解

目标检测—批归一化（BN）原理与细节详解

问：为什么会出现BN这种操作？

答：假设我们现在有四个样本，每个样本有四个特征，每一个神经元可以代表一个特征（这句话我是在网上找到的，感觉有点道理，但是我又找不出来哪有道理~~），这些数据作为输入传进BP网络（假设就是为简单的感知器模型）中，可以得到一下损失函数，通过这个损失函数可以很明显的看到，如果随着w的更新，当w4的取值大小发生一点点的改变，那么整个loss就会发生相应的很大的变换，这是因为第四个特征对于该模型来说权重太大，所以为了避免这种情况出现，BN就来咯~

再举一个例子~~~

整个图也可以很明显的说明BN对损失最小化的作用，左图是没有做批归一化操作，是一个椭圆形的；右图是做了批归一化操作，是一个等高圆。
在神经网络的训练过程中，我们一般会将输入样本的特征进行标准化处理，使数据变成均值为0，标准差为1的高斯分布，或者范围在0附近的分布。因为如果数据没有进行该处理的话，由于样本特征分布比较散，可能会导致学习速度慢甚至难以学习。

BN到底是什么，它的操作步骤是什么样的？

概念：BN其实就是将神经元的输入进行一个方差为0，均值为1的高斯分布转换，再将其进行平移与缩放。
目的：其实上面已经说过了，就是希望样本的特征分布比较有规律，便于参数的更新和模型的收敛。
使用的位置：论文中建议放到卷积层/FC层后，激励层/池化层前，而实际应用的时候有时候会放到激励层后。
步骤：

• 1. 求解每个训练批次数据的均值
• 2. 求解每个训练批次数据的方差
• 3. 使用求得的均值和方差对该批次的数据做标准化处理，获得0-1分布。
• 4. 尺度变换和偏移：使用标准化之后的x乘以γ调整数值大小，再加上β增加偏移后得到输出值y。这个γ是尺度因子，β是平移因子，属于BN的核心精髓，由于标准化后的x基本会被限制在正态分布下，会使得网络的表达能力下降，为了解决这个问题，引入两个模型参数γ、β进行平移变化。
举个例子：

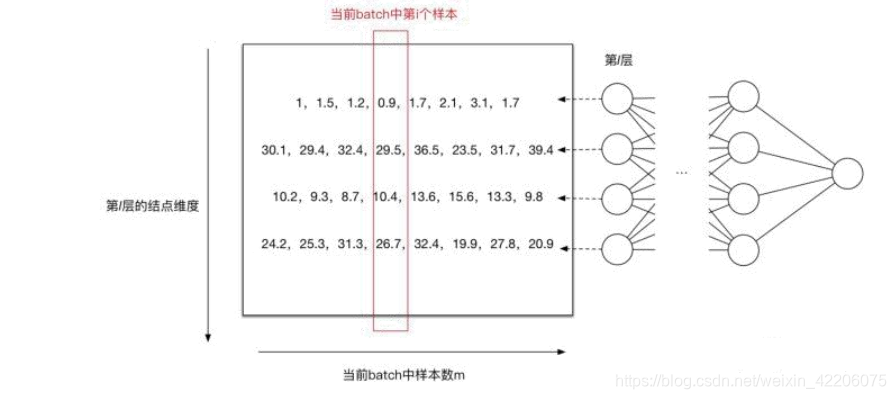
上图中一共有8个样本，每个样本有4个特征，那么画红款的就代表当前batch中第几个样本，每一行代表所有样本中第几个特征的汇总。
第一个神经元均值为1.65，方差为0.44，ε为1e-8（***不是按照红框进行高斯分布转换，是按照每一行进行转换！！！！***）
经过BN之后得到下图所示：

在上面，我着重标记了第四步，是因为其实我个人认为这一步才是BN的核心，也是为什么BN能够应用广泛的原因，下面好好讲讲这一步：

一般来说，FC层之后会接一个BN的操作，然后再接一个激活函数，上面是激活函数sigmoid，在经过BN（假设这里没有用尺度变换和偏移）之后，数据分布呈现在-1~1之间，在这范围中，sigmoid函数基本上是线性的，所以丧失了激活函数的非线性的作用，再举一个激活函数的例子

上面是relu激活函数，当输入的数据在-1~0之间的时候，此时的数据全部都会进行激活成0，就会导致部分的特征没有学到。
综上所述，在经过高斯分布转换之后，一定要做一个尺度变换和偏移~

上图3其实就是经过最后一步得到的最终的BN结果。尺度变换的过程中，两个参数β和γ也是相当于变量，随着反向传播的时候进行更新，说白了，就是误差对β和γ进行求导，然后进行更新~

在卷积中的BN

在CNN中，由于CNN的特征是对应到一个feature map特征图上的，所以在CNN中做BN的时候不是以神经元作为单位，而是以feature map特征图作为单位的。也就是针对一个批次中的一个channel的所有feature map计算一对参数γ、β。（如下图所示，分别有两个3维channels的图像，两张图中相对应的维度进行BN操作）这样可以减少模型参数的数目。假设现在batch_size=8，feature map的大小为32 * 32，feature map数量为10个，传统的BN参数量为: 20480。因为卷积核中每个位置就是一个神经元。

BN的好处与坏处

好处：

• 梯度传递(计算)更加顺畅，不容易导致神经元饱和（防止梯度消失(梯度弥散)/梯度爆炸，允许使用饱和性激活函数eg:sigmoid、tanh等） • 学习率可以设置的大一点，加快训练速度。
• 对于模型参数的初始化方式和模型参数取值不太敏感，使得网络学习更加稳定，提高模型训练精度。
• 具有一定的正则化效果，类似Dropout、L1、L2等正则化的效果。

坏处：

• 如果网络层次比较深，加BN层的话，可能会导致模型训练速度很慢。
• 训练批次不能设置太小，一般建议批次大小16以上。

Tensorflow实现BN代码

https://blog.youkuaiyun.com/huitailangyz/article/details/85015611