7-5 拓扑排序

1.用一个有向图表示一个工程的各子工程及其相互制约的关系，其中以顶点表示活动，弧表示活动之间的优先制约关系，称这种有向图为顶点表示活动的网，简称AOV (Activity On Vertex network)网。

AOV 网的特点：

1.若从 i 到 j 有一条有向路径，则 i是 j 的前驱；j 是 i 的后继。

2.若 < i , j > 是网中有向边，则 i 是  j 的直接前驱； j 是 i 的直接后继。

3.AOV 网中不允许有回路，因为如果有回路存在，则表明某项活动以自己为先决条件，显然这是荒谬的。

 

2.拓扑排序:

在 AOV 网没有回路的前提下，我们将全部活动排列成一个线性序列，使得若 AOV 网中有弧 <i,  j> 存在，则在这个序列中， i  一定排在  j 的前面，具有这种性质的线性序列称为拓扑有序序列，相应的拓扑有序排序的算法称为拓扑排序。

拓扑排序的方法：

在有向图中选一个没有前驱的顶点且输出之。

从图中删除该顶点和所有以它为尾的弧。

重复上述两步，直至全部顶点均已输出；或者当图中不存在无前驱的顶点为止。

拓扑序列：

 

关键路径— 路径长度最长的路径

路径长度 — 路径上各活动持续时间之和。

把工程计划表示为有向图，用顶点表示事件，弧表示活动，弧的权表示活动持续时间。每个事件表示在它之前的活动已经完成，在它之后的活动可以开始。称这种有向图为边表示活动的网，简称为 AOE (Activity On Edge) 网

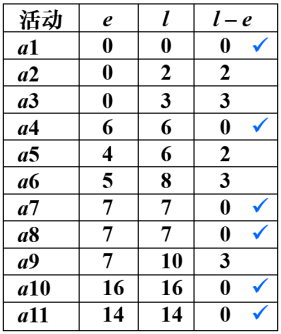
求关键路径步骤：   

求 ve(i)、vl(j)

求 e(i)、l(i)

计算 l(i) - e(i)

 

 

最短路径（在有向网中 A 点（源点）到达 B 点（终点）的多条路径中，寻找一条各边权值之和最小的路径，即最短路径）

最短路径与最小生成树不同，路径上不一定包含 n 个顶点，也不一定包含 n - 1 条边。

两种最常见的最短路径问题：

单源点最短路径（从某个源点到其余各顶点的最短路径 ）、所有顶点间的最短路径（每对顶点间的最短路径）