转置卷积（反卷积）为什么姓转置

转置卷积（反卷积）--为什么姓 转置

我们都知道常规的卷积操作：通过卷积将一个 高维度的特征，转移（仿射）到一个低维度。如下图

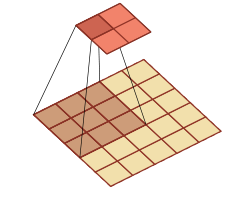
一个5 X5 的特征，通过一个3X3的卷积，步长=2，没有填充，一顿操作之后就可以将5X5 ----->2X2。这就是常规的卷积操作。

从数学的仿射角度解释：

一个高纬度的向量 Z （假设维度=5），和一个低维度向量X（假设维度=2），如果要用一个仿射变换来实现，就是利用矩阵W（因为矩阵的作用就是做一个空间变换嘛）操作，那么这个矩阵的维度应该等于 2X5。

所以用公式表示就是：

                                                                        

通过这样的一个仿射变换 就可以把一个5维向量，转移到一个2维的空间里。这就是常规的卷积操作。

如果要从现在的低维度变换到之前的高纬度，应该怎么搞？当然还是用矩阵啦

公式表示如下：

                                                                         

W转置之后就是一个5X2的矩阵，X是2维的 ，一顿操作就得到一个5维的向量了。

因此在卷积操作中，从低维度到高纬度的操作，叫做转置卷积（也叫反卷积）。

转置卷积效果图：https://nndl.github.io/v/cnn-conv-more

 

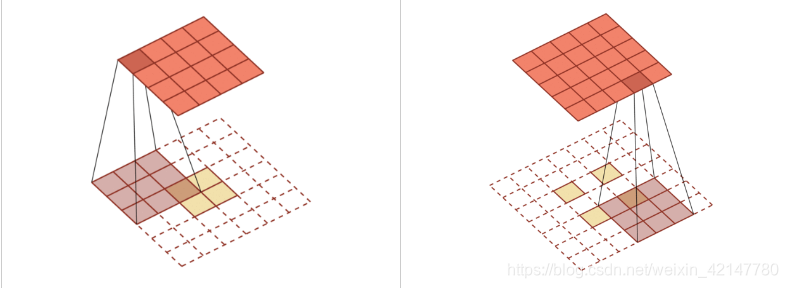
左边的图的实现方式就是通过在周低维特征图两边填充，然后再实施常规的卷积运算，就可以实现转置的效果。

右边的图的实现方式就是通过在 特征图中插入空格--微步卷积。

转置卷积在图像分割中应用很多。

下采样--就是常规的卷积，一张大图像经过多层卷积之后变成了低维度的特征图。

上采样-利用反卷积可以实现，一个低维度到高纬度的华丽转变。

 

——————待丰富——————

 

 

参考资料：

《神经网络语深度学习》--邱锡鹏--第5章