Gradient Descent 李宏●机器学习

● Loss function最小的一组参数

●计算偏微分，update参数。

●virtualize parameters

• 红色的箭头:梯度，是一个向量，也是等高线的法线方向.

• 蓝色的梯度：update参数，就梯度*lr，取一个负号，在加上theta0得到theta1.

• 步骤就反复地进行下去，再计算一遍梯度，得到另外一个红色的箭头，走的方向是红色箭头相反的方向。一直进行下去。算一次Gredient，决定要走的方向.
  
  ●Tip 1
  

• 关于learning rate 大小

  • 太小：走的太慢.
  • 太大：会震荡，永远走不下去。甚至一瞬间飞出去，loss function反而越来越大.
    

●visualize参数变化对应的loss function.

• 蓝色太小:下降非常非常的慢.
• 绿色太大：loss先快速的下降，接下来卡住了.
• 橘色过于太大：loss 直接飞出去！
• 红色刚刚好：得到一个好结果.

●Adagrad

刚开始离目标比较远，lr比较大，快点到最低点，接近目标后，减小lr，让它收敛在最低的地方.
可这样设learning rate :

这样是不够的，最好的状况是每个不同的参数都匹配一个learning rate
有很多小技巧，最容易简单的------Adagrad

Adagrad:每一个参数的learning rate都把它除以之前算出来的微分值的root mean square(均方根).
我们原来的gradient descent是这样：

其中

假设W呢，是某一个参数。现在的w不是一组参数，而是我们只考虑一个参数。因为我们现在在做Adagrad，adagrad的每一个参数都有不同的learning rate,所以呢，我们要把每一个参数都分开来考虑。w是一个参数，w的learning rate，在一般的gradient descent中，可能就给他一个depend on 时间的值，比如说 。但是，你可以把这件事情做得更好：

在adagrad里面呢，你把除以过去所有的微分的值的均方根。这个值对每一个参数而言，都是不一样。所以现在变成说，不同的参数，他的learning rate都是不一样的。
我们来实际举一个例子，来看这件事情是怎么做的。
假设初始的值是w0,接下来计算w0点的微分g0。他的learning rate是什么呢，是。是一个时间depend的参数，过去所有微值的均方根。在这里，之前算过一个，所以是根号g0的平方。以此类推。

所以呢，我们用adagrad的时候呢。他update的式子呢，可以写成下图中上式子。但是发现，分子分母都可以约掉根号t+1。所以式子可以化简。

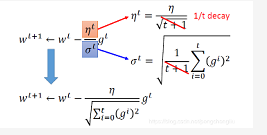
这个方法你可以接受么？大家有问题么？
Adagrad他的参数uptate其实是越来越慢的。如果不喜欢这个结果的话，有很多比这个更强的方法。Adaptive learning rate其实是一些列的方法，今天将的adagrad其实是里面最简单的。有很多其他的，差不多都是用“ada-”开头这样。所以，如果你用别的方法，比如adam,它就比较不会有这样的情形。如果，其实你没有什么特别的偏好的话，其实你可以用adam,他现在应该是我觉得最稳定的。但是他的实现比较复杂，但是其实也没有特别复杂

大家还有什么问题么？

好，我其实是有一个问题。我们在做一般的gradient descent的时候，我们参数的update取决于两件事情，一件事情是learning rate，另外一件事情是gradient。我们一直说，gradient越大，参数update的就越快。我相信你可以接受这件事情。但是在adagrad里面，你不觉得相当矛盾么，有些怪怪的地方。右边一项说，微分的值越大，参数update的越快。但是下面一项是相反的，当微分越大的时候，底下算出来的这一项越大，参数update的步伐越小。这不就跟我们原来要做的事情有所冲突的么？分子说gradient越大，参数update越大，分母说gradient越大，参数update的越小。好，怎么解释这件事情呢？

有一些paper是这样解释的。这个adagrad想要考虑的是，今天这个gradient有多surprise，也就是所谓的“反差”。反差大家都知道么。反差就是如果本来很凶恶的角色，突然对你很温柔这样子，就会觉得特别温柔。对gradient来说，也是一样的道理。假设有某一个参数，他在刚开始参数gradient为0.001，之后是0.001,0.003，。。到某一次呢，gradient算出来是0.1,你就觉得特别大。因为比之前的gradient算出来大了100倍。但是，如果有另外一个参数，他一开始算出来是10.8，然后是20.9,31.7,…但是，在某一次呢，他算出来是0.1，这时候就会觉得他特别小。所以为了强调这种反差的效果，所以在adagrad里面呢，我们就把它除以根号平方和这一项。这一项呢，就是把过去的gradient的平方和算出来，这样就知道过去gradient有多大，然后相除，看看反差有多大。

上面是直观的解释。更正式的解释呢，我有这样的解释：
我们来考虑一个二次函数，这个二次函数为，它只有一个参数x。求微分为2ax+b。最低点在-b/2a。高中就学过。

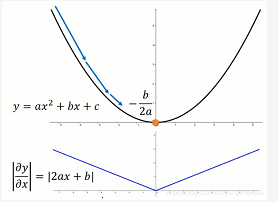
如果，今天呢，在这个二次函数上，随机地选一个点开始，要做gradient descent。那你的步伐踏出去多大是最好的呢？假设起始点是x0,最低点是-b/2a。那踏出去的一步最好的步伐其实就是这两个点之间的距离，因为如果踏出去的距离是这两个点之间的距离的话，就一步到位了。这两个点之间的距离就是x0+b/2a，整理一下就是(2ax0+b)/2a。

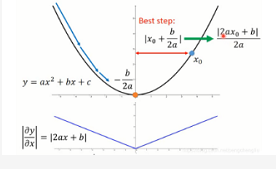
分子2ax0+b就是导数这一项。就是x0这一点的微分。所以，gradient descent 听起来很有道理，就是说，如果我今天算出来的微分越大，我就离最低点越远，如果我踏出去的最好的步伐是跟微分的大小成正比。

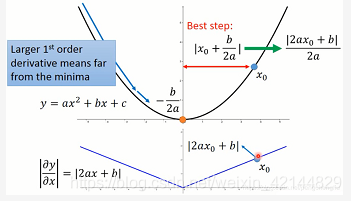
所以呢，如果踏出去的步伐跟微分成正比，他可能是最好的步伐。但是呢，这个事情是在只考虑一个参数的时候才成立。如果我们今天呢，我们要同时考虑好几个参数，这个时候呢，刚才的论述就不见得成立了。也就是说，gradient的值越大，就跟最低点的距离越远，这一件事情，在有好多个参数的时候，是不一定成立的。

比如，我们考虑w1和w2这两个参数。这个图上的颜色是他的loss.如果我们考虑w1的变化，我们就在这个蓝色这条线切一刀。我没看到error的surface（表面）长这样。如果比较图上的a点和b点，确实a点的微分值比较大，它离最低点比较远。

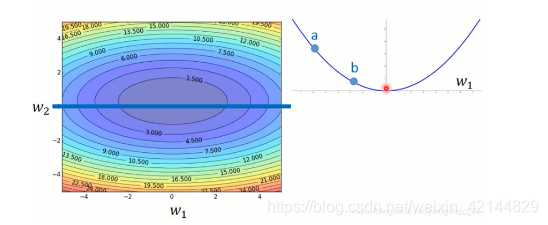
我们考虑w2这个参数，在绿色这条线上切一刀。我们得到的值是这样子。得到的error surface是这样。它是比较尖的，谷是比较深的。w2在这个方向的变化是比较猛烈的。如果我们只比较这根线上的两个点c跟d的话，确实c的微分比较大，距离最低点比较远。

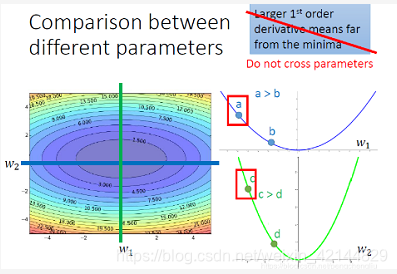
但是如果今天比较跨参数的话，如果我们比较a点和c点，我们比较a这个点对w1的微分和c这个点对w2的微分。这个结论呢，就不成立了。虽然说c这个点的微分值是比较大的，a点的微分值是比较小的，但是c离最低点是比较近的，a离最低点是比较远的。所以，更新参数跟微分的值成正比，这样的论述是在没有考虑跨参数的情境下才成立的。当我们同时考虑好几个参数的时候，我们这样想呢，就不足够了。

所以我们今天要同时考虑好几个参数的时候，我们要怎么想呢？我们看刚才的最好的步伐，除了分子之外，分母还有2a,这个2a是什么呢？如果把y做二次微分，就会得到2a。所以今天最好的step他不只是要正比于一次微分，他同时要和二次微分的大小成反比。

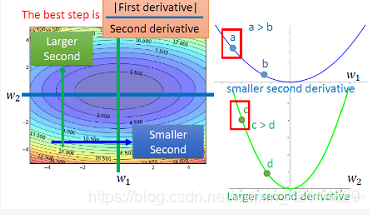
好，这件事情，跟adagrad的关系是什么呢？

如果你把adagrad的式子列出来的话，参数的update的量是左边这个样子。是一个常量，所以不理他。就是一次微分。下面这个所有过去微分值的平方和再开根号，它想要代表的就是二次微分。你可能会说，怎么不直接算二次微分呢？确实可以做二次微分，但是有时候你会遇到的状况是，参数量大，data多，可能算二次微分要花很长的时间。有时候这样的结果是你不能承受的。而且多花时间不一定效果好。adagrad的做法就是，我们在没有增加任何额外运算的前提之下，想办法能不能做一件事情去估一下二次微分是多少。在adagrad里面，只需要一次微分的值，而这个本来就是要算的，所以没有多做多余的任何运算。

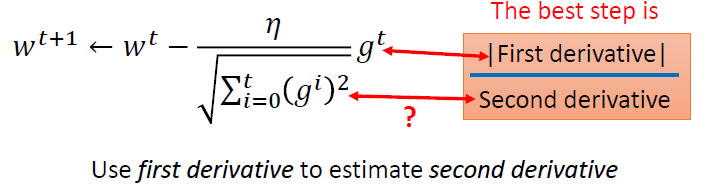
那怎么做呢？如果我们考虑一个二次微分比较小的峡谷跟一个二次微分比较大的峡谷。他们的一次微分为下面的图。
如果只是随机sample一个点，算他的一次微分的话，你看不出来他的二次微分的值是多少。

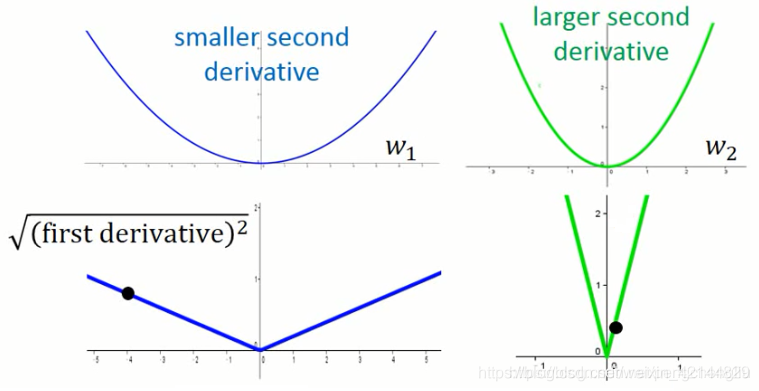
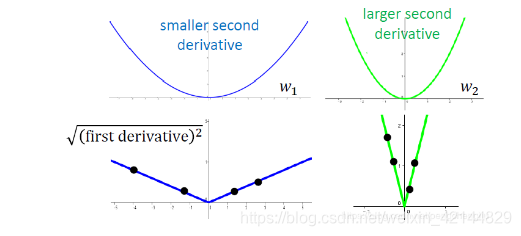
但是，如果你sample够多点，你就会发现说，在比较平滑的峡谷里面，他的一次微分通常是比较小的；在比较尖的峡谷里面，他的微分通常是比较大的。而adagrad中过去微分值的平方和再开根号，就相当于sample的这些点做平方和再开根号，就反映了二次微分的大小。adagrad怎么做，我们上次有示范过，就不在示范了。

接下来，我们要讲的另外一件事情呢，是stochastic gradient descent （随机梯度下降）。他可以让你的training 更快一点。

●Stochastic Gradient Descent（随机梯度下降法）

这个怎么说呢，我们之前的Regression里面讲，Loss function 长这样：

这个式子非常合理，我们本来就应该考虑所有的sample。有了这些以后，就可以做gradient descent。但是stochastic gradient descent 它的想法就不一样，它每次就拿一个example xn出来（你可以按照顺序去，也可以随机取。），然后计算Loss，Loss呢，只考虑一个example。不做summation了。我们写作L上标n，表示考虑第n个example的Loss function。接下来呢，在update参数的时候，你只算L上标n的gradient。然后就很急躁的update参数了。所以在原来的gradient descent里面，要计算所有data的loss，然后再update参数。但是在随机梯度下降法里面，你看一个example就更新一下参数。这有啥好呢？听起来好像没有什么好的。

那我们来实际操作一下。

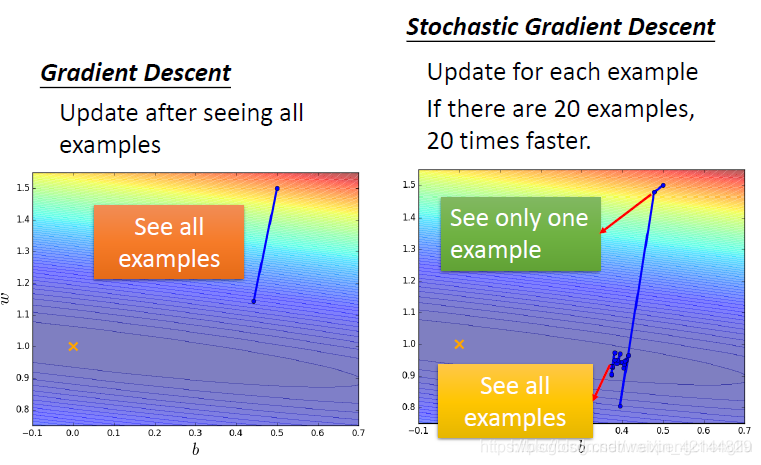
我们看到的图呢，可能是这样。原来的gradient descent，看完一遍example之后，就更新一遍参数。你会发现他是比较稳定的，他走的方向就是按照gradient descent 建议我们的方向来走。但是如果你是随机梯度下降的话，你每看一个example，你就update一次参数，如果你有20个example的时候，那你就update20次参数。所以当左边update一次的时候，右边已经update20次参数。右边，如果只看一个参数的话，他的步伐是小的，而且可能是散乱的，因为你每次只考虑一个example，他update的方向跟gradient descent 的tool Loss的error surface建议我们的方向不见得是一致的，但是因为我们可以看很多个example，左边走一步的时候，右边已经走了20步了，所以他走得反而是比较快的。

所谓的feature scaling的意思呢，是这样。假设现在我们要做Regression，那我们这个Regression 的function中input的feature有两个x1和x2。如果x1和x2他们的分布的range很不一样的话，那就建议你把他们做scaling。把他们range的分布变成是一样的。举例来说，x2他的分布呢，是远比x1大的。那就建议你呢，把x2做一下scaling，把他的值呢缩小，让x2的分布跟x1的分布是比较像的。希望不同的feature他们的scaling是一样的。

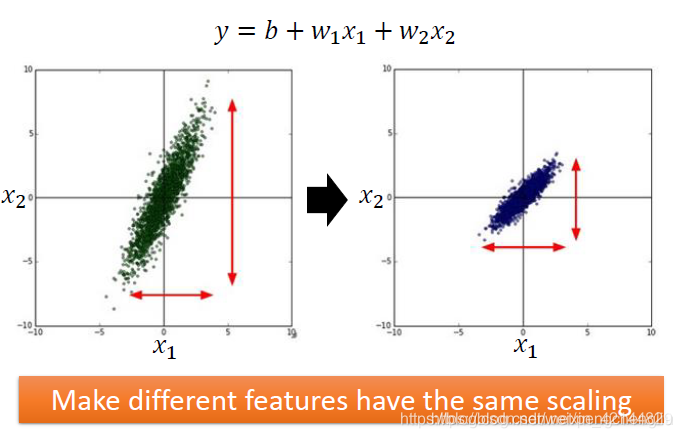
为什么要这么做呢？我们举一个例子。假设下面是我们的Regression的function。写成这样跟意思是一样的。

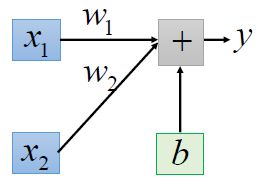
假设x1平常的值都是比较小的，比如说1啊,2啊之类的。假设x2平常的值都很大，都是100啊，200啊之类的 。那把Loss的surface画出来，会遇到什么状况呢?你会发现，如果你更改w1和w2的值，假设你把w1和w2的值都做一样的变动，都加个daita w，你会发现w1的变化对y的变化是比较小的。w2的变化对y的变化而言是比较大的。这个是很合理的，因为你要把w2乘上100,200这些值，而w1乘上1,2这些值。如果w2乘上的这些值是比较大的，w2只需要做小小的变化，y就变化很大。所以把Loss的surface画出来，可能是下面这个样子：

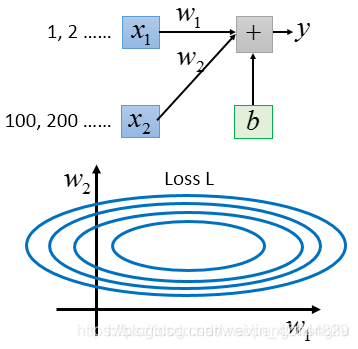
这个图呢，是什么意思呢？因为w1的变化的y的影响比较小，所以w1就对Loss的影响比较小。所以w1对Loss是有比较小的微分的。所以在w1这个方向上是比较平滑的。w2对y的影响比较大，所以对Loss的影响比较大。改变w2的时候对loss的影响比较大，所以在w2的方向上是比较sharp的，在w2这个方向上有一个比较尖的峡谷。
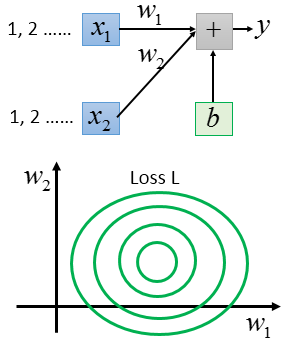
如果x1和x2他们的scale是接近的。如果你把Loss画出来的话呢，他就会比较接近圆形，因为w1和w2呢，对Loss是有差不多的影响力的。

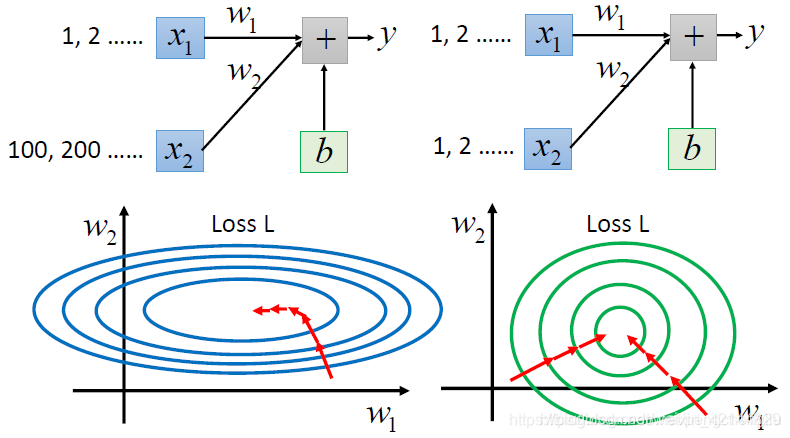
那这个对做gradient descent 会有什么样的影响呢？是会有影响的。比如从某个点开始，这种长椭圆的error surface，如果你不出些adagrad之类的方法，很难搞定它。因为在不同的方向上你会需要不同的learning rate，同一组learning rate你会搞不定他，一定要各自的learning rate才能搞定。所以没有scaling的时候，它update参数是比较难的。但是，如果你有scaling的话，他就变成正圆形。正圆形的时候，update参数就会变得比较容易。而且，你知道gradient descent并不是向着最低点走的，update的时候是顺着等高线的方向，是顺着gradient建议我们的方向。左边的图，虽然最低点在中间，但是不会指向最低点去走。但是右边的图呢，就不一样，如果是正圆的话，不管在区域的哪一个点，他都会向着圆心走。所以，如果有做scaling，在update参数的时候，是会比较有效率。

那怎么做scaling？方法有千百种。选一个你喜欢的就是了。常见的做法是这样的。假设我有R笔example，x1到xR。每一笔example里面都有一组feature。
那怎么做feature scaling，你就对每一个dimension i，都去算他的mean,写成mi；都去算他的stand deviation，写成。
然后对每一个example，比如第r个example的第i个component，减掉mi,再除以。做完这件事以后，所有dimension的mean就是0，variance就会是1。

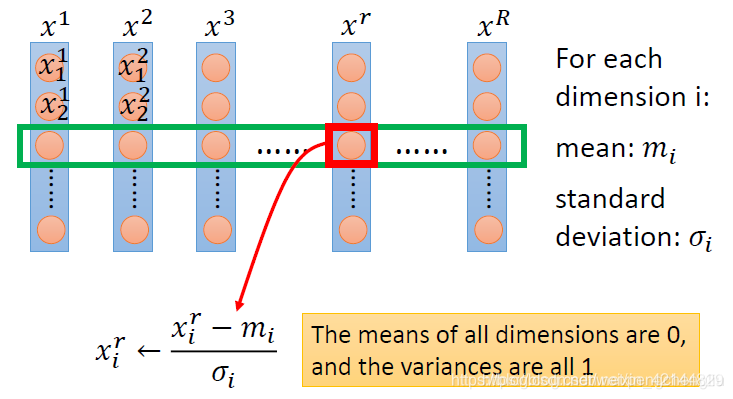
这就是常见的做normalization的方法。

最后，我们来讲一下为什么gradient descent他会work。他背后的理论基础是什么。