本文深入探讨深度学习中的优化算法，包括梯度下降法的各种形式：批量梯度下降法、随机梯度下降法和小批量梯度下降法，以及动量优化法如Momentum和NAG。此外，还介绍了自适应学习率优化算法如AdaGrad、Adadelta、RMSprop和Adam，并分析了各算法的表现。
文章目录
在花书深度学习第8章 Optimization for Training Deep Models中对机器学习中的优化器有如下定义:
finding the parameters θ \theta θ of a neural network that significantly reduce a cost function J ( θ ) J\left(\theta\right) J(θ), which typically includes a performance measure evaluated on the entire training set as well as additional regularization terms
梯度下降法(Gradient Descent)
在微积分中，对多元函数的参数求
δ
\delta
δ 偏导数，把求得的各个参数的导数以向量的形式写出来就是梯度。梯度就是函数变化最快的地方。梯度下降是迭代法的一种，在求解机器学习算法的模型参数
θ
\theta
θ 时，即无约束问题时，梯度下降是最常采用的方法之一。顾名思义，梯度下降法的计算过程就是沿梯度下降的方向求解极小值，也可以沿梯度上升方向求解最大值。
假设模型参数为
θ
\theta
θ ，损失函数为
J
(
θ
)
J\left(\theta\right)
J(θ)，损失函数
J
(
θ
)
J\left(\theta\right)
J(θ)关于参数
θ
\theta
θ的偏导数，也就是梯度为
▽
θ
J
(
θ
)
\triangledown _{\theta}J\left ( \theta \right )
▽θJ(θ)，学习率为
α
\alpha
α，则使用梯度下降法更新参数为：
θ
t
+
1
=
θ
t
−
α
⋅
▽
θ
J
(
θ
)
\theta_{t+1} = \theta_{t} -\alpha \cdot \triangledown _{\theta}J\left ( \theta \right )
θt+1=θt−α⋅▽θJ(θ)
梯度下降法目前主要分为三种方法,区别在于每次参数更新时计算的样本数据量不同：批量梯度下降法(BGD, Batch Gradient Descent)，随机梯度下降法(SGD, Stochastic Gradient Descent)及小批量梯度下降法(Mini-batch Gradient Descent)。
批量梯度下降法BGD
假设训练样本总数为n，样本为
{
(
x
1
,
y
1
)
,
⋯
,
(
x
n
,
y
n
)
}
\left \{ \left ( x^{1},y^{1} \right ) , \cdots, \left ( x^{n}, y^{n} \right )\right \}
{(x1,y1),⋯,(xn,yn)}，模型参数为
θ
\theta
θ ，损失函数为
J
(
θ
)
J\left(\theta\right)
J(θ)，在第
i
i
i对样本
(
x
1
,
y
1
)
\left ( x^{1},y^{1} \right )
(x1,y1)上损失函数关于参数的梯度为
▽
θ
J
i
(
θ
,
x
i
,
y
i
)
\triangledown_{\theta}J_{i}\left(\theta, x^{i}, y^{i} \right)
▽θJi(θ,xi,yi), 学习率为
α
\alpha
α，则使用BGD更新参数为：
θ
t
+
1
=
θ
t
−
α
t
⋅
∑
i
=
1
n
▽
θ
J
i
(
θ
,
x
i
,
y
i
)
\theta_{t+1} = \theta_{t} -\alpha_{t} \cdot \sum_{i=1}^{n} \triangledown_{\theta}J_{i}\left(\theta, x^{i}, y^{i} \right)
θt+1=θt−αt⋅i=1∑n▽θJi(θ,xi,yi)
由上式可以看出，每进行一次参数更新，需要计算整个数据样本集，因此导致批量梯度下降法的速度会比较慢，尤其是数据集非常大的情况下，收敛速度就会非常慢，但是由于每次的下降方向为总体平均梯度，它得到的会是一个全局最优解。
随机梯度下降法SGD
随机梯度下降法，不像BGD每一次参数更新，需要计算整个数据样本集的梯度，而是每次参数更新时，仅仅选取一个样本
(
x
i
,
y
i
)
\left ( x^{i},y^{i}\right )
(xi,yi)计算其梯度，参数更新公式为：
θ
t
+
1
=
θ
t
−
α
⋅
▽
θ
J
i
(
θ
,
x
i
,
y
i
)
\theta_{t+1} = \theta_{t} -\alpha \cdot \triangledown_{\theta}J_{i}\left(\theta, x^{i}, y^{i} \right)
θt+1=θt−α⋅▽θJi(θ,xi,yi)
可以看到BGD和SGD是两个极端，SGD由于每次参数更新仅仅需要计算一个样本的梯度，训练速度很快，即使在样本量很大的情况下，可能只需要其中一部分样本就能迭代到最优解，由于每次迭代并不是都向着整体最优化方向，导致梯度下降的波动非常大，更容易从一个局部最优跳到另一个局部最优，准确度下降。
小批量梯度下降法
小批量梯度下降法就是结合BGD和SGD的折中，对于含有n个训练样本的数据集，每次参数更新，选择一个大小为m
(
m
<
n
)
\left ( m < n \right )
(m<n)的mini-batch数据样本计算其梯度，其参数更新公式如下：
θ
t
+
1
=
θ
t
−
α
∑
i
=
x
i
=
x
+
m
−
1
⋅
▽
θ
J
i
(
θ
,
x
i
,
y
i
)
\theta_{t+1} = \theta_{t} -\alpha \sum_{i=x}^{i=x+m-1} \cdot \triangledown_{\theta}J_{i}\left(\theta, x^{i}, y^{i} \right)
θt+1=θt−αi=x∑i=x+m−1⋅▽θJi(θ,xi,yi)
小批量梯度下降法即保证了训练的速度，又能保证最后收敛的准确率，目前的SGD默认是小批量梯度下降算法。
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train_op = optimizer.minimize(loss, global_step=global_step)
SGD缺点：
- 选择合适的learning rate比较困难 ，学习率太低会收敛缓慢，学习率过高会使收敛时的波动过大
- 所有参数都是用同样的learning rate
- SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点
动量优化法
动量优化方法引入物理学中的动量思想，加速梯度下降，有Momentum和Nesterov两种算法。当我们将一个小球从山上滚下来，没有阻力时，它的动量会越来越大，但是如果遇到了阻力，速度就会变小，动量优化法就是借鉴此思想，使得梯度方向在不变的维度上，参数更新变快，梯度有所改变时，更新参数变慢，这样就能够加快收敛并且减少动荡。
Momentum
momentum算法思想：参数更新时在一定程度上保留之前更新的方向，同时又利用当前batch的梯度微调最终的更新方向，简言之就是通过积累之前的动量来加速当前的梯度。假设
m
t
m_t
mt表示t时刻的动量，
μ
\mu
μ表示动量因子，通常取值
0.9
0.9
0.9或者近似值，在SGD的基础上增加动量，则参数更新公式如下：
m
t
+
1
=
μ
⋅
m
t
+
α
⋅
▽
θ
J
(
θ
)
θ
t
+
1
=
θ
t
−
m
t
+
1
m_{t+1}=\mu \cdot m_{t} + \alpha \cdot \triangledown_{\theta} J \left(\theta \right) \\ \theta_{t+1}=\theta_{t} - m_{t+1}
mt+1=μ⋅mt+α⋅▽θJ(θ)θt+1=θt−mt+1
在梯度方向改变时，momentum能够降低参数更新速度，从而减少震荡；在梯度方向相同时，momentum可以加速参数更新， 从而加速收敛。总而言之，momentum能够加速SGD收敛，抑制震荡。
NAG（Nesterov accelerated gradient）
momentum保留了上一时刻的梯度
▽
θ
J
(
θ
)
\triangledown_{\theta} J \left(\theta \right)
▽θJ(θ)，对其没有进行任何改变，NAG是momentum的改进，在梯度更新时做一个矫正，具体做法就是在当前的梯度
▽
θ
J
(
θ
)
\triangledown_{\theta} J \left(\theta \right)
▽θJ(θ)上添加上一时刻的动量
μ
⋅
m
t
\mu \cdot m_{t}
μ⋅mt，梯度改变为
▽
θ
J
(
θ
−
μ
⋅
m
t
)
\triangledown_{\theta} J \left(\theta - \mu \cdot m_{t}\right)
▽θJ(θ−μ⋅mt)。
m
t
+
1
=
μ
⋅
m
t
+
α
⋅
▽
θ
J
(
θ
−
μ
⋅
m
t
)
θ
t
+
1
=
θ
t
−
m
t
+
1
m_{t+1}=\mu \cdot m_{t} + \alpha \cdot \triangledown_{\theta} J \left(\theta - \mu \cdot m_{t} \right) \\ \theta_{t+1}=\theta_{t} - m_{t+1}
mt+1=μ⋅mt+α⋅▽θJ(θ−μ⋅mt)θt+1=θt−mt+1
加上nesterov项后，梯度在大的跳跃后，进行计算对当前梯度进行校正。
下图是momentum和nesterrov的对比表述图：
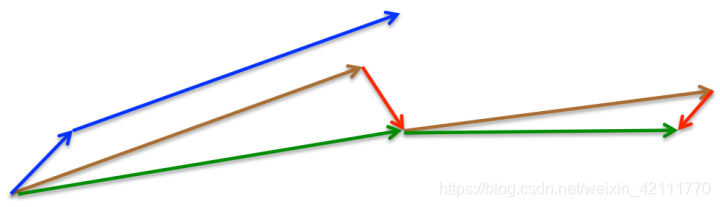momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)
自适应学习率优化算法
在机器学习中，学习率是一个非常重要的超参数，但是学习率是非常难确定的，虽然可以通过多次训练来确定合适的学习率，但是一般也不太确定多少次训练能够得到最优的学习率，玄学事件，对人为的经验要求比较高，所以是否存在一些策略自适应地调节学习率的大小，从而提高训练速度。
目前的自适应学习率优化算法主要有：AdaGrad算法，RMSProp算法，Adam算法以及AdaDelta算法。
AdaGrad
定义参数：全局学习率
δ
\delta
δ，一般会选择
δ
=
0.01
\delta=0.01
δ=0.01; 一个极小的常量
ϵ
\epsilon
ϵ ，通常取值
1
0
−
8
10^{-8}
10−8,目的是为了分母为0; 梯度加速变量(gradient accumulation variable)
r
r
r。
g
←
▽
θ
J
(
θ
)
r
←
r
+
g
2
△
θ
←
δ
r
+
ϵ
⋅
g
θ
←
θ
−
△
θ
g \leftarrow \triangledown_{\theta} J \left(\theta \right) \\ r \leftarrow r + g^{2} \\ \triangle \theta \leftarrow \frac{\delta }{\sqrt{r + \epsilon}}\cdot g\\ \theta \leftarrow \theta - \triangle \theta
g←▽θJ(θ)r←r+g2△θ←r+ϵδ⋅gθ←θ−△θ
从上式可以看出，梯度加速变量r为t时刻前梯度的平方和
r
=
∑
i
=
1
t
g
i
2
r = \sum_{i=1}^{t} g_{i}^{2}
r=∑i=1tgi2, 那么参数更新量
△
θ
\triangle \theta
△θ为
δ
⋅
1
∑
i
=
1
t
g
i
2
+
δ
⋅
g
\delta \cdot \frac{1}{\sqrt{\sum_{i=1}^{t}g_{i}^{2} + \delta}} \cdot g
δ⋅∑i=1tgi2+δ1⋅g，将
1
∑
i
=
1
t
g
i
2
+
δ
\frac{1}{\sqrt{\sum_{i=1}^{t}g_{i}^{2} + \delta}}
∑i=1tgi2+δ1看成一个约束项regularizer. 在前期，梯度累计平方和比较小，也就是r相对较小，则约束项较大，这样就能够放大梯度, 参数更新量变大; 随着迭代次数增多，梯度累计平方和也越来越大，即r也相对较大，则约束项变小，这样能够缩小梯度，参数更新量变小。
缺点：
仍需要手工设置一个全局学习率
δ
\delta
δ, 如果
δ
\delta
δ设置过大的话，会使regularizer过于敏感，对梯度的调节太大
中后期，分母上梯度累加的平方和会越来越大，使得参数更新量趋近于0，使得训练提前结束，无法学习
Adadelta
Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值
g
←
▽
θ
J
(
θ
)
n
t
←
v
⋅
n
t
−
1
+
(
1
−
v
)
⋅
g
t
2
θ
t
+
1
=
θ
t
−
δ
n
t
+
ϵ
⋅
g
t
g \leftarrow \triangledown_{\theta} J \left(\theta \right) \\ n_{t} \leftarrow v \cdot n_{t-1} + \left(1 -v \right) \cdot g_{t}^{2} \\ \theta_{t+1} = \theta_{t} - \frac{\delta}{\sqrt{n_{t} + \epsilon}} \cdot g_{t}
g←▽θJ(θ)nt←v⋅nt−1+(1−v)⋅gt2θt+1=θt−nt+ϵδ⋅gt
从上式中可以看出，Adadelta其实还是依赖于全局学习率
δ
\delta
δ，但是作者做了一定处理，经过近似牛顿迭代法之后
E
[
g
2
]
t
←
ρ
⋅
E
[
g
2
]
t
−
1
+
(
1
−
ρ
)
⋅
g
t
2
△
θ
←
∑
i
=
1
t
−
1
△
θ
r
E
[
g
2
]
t
+
ϵ
E \left[ g^{2}\right]_{t} \leftarrow \rho \cdot E \left[ g^{2}\right]_{t-1}+ \left(1 - \rho \right) \cdot g_{t}^{2} \\ \triangle \theta \leftarrow \frac{\sum_{i=1}^{t-1} \triangle \theta_{r}}{\sqrt{E \left[ g^{2}\right]_{t} + \epsilon}}
E[g2]t←ρ⋅E[g2]t−1+(1−ρ)⋅gt2△θ←E[g2]t+ϵ∑i=1t−1△θr
此时可以看出Adadelta已经不依赖全局learning rate了。
特点：
- 训练初中期，加速效果不错，很快。
- 训练后期，反复在局部最小值附近抖动。
RMSprop
RMSProp算法修改了AdaGrad的梯度平方和累加为指数加权的移动平均，使得其在非凸设定下效果更好。设定参数：全局初始率
δ
\delta
δ, 默认设为0.001; decay rate
ρ
\rho
ρ,默认设置为0.9,一个极小的常量
ϵ
\epsilon
ϵ ，通常为
1
0
−
6
10^{-6}
10−6
g
←
▽
θ
J
(
θ
)
E
[
g
2
]
t
←
ρ
⋅
E
[
g
2
]
t
−
1
+
(
1
−
ρ
)
⋅
g
t
2
△
θ
←
δ
E
[
g
2
]
t
+
ϵ
⋅
g
θ
←
θ
+
△
θ
g \leftarrow \triangledown_{\theta} J \left(\theta \right) \\ E \left[ g^{2}\right]_{t} \leftarrow \rho \cdot E \left[ g^{2}\right]_{t-1}+ \left(1 - \rho \right) \cdot g_{t}^{2} \\ \triangle \theta \leftarrow \frac{\delta }{\sqrt{E \left[ g^{2}\right]_{t} + \epsilon}}\cdot g\\ \theta \leftarrow \theta + \triangle \theta
g←▽θJ(θ)E[g2]t←ρ⋅E[g2]t−1+(1−ρ)⋅gt2△θ←E[g2]t+ϵδ⋅gθ←θ+△θ
特点：
- 其实RMSprop依然依赖于全局学习率 δ \delta δ
- RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
- 适合处理非平稳目标——对于RNN效果很好
Adam: Adaptive Moment Estimation
Adam中动量直接并入了梯度一阶矩（指数加权）的估计。其次，相比于缺少修正因子导致二阶矩估计可能在训练初期具有很高偏置的RMSProp，Adam包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩估计。
默认参数值设定为：
β
1
=
0.9
\beta_{1} = 0.9
β1=0.9,
β
2
=
0.999
\beta_{2} = 0.999
β2=0.999,
ϵ
=
1
0
−
8
\epsilon=10^{-8}
ϵ=10−8
g
←
▽
θ
J
(
θ
)
m
t
←
β
1
⋅
m
t
−
1
+
(
1
−
β
1
)
⋅
g
t
v
t
←
β
2
⋅
v
t
−
1
+
(
1
−
β
2
)
⋅
g
t
2
m
^
t
←
m
t
1
−
β
1
t
v
^
t
←
v
t
1
−
β
2
t
θ
t
+
1
=
θ
t
−
δ
ϵ
+
v
t
^
⋅
m
^
t
g \leftarrow \triangledown_{\theta} J \left(\theta \right) \\ m_{t} \leftarrow \beta_{1} \cdot m_{t-1} + \left(1 - \beta_{1} \right) \cdot g_{t} \\ v_{t} \leftarrow \beta_{2} \cdot v_{t-1} + \left( 1 - \beta_{2} \right) \cdot g_{t}^{2} \\ \hat{m}_{t} \leftarrow \frac{m_{t}}{1 - \beta_{1}^{t}} \\ \hat{v}_{t} \leftarrow \frac{v_{t}}{1 - \beta_{2}^{t}} \\ \theta_{t+1} = \theta_{t} - \frac{\delta}{\epsilon + \sqrt{\hat{v_{t}}}} \cdot \hat{m}_{t}
g←▽θJ(θ)mt←β1⋅mt−1+(1−β1)⋅gtvt←β2⋅vt−1+(1−β2)⋅gt2m^t←1−β1tmtv^t←1−β2tvtθt+1=θt−ϵ+vt^δ⋅m^t
其中，
m
t
m_{t}
mt，
n
t
n_{t}
nt分别是对梯度的一阶矩估计和二阶矩估计；
m
^
t
\hat{m}_{t}
m^t，
n
^
t
\hat{n}_{t}
n^t是对
m
t
m_{t}
mt，
n
t
n_{t}
nt的偏差校正，这样可以近似为对期望的无偏估计
特点：
- Adam梯度经过偏置校正后，每一次迭代学习率都有一个固定范围，使得参数比较平稳。
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化问题——适用于大数据集和高维空间。
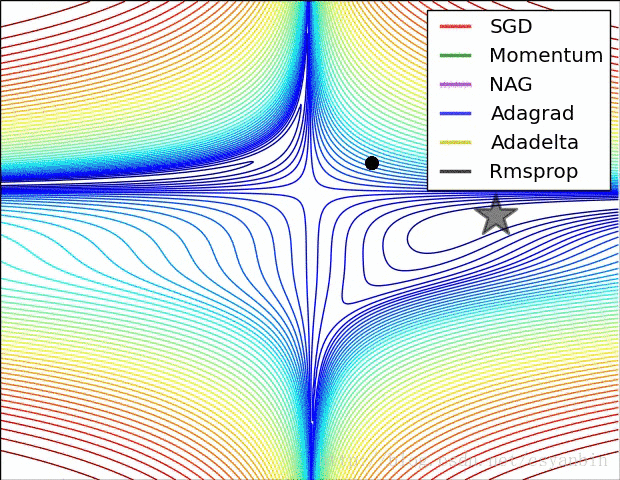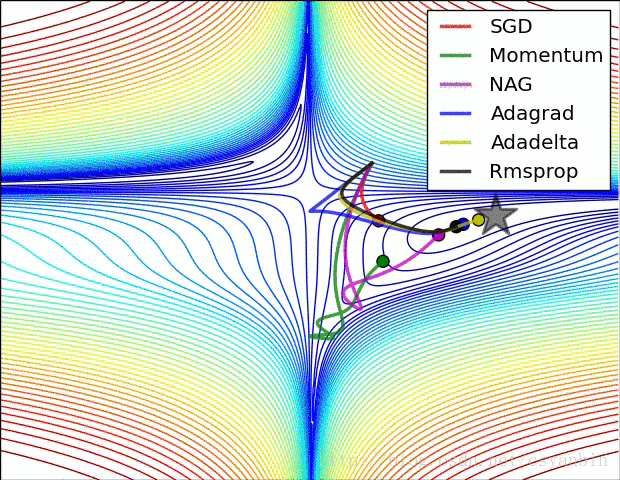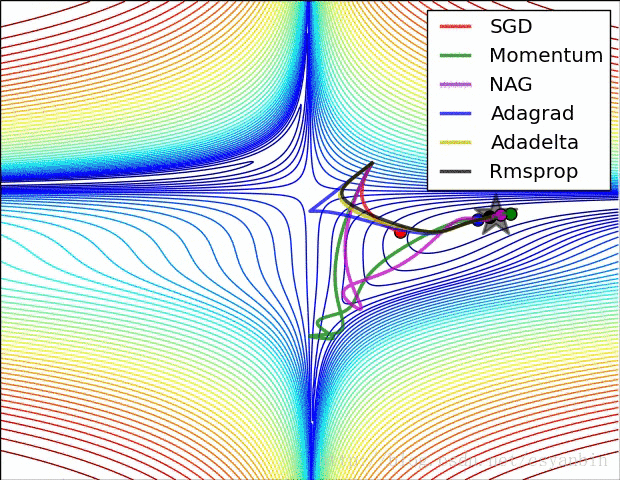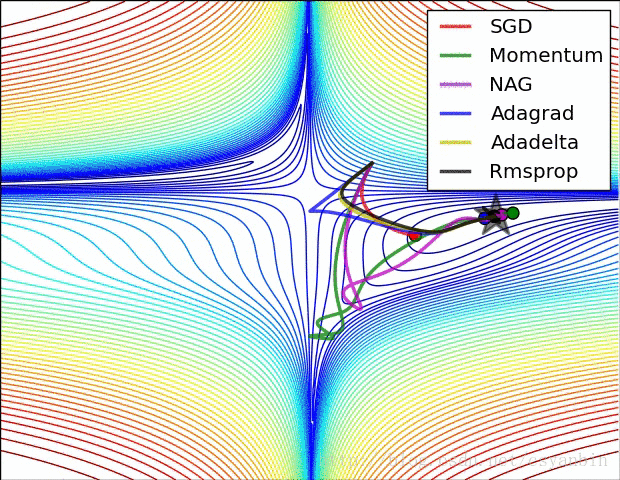
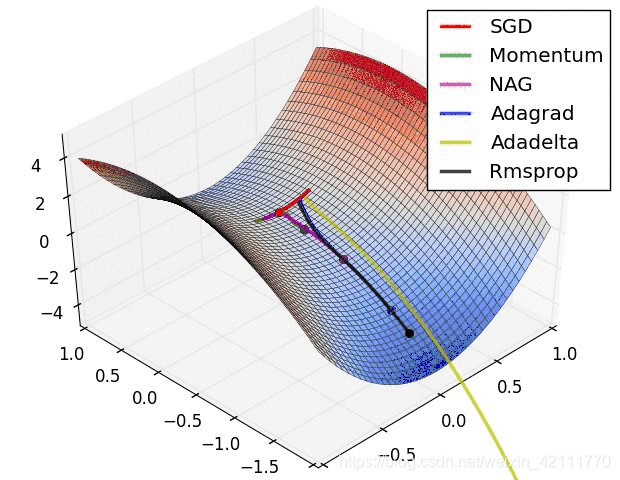
算法的表现
下图是各个算法在等高线的表现，它们都从相同的点出发，走不同的路线达到最小值点。可以看到，Adagrad，Adadelta和RMSprop在正确的方向上很快地转移方向，并且快速地收敛，然而Momentum和NAG先被领到一个偏远的地方，然后才确定正确的方向，NAG比momentum率先更正方向。SGD则是缓缓地朝着最小值点前进。
参考文献：
- An overview of gradient descent optimization algorithms
- 机器学习：各种优化器Optimizer的总结与比较机器学习：各种优化器Optimizer的总结与比较
- optimizer优化算法总结
- 深度学习最全优化方法总结比较(SGD，Adagrad，Adadelta，Adam，Adamax，Nadam)
- 自适应学习率的优化算法（from goodfellow deep learning)
- 深度学习—优化器算法Optimizer详解（BGD，SGD，MBGD，Momentum，NAG，Adagrad，Adadelta，RMSprop，Adam)
- tensorflow-Optimizer
扫一扫
14万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
