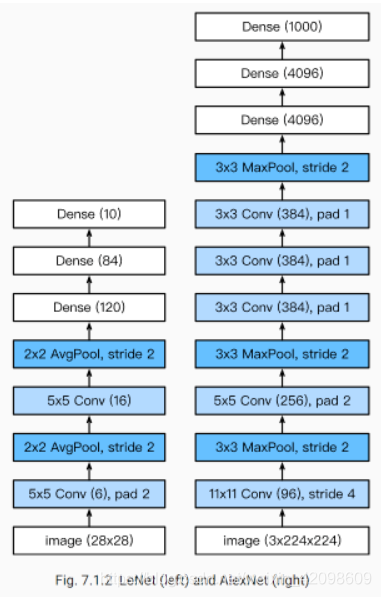
LeNet
用全连接层的局限性:
- 图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
- 对于大尺寸的输入图像,使用全连接层容易导致模型过大。
使用卷积层的优势:
- 卷积层保留输入形状。
- 卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算,从而避免参数尺寸过大。
LeNet结构
LeNet分为卷积层块和全连接层块两个部分。

网络模型与输入
#net
class Flatten(torch.nn.Module): #展平操作
def forward(self, x):
return x.view(x.shape[0], -1)
class Reshape(torch.nn.Module): #将图像大小重定型
def forward(self, x):
return x.view(-1,1,28,28) #(B x C x H x W)
net = torch.nn.Sequential( #Lelet
Reshape(),
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2), #b*1*28*28 =>b*6*28*28
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), #b*6*28*28 =>b*6*14*14
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5), #b*6*14*14 =>b*16*10*10
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), #b*16*10*10 => b*16*5*5
Flatten(), #b*16*5*5 => b*400
nn.Linear(in_features=16*5*5, out_features=120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10)
)
这里记一下evaluate_accuracy函数中net.eval()函数的用法
#计算准确率
'''
(1). net.train()
启用 BatchNormalization 和 Dropout,将BatchNormalization和Dropout置为True
(2). net.eval()
不启用 BatchNormalization 和 Dropout,将BatchNormalization和Dropout置为False
'''
def evaluate_accuracy(data_iter, net,device=torch.device('cpu')):
"""Evaluate accuracy of a model on the given data set."""
acc_sum,n = torch.tensor([0],dtype=torch.float32,device=device),0
for X,y in data_iter:
# If device is the GPU, copy the data to the GPU.
X,y = X.to(device),y.to(device)
net.eval()
with torch.no_grad():
y = y.long()
acc_sum += torch.sum((torch.argmax(net(X), dim=1) == y)) #[[0.2 ,0.4 ,0.5 ,0.6 ,0.8] ,[ 0.1,0.2 ,0.4 ,0.3 ,0.1]] => [ 4 , 2 ]
n += y.shape[0]
return acc_sum.item()/n
深度卷积神经网络(AlexNet)
机器学习的特征提取:手工定义的特征提取函数
神经网络的特征提取:通过学习得到数据的多级表征,并逐级表⽰越来越抽象的概念或模式。
AlexNet
首次证明了学习到的特征可以超越⼿⼯设计的特征,从而⼀举打破计算机视觉研究的前状。
特征:
- 8层变换,其中有5层卷积和2层全连接隐藏层,以及1个全连接输出层。
- 将sigmoid激活函数改成了更加简单的ReLU激活函数。
- 用Dropout来控制全连接层的模型复杂度。
- 引入数据增强,如翻转、裁剪和颜色变化,从而进一步扩大数据集来缓解过拟合。
网络中的网络(NiN)
LeNet、AlexNet和VGG:先以由卷积层构成的模块充分抽取 空间特征,再以由全连接层构成的模块来输出分类结果。
NiN:串联多个由卷积层和“全连接”层构成的小⽹络来构建⼀个深层⽹络。这里的“全连接”层其实是指1x1的卷积层,因为全连接层的输出维度无法作为下一个block的输入。
⽤了输出通道数等于标签类别数的NiN块,然后使⽤全局平均池化层对每个通道中所有元素求平均并直接⽤于分类。

1×1卷积核作用
1.放缩通道数:通过控制卷积核的数量达到通道数的放缩。
2.增加非线性。1×1卷积核的卷积过程相当于全连接层的计算过程,并且还加入了非线性激活函数,从而可以增加网络的非线性。
3.计算参数少
GoogLeNet
- 由Inception基础块组成。
- Inception块相当于⼀个有4条线路的⼦⽹络。它通过不同窗口形状的卷积层和最⼤池化层来并⾏抽取信息,并使⽤1×1卷积层减少通道数从而降低模型复杂度。
可以⾃定义的超参数是每个层的输出通道数,我们以此来控制模型复杂度。

完整结构图:

循环神经网络进阶
GRU
RNN存在的问题:梯度较容易出现衰减或爆炸(BPTT)
⻔控循环神经⽹络:捕捉时间序列中时间步距离较⼤的依赖关系
GRU:

R
t
=
σ
(
X
t
W
x
r
+
H
t
−
1
W
h
r
+
b
r
)
Z
t
=
σ
(
X
t
W
x
z
+
H
t
−
1
W
h
z
+
b
z
)
H
~
t
=
t
a
n
h
(
X
t
W
x
h
+
(
R
t
⊙
H
t
−
1
)
W
h
h
+
b
h
)
H
t
=
Z
t
⊙
H
t
−
1
+
(
1
−
Z
t
)
⊙
H
~
t
R_{t} = σ(X_tW_{xr} + H_{t−1}W_{hr} + b_r)\\ Z_{t} = σ(X_tW_{xz} + H_{t−1}W_{hz} + b_z)\\ \widetilde{H}_t = tanh(X_tW_{xh} + (R_t ⊙H_{t−1})W_{hh} + b_h)\\ H_t = Z_t⊙H_{t−1} + (1−Z_t)⊙\widetilde{H}_t
Rt=σ(XtWxr+Ht−1Whr+br)Zt=σ(XtWxz+Ht−1Whz+bz)H
t=tanh(XtWxh+(Rt⊙Ht−1)Whh+bh)Ht=Zt⊙Ht−1+(1−Zt)⊙H
t
• 重置⻔有助于捕捉时间序列里短期的依赖关系;
• 更新⻔有助于捕捉时间序列里长期的依赖关系。
长短期记忆(long short-term memory )
遗忘门:控制上一时间步的记忆细胞 输入门:控制当前时间步的输入
输出门:控制从记忆细胞到隐藏状态
记忆细胞:⼀种特殊的隐藏状态的信息的流动

I
t
=
σ
(
X
t
W
x
i
+
H
t
−
1
W
h
i
+
b
i
)
F
t
=
σ
(
X
t
W
x
f
+
H
t
−
1
W
h
f
+
b
f
)
O
t
=
σ
(
X
t
W
x
o
+
H
t
−
1
W
h
o
+
b
o
)
C
~
t
=
t
a
n
h
(
X
t
W
x
c
+
H
t
−
1
W
h
c
+
b
c
)
C
t
=
F
t
⊙
C
t
−
1
+
I
t
⊙
C
~
t
H
t
=
O
t
⊙
t
a
n
h
(
C
t
)
I_t = σ(X_tW_{xi} + H_{t−1}W_{hi} + b_i) \\ F_t = σ(X_tW_{xf} + H_{t−1}W_{hf} + b_f)\\ O_t = σ(X_tW_{xo} + H_{t−1}W_{ho} + b_o)\\ \widetilde{C}_t = tanh(X_tW_{xc} + H_{t−1}W_{hc} + b_c)\\ C_t = F_t ⊙C_{t−1} + I_t ⊙\widetilde{C}_t\\ H_t = O_t⊙tanh(C_t)
It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxo+Ht−1Who+bo)C
t=tanh(XtWxc+Ht−1Whc+bc)Ct=Ft⊙Ct−1+It⊙C
tHt=Ot⊙tanh(Ct)
深度循环神经网络

H
t
(
1
)
=
ϕ
(
X
t
W
x
h
(
1
)
+
H
t
−
1
(
1
)
W
h
h
(
1
)
+
b
h
(
1
)
)
H
t
(
ℓ
)
=
ϕ
(
H
t
(
ℓ
−
1
)
W
x
h
(
ℓ
)
+
H
t
−
1
(
ℓ
)
W
h
h
(
ℓ
)
+
b
h
(
ℓ
)
)
O
t
=
H
t
(
L
)
W
h
q
+
b
q
\boldsymbol{H}_t^{(1)} = \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(1)} + \boldsymbol{H}_{t-1}^{(1)} \boldsymbol{W}_{hh}^{(1)} + \boldsymbol{b}_h^{(1)})\\ \boldsymbol{H}_t^{(\ell)} = \phi(\boldsymbol{H}_t^{(\ell-1)} \boldsymbol{W}_{xh}^{(\ell)} + \boldsymbol{H}_{t-1}^{(\ell)} \boldsymbol{W}_{hh}^{(\ell)} + \boldsymbol{b}_h^{(\ell)})\\ \boldsymbol{O}_t = \boldsymbol{H}_t^{(L)} \boldsymbol{W}_{hq} + \boldsymbol{b}_q
Ht(1)=ϕ(XtWxh(1)+Ht−1(1)Whh(1)+bh(1))Ht(ℓ)=ϕ(Ht(ℓ−1)Wxh(ℓ)+Ht−1(ℓ)Whh(ℓ)+bh(ℓ))Ot=Ht(L)Whq+bq
双向循环神经网络

H
→
t
=
ϕ
(
X
t
W
x
h
(
f
)
+
H
→
t
−
1
W
h
h
(
f
)
+
b
h
(
f
)
)
H
←
t
=
ϕ
(
X
t
W
x
h
(
b
)
+
H
←
t
+
1
W
h
h
(
b
)
+
b
h
(
b
)
)
H
t
=
(
H
→
t
,
H
←
t
)
O
t
=
H
t
W
h
q
+
b
q
\begin{aligned} \overrightarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}_{t-1} \boldsymbol{W}_{hh}^{(f)} + \boldsymbol{b}_h^{(f)})\\ \overleftarrow{\boldsymbol{H}}_t &= \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}_{t+1} \boldsymbol{W}_{hh}^{(b)} + \boldsymbol{b}_h^{(b)}) \end{aligned}\\ \boldsymbol{H}_t=(\overrightarrow{\boldsymbol{H}}_{t}, \overleftarrow{\boldsymbol{H}}_t)\\ \boldsymbol{O}_t = \boldsymbol{H}_t \boldsymbol{W}_{hq} + \boldsymbol{b}_q
HtHt=ϕ(XtWxh(f)+Ht−1Whh(f)+bh(f))=ϕ(XtWxh(b)+Ht+1Whh(b)+bh(b))Ht=(Ht,Ht)Ot=HtWhq+bq

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








