剑指offer刷题-数组中重复的元素

最新推荐文章于 2022-07-29 22:12:24 发布

weixin_42048754

最新推荐文章于 2022-07-29 22:12:24 发布

阅读量292

点赞数

分类专栏：剑指offer刷题

本文链接：https://blog.youkuaiyun.com/weixin_42048754/article/details/105922684

版权

剑指offer刷题专栏收录该内容

36 篇文章

订阅专栏

本文探讨了在限定范围内的数组中查找重复数字的多种算法，包括使用TreeMap、辅助数组和原地置换策略，对比了不同方法的时间和空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

题目解读

牛客上给出的代码，是需要三个输入参数，分别为：原数组，数组长度，和数组Duplication，这个数组用来存储原数组中重复的元素，即Duplication[0]存储第一个重复的2。
目前代码要求是，只要检测出第一个重复元素就返回true。

思路：
一、
我自己的思路是通过TreeMap键值对的形式，将0~n-1作为键，默认值初始为0。
遍历原数组，在TreeMap中找到对应的键，将其对应值加一。如此，当检测到该键的值已经为一时，说明该数字已经出现过一次，即该值就是所求的第一个重复的数字。
PS：目前对于TreeMap掌握并不熟练，尚未实现。

二、
第二个思路是，创建另外一个与原数组等长度的新数组，新数组的下标为0~n-1。
遍历原数组，对每一个数字，在新数组的对应下标位置加一。如此，当发现新数组对应下标上的元素为1时，说明该数字已经出现过，则为重复数字。
PS：因为有新建数组，所以空间复杂度会较高。
代码实现：

public class Solution {
    public boolean duplicate(int numbers[],int length,int [] duplication) {
        int[] copynum = new int[length];
        if(numbers == null || length <= 0)
        {
            return false;
        }
        for(int temp:numbers)
        {
            while(copynum[temp] == 1)
            {
                
                duplication[0] = temp;
                return true;
            }
            copynum[temp]++;
        }
        return false;
    }
}

三、
牛客上的思路：
避免创建新数组造成额外空间的浪费，在原数组上进行元素交换。
从哈希表的思路拓展，重排数组：把扫描的每个数字（如数字m）放到其对应下标（m下标）的位置上，若同一位置有重复，则说明该数字重复。

时间复杂度为O(n),空间复杂度为O(1)；

遍历数组，判断当前位的值和下标是否相等：
1、若相等，则遍历下一位；
2、若不等，则将当前位置i上的元素和a[i]位置上的元素比较：若它们相等，则找到了第一个相同的元素；若不等，则将它们两交换。换完之后a[i]位置上的值 a[i] 和它的下标 a[i] 是对应的，但i位置上的元素和下标并不一定对应；重复2的操作，直到当前位置i的值也为i，将i向后移一位，再重复2。

public class Solution {    
	public boolean duplicate(int numbers[],int length,int [] duplication) {        
		if(numbers == null || numbers.length <= 0)        
		{            
			return false;        }        
		for( int number : numbers )        
			{            
			if(number < 0 || number >= length)            
			{                
				return false;            
			}        
		}                 
		for(int i = 0;i < length;i++)        {            
			while(numbers[i] != i)            {                
				if(numbers[numbers[i]] == numbers[i])
				//当检测到两个位置的元素相等时，说明有重复的元素Numbers[i]                
				{                    
					duplication[0] = numbers[i];                    
					return true;                
				}
				//交换numbers[i]和numbers[numbers[i]]位置的元素，使得numbers[numbers[i]]= numbers[i]              
				int temp = numbers[i];                
				numbers[i] = numbers[temp];                
				numbers[temp] = temp;                          			}        
		}        
		return false;     
	}
}

四、
网友的思路：（是错的）
不需要重排数组，减少交换次数。遍历数组，题目里写了数组里数字的范围保证在0 ~ n-1 之间，所以可以利用现有数组设置标志，当一个数字被访问过后，可以设置对应下标上的数 + n，之后再遇到相同的数时，会发现对应下标上的数已经大于等于n了，那么直接返回这个数即可，从而避免了元素交换。
代码出错：java.lang.ArrayIndexOutOfBoundsException: 6
超出索引？？？

懂啦

因为对于numbers[numbers[temp]] += length;中的numbers[temp]可能在其他元素下，已经加了length，造成此时作为索引的numbers[temp]已经超出了length数组长度，所以会报错，因此这种方法是不可行的。原因在于此时数组的元素不仅作为元素使用，也间接作为索引使用。

public class Solution {
   public boolean duplicate(int numbers[],int length,int [] duplication) {
        
        if(numbers == null || length <= 0)
        {
            return false;
        }
        for(int temp : numbers)
        {
            while(numbers[numbers[temp]] >= length)
            {
                duplication[0] = temp;
                return true;
            }
            numbers[numbers[temp]] += length;
        }
        return false;
    }
}

PS：补充关于TreeMap类的使用

TreeMap 类不仅实现了 Map 接口，还实现了 Map 接口的子接口 java.util.SortedMap。

TreeMap 类中不允许键对象为 null 或是基本数据类型，这是因为 TreeMap 中的对象必须是可排序的（即对象需要实现 java.lang.Comparable 接口）

在创建 TreeMap 对象时，如果使用参数为空的构造方法，则根据 Map 对象的 key 进行排序；如果使用参数为 Comparator 的构造方法，则根据 Comparator 进行排序。

HashMap VS. TreeMap

在添加、删除和定位映射关系上，TreeMap类要比HashMap类的性能差一些，但是TreeMap中的映射关系具有一定的顺序。

如果不需要一个有序的集合，则建议使用HashMap类；如果需要进行有序的遍历输出，则建议使用TreeMap类。在这种情况下，可以先使用 HashMap。在需要排序时，利用现有的 HashMap，创建一个 TreeMap 类型的实例。

HashMap的创建：Map<Number, Person> map = new HashMap<Number, Person>();
TreeMap的创建：TreeMap<Number, Person> treeMap = new TreeMap<Number, Person>();

红黑树

一、红黑树

TreeMap的实现是红黑树算法的实现，根据红黑树的算法来分析TreeMap的实现。

红黑树又称红-黑二叉树，它首先是一颗二叉树，它具体二叉树所有的特性。同时红黑树更是一颗自平衡的排序二叉树。

基本的二叉查找树需要满足一个基本性质–即树中的任何节点的值大于它的左子节点，且小于它的右子节点。按照这个基本性质使得树的检索效率大大提高。

红黑树顾名思义就是节点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。对于一棵有效的红黑树二叉树而言我们必须增加如下规则：
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点（NULL节点，空节点）是黑色的。
4、红节点的两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长路径不多于最短路径的两倍长。结果是这棵树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。所以红黑树它是复杂而高效的，其检索效率O(log n)。

对于红黑二叉树，主要有三个操作：左旋、右旋、上色。

二、TreeMap put()方法

1、红黑树增加节点
红黑树在新增节点过程中比较复杂，由于规则1、2、3基本都会满足，主要讨论规则4、5。有一棵最简单的树，新增的节点为N、它的父节点为P、P的兄弟节点为U、P的父节点为G。

在这里插入图片描述
对于新节点的插入：

1、插入新节点总是红色节点 。
2、如果插入节点的父节点是黑色, 能维持性质。
3、如果插入节点的父节点是红色, 破坏了性质. 故插入算法就是通过重新着色或旋转, 来维持性质。

情况一：为跟节点
若新插入的节点N没有父节点，则直接当做根据节点插入即可，同时将颜色设置为黑色。

情况二、父节点为黑色
新节点N直接插入，同时颜色为红色，根据规则4它会存在两个黑色的叶子节点，值为null。同时由于新增节点N为红色，所以通过它的子节点的路径依然会保存着相同的黑色节点数，同样满足规则5。
在这里插入图片描述
情况三、父节点P和P的兄弟节点U都为红色
对于这种情况若直接插入肯定会出现不平衡现象。怎么处理？P、U节点变黑、G节点变红。这时由于经过节点P、U的路径都必须经过G所以在这些路径上面的黑节点数目还是相同的。但是经过上面的处理，可能G节点的父节点也是红色，这个时候我们需要将G节点当做新增节点递归处理。
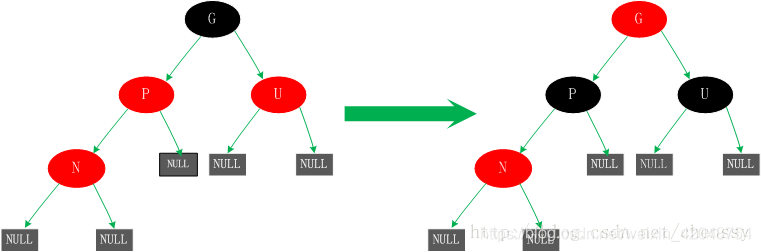
在这里插入图片描述
情况四、若父节点P为红色，叔父节点U为黑色或者缺少，且新增节点N为P节点的右孩子
对新增节点N、P进行一次左旋转。这里所产生的结果其实并没有完成，还不是平衡的（违反了规则四），这是我们需要进行情况5的操作。
在这里插入图片描述
情况五、父节点P为红色，叔父节点U为黑色或者缺少，新增节点N为父节点P左孩子

这种情况有可能是由于情况四而产生的，也有可能不是。对于这种情况：1、以P节点为中心进行右旋转，在旋转后产生的树中，节点P是节点N、G的父节点。但是这棵树并不规范，它违反了规则4；2、**将P、G节点的颜色进行交换，（并使U变黑？？**使之其满足规范。开始时所有的路径都需要经过G其他们的黑色节点数一样，但是现在所有的路径改为经过P，且P为整棵树的唯一黑色节点，所以调整后的树同样满足规范5。
在这里插入图片描述
后续在https://blog.youkuaiyun.com/chenssy/article/details/26668941中有详细解释，在此不展开