《机器学习实战》——支持向量机SVM

一、前言  

      这应该是我第一次写博客，写的不好，还请各位大神多多指教……

       学习机器学习已经有一段时间了，已经稍稍入了点门了，但是总感觉对数据的处理理解不到位，苏安然跟着书把代码实现了，但怎样实现的还是不清楚，希望继续学习下去，可以把这一点搞清楚吧。

二、基本概念

       下面进入正题，学习支持向量机，首先得理解支持向量机的基本概念。在线性可分（对于一个数据集合能否画一条直线将两组数据点分开）的数据中，将数据集分隔开来的直线成为分隔超平面。对于二维平面来说，分隔超平面就是一条直线，但对于三维及以上数据来说，该对象就是超平面，也就是分类的决策边界。如下图所示：

                                                     

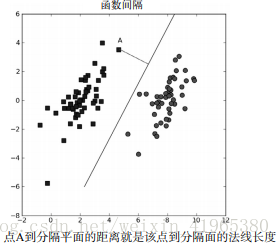
       我们希望采用一种方式来构建分类器，即如果数据点离决策边界越远，那么其最后的预测结果也就越可信，我们希望找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能远，这里点到分隔面的距离被称为间隔，支持向量（support vector）就是离分隔超平面最近的那些点。最大化支持向量到分隔面的距离，就需要找到优化求解方法来寻找最大间隔。

       支持向量是一种二类分类器。之所以称为“机”，是因为它会产生一个二值决策结果，即它是一种决策“机”。

三、SMO高效优化算法

       SMO表示序列最小优化，就是将大优化问题分解成多个小优化问题来求解，这些小优化问题往往很容易求解，并且对它们进行顺序求解的结果与将它们作为整体来求解的结果完全一致，但SMO算法的求解时间短很多。

       SMO算法的目标是求出一系列的alpha和b，一旦求出了这些alpha，就很容易计算出权重向量w并得到分隔超平面。

       SMO算法的工作原理：每次循环中选择两个alpha进行优化处理。一旦找到一对合适的alpha，那么就增大其中一个同事减小另一个。所谓“合适”是指两个alpha必须要符合一定的条件，条件之一是这两个alpha必须要在间隔边界之外，第二个条件则是这两个alpha还没有进行过区间化处理或者不在边界上。

1、简化版SMO算法处理小规模数据集

       

#loadDataSet()函数：打开文件并对其进行逐行解析
#从而得到每行的类标签和整个数据矩阵
def loadDataSet(fileName):
	dataMat = []; labelMat = []
	fr = open(fileName)
	for line in fr.readlines():
		lineArr = line.strip().split('\t')
		dataMat.append([float(lineArr[0]), float(lineArr[1])])
		labelMat.append(float(lineArr[2]))
	return dataMat,labelMat
#构建辅助函数1：在某个区间范围内随机选择一个整数，只要函数值不等于输入值i，函数就会进行随机选择。
#i是第一个alpha的下标，m是alpha的数目
def selectJrand(i,m):
	j = i
	while (j==i):
		j = int(random.uniform(0,m))
	return j
#构建辅助函数2：对于数值不在范围内时对其进行调整，调整大于H或小于L的alpha值。
def clipAlpha(aj,H,L):
	if aj > H:
		aj = H
	if L > aj:
		aj = L
	return aj

SMO函数的伪代码如下：

#创建一个alpha向量并将其初始化为0向量
#当迭代次数小于最大迭代次数时（外循环）
    #对数据集中的每个数据向量（内循环）：
        #如果该数据向量可以被优化：
            #随机选择另外一个数据向量
            #同时优化这两个向量
            #如果两个向量都不能被优化，退出内循环
    #如果所有向量都没有被优化，增加迭代数目，继续下一次循环

简化版SMO算法：

#dataMat    ：数据列表
#classLabels：标签列表
#C          ：权衡因子（增加松弛因子而在目标优化函数中引入了惩罚项）
#toler      ：容错率
#maxIter    ：最大迭代次数
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
	dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
	b = 0; m,n = shape(dataMatrix)
	alphas = mat(zeros((m,1)))
	iter = 0
	while (iter < maxIter):
		alphaPairsChanged = 0
		for i in range(m):
			fXi = float(multiply(alphas,labelMat).T*\
			(dataMatrix*dataMatrix[i,:].T)) + b
			Ei = fXi - float(labelMat[i])
			if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or \
			((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
				j = selectJrand(i,m)
				fXj = float(multiply(alphas,labelMat).T*\
					(dataMatrix*dataMatrix[j,:].T)) + b
				Ej = fXj - float(labelMat[j])
				alphaIold = alphas[i].copy();
				alphaJold = alphas[j].copy();
				if (labelMat[i] != labelMat[j]):
					L = max(0, alphas[j] - alphas[i])
					H = min(C, C + alphas[j] - alphas[i])
				else:
					L = max(0, alphas[j] + alphas[i