剑指Offer(牛客版)--面试题33：二叉树的后序遍历序列

最新推荐文章于 2022-05-12 15:25:23 发布

原创最新推荐文章于 2022-05-12 15:25:23 发布 · 284 阅读

0 ·

CC 4.0 BY-SA版权

剑指Offer(牛客版）专栏收录该内容

73 篇文章

订阅专栏

本文介绍了一个算法，用于判断一个整数数组是否为二叉搜索树的后序遍历结果。通过分析数组元素与根节点的关系，递归判断左右子树是否符合二叉搜索树的特性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true，否则返回false。假设输入的数组的任意两个数字都互不相同。

分析：

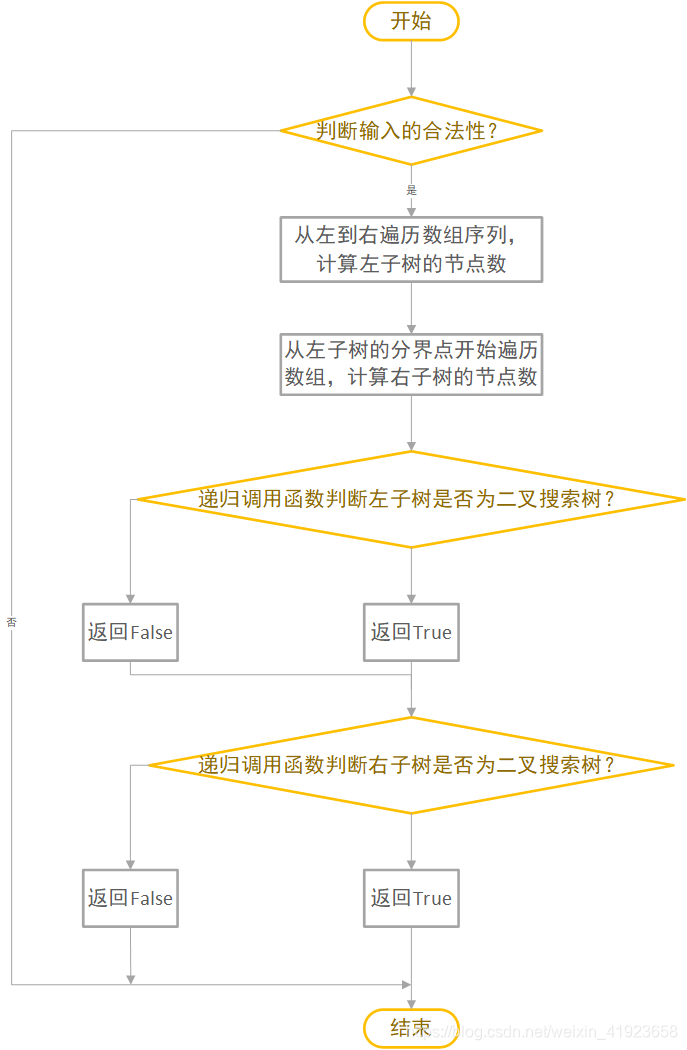
完整代码：

class Solution {
public:
    bool VerifySquenceOfBST(vector<int> sequence) {
        //判断输入的合法性
        if(sequence.empty())
            return false;
        //获取整数数组的长度
        int length = sequence.size();
        //获取根节点
        int root = sequence[length - 1];
        //从左到右遍历数组，计算左子树的节点个数
        int i = 0;
        for(; i < length - 1; ++i)
        {
            //如果某个元素大于根节点
            //则游标i左侧的元素为左子树，i表示左子树的节点数
            if(sequence[i] > root)
                //则跳出
                break;
        }
        //从游标i开始遍历数组，计算右子树的节点个数
        int j = i;
        for( ; j < length - 1; ++j)
        {
            //如果数组中某个元素小于根节点
            if(sequence[j] < root)
                //则表明序列不符合BST
                return false;
        }
        //递归调用函数判断左子树是否是BST
        bool left = true;
        //如果存在左子树，则i必须大于0
        if(i > 0)
        {
            //声明一个左子树容器
            vector<int> leftarray;
            //i表示左子树的节点个数，将左子树的节点压入到左子树容器中
            for(int m = 0; m < i; ++m)
            {
                leftarray.push_back(sequence[m]);
            }
            //判断左子树的节点的值是否小于根节点
            left = VerifySquenceOfBST(leftarray); 
        }
        //递归调用函数判断右子树是否为BST
        bool right = true;
        //如果存在右子树，则i必须小于length-1
        if(i < length - 1)
        {
            //声明一个右子树容器
            vector<int> rightarray;
            //i游标所指的元素为右子树的节点，右子树的节点个数length-i-1
            for(int k = i; k < length - 1; ++k)
            {
                //将右子树的节点压入右子树容器
               rightarray.push_back(sequence[k]); 
            }
            //判断右子树的节点是否大于根节点
            right = VerifySquenceOfBST(rightarray);
        }
        //返回最终的结果
        return (left && right);
    }
};