
根据教工部安排,离散数学的期末考试安排在6月4号下午,也就是考试周第一周的周二下午。
然而不幸的是周一也有一门硬核专业课的考试。。。

~~为了能活过期末考试周,~~决定提前开始复习计划。
先看一眼课程的大纲:

复习就按下面的列表来:
- Logic & Mathematical Proofs 逻辑和证明(Lecture 1-3)
- Sets and Functions 集合与函数
- Complexity of Algorithms 算法复杂度
- Number Theory 数论
- Cryptography 密码学
- Mathematical Induction 数学归纳法
- Recursion 递归
- Counting 计数
- Relations 关系
- Graphs 图
- Trees 树
- Final 期末考试6月4号
王琦老师的课件做得很精致,看得出来老师备课用了很多心思。

Lecture 1 主要是对离散数学这门课的一个概览
开始讲了离散数学的四个经典问题
- Prove that “For an integer n, if 3n + 2 is odd, then n is odd”.
三种证明方法:
direct proof,
proof by contrapositive,
proof by contradiction - Four-color theorem 以及其他图染色问题
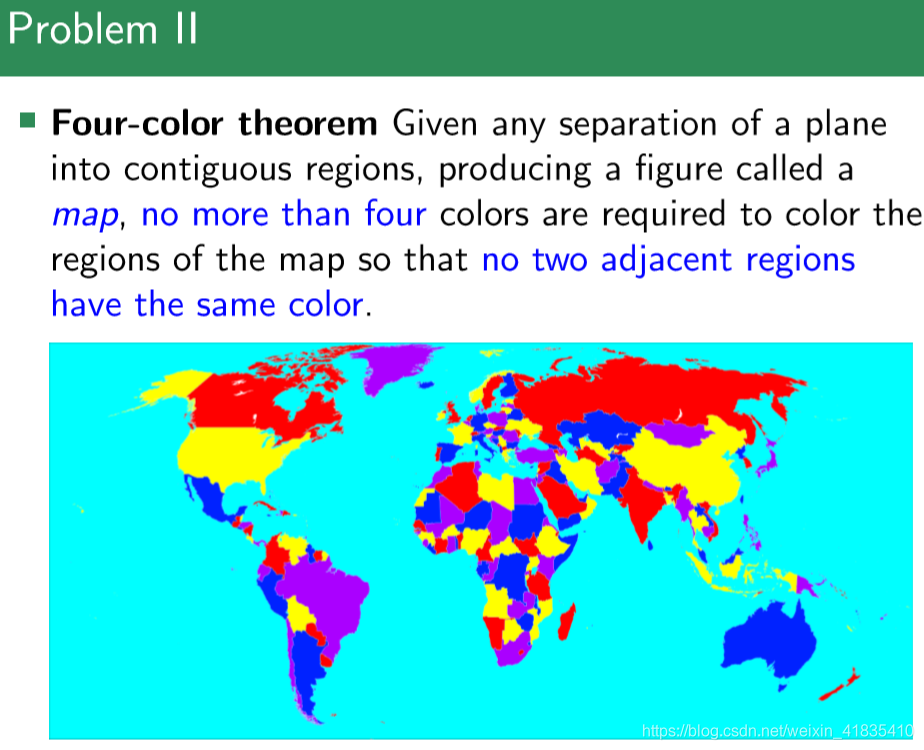
图染色问题的应用
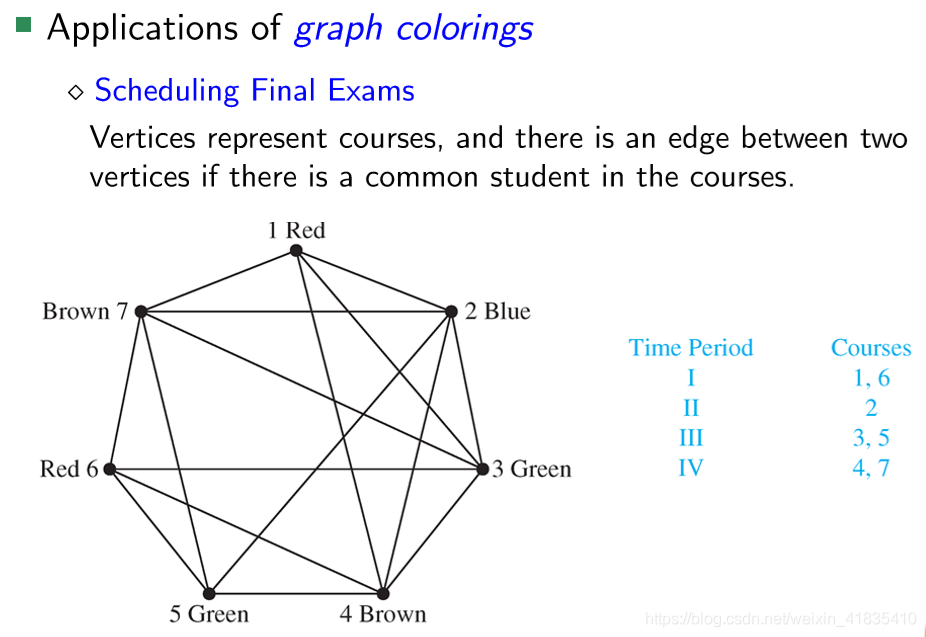
- 七桥问题
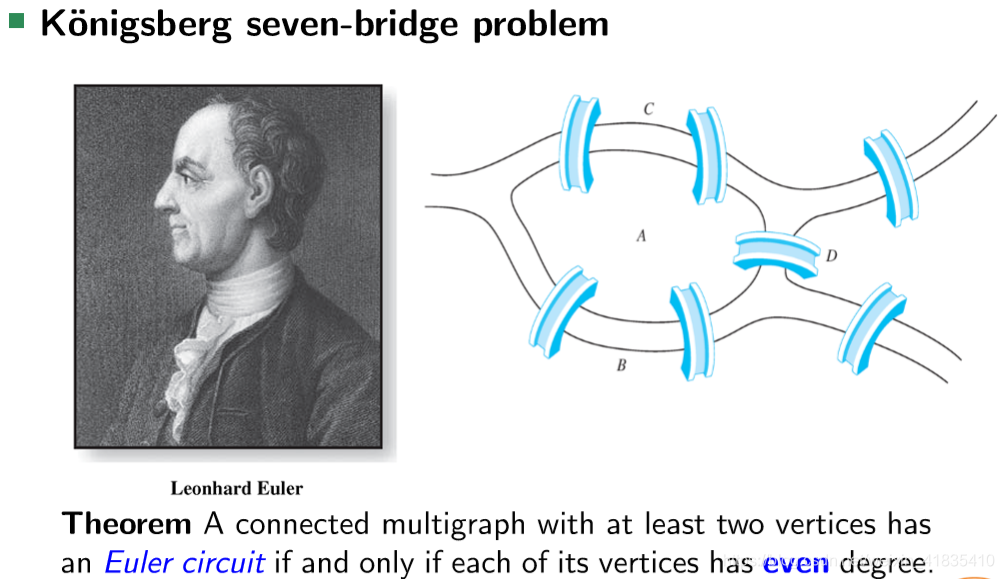
- Fibonacci number
这个数的来源

解的形式

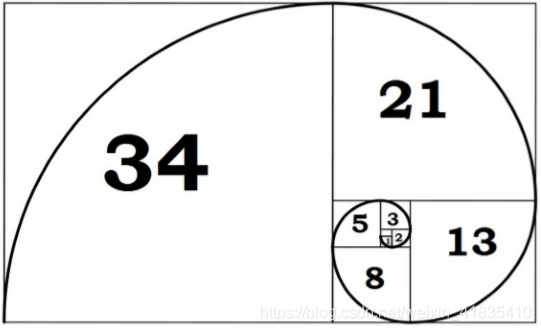
然后就是正式的课程内容复习了。接下来的二十天只剩十天了,争取能文字直播复习过程?








 离散数学期末考试安排在6月4号下午,当天周一还有一门硬核专业课考试。为应对考试周,博主决定提前开始复习,列出了复习大纲,涵盖逻辑和证明、集合与函数等内容,还提及王琦老师课件精致,以及课程中的经典问题和证明方法。
离散数学期末考试安排在6月4号下午,当天周一还有一门硬核专业课考试。为应对考试周,博主决定提前开始复习,列出了复习大纲,涵盖逻辑和证明、集合与函数等内容,还提及王琦老师课件精致,以及课程中的经典问题和证明方法。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








