本文深入探讨线性表的概念、特点及存储方式，包括顺序存储与链式存储，并对比两者差异，旨在帮助读者掌握数据结构中的关键知识点。
写在前面的话：
适应范围：《数据结构》复习总结系列适用于考研、期末考试、考前复习，小白新手
本系列参考书目： 《数据结构：c语言版》（严蔚敏）
关于写这个系列的原因：本人今年考研上岸，加上在校期间学习《数据结构》这门课时候，对数据结构有了好感，对这门课考试的考点把握还不错，所以不想荒废自己的知识，就计划用这种方式总结起来。如果有理解不到位的地方，欢迎在评论指出。我会尽量把知识点讲清楚后，按照考点进行总结。这个系列计划按照知识点总结后+考点总结，同时配有少部分习题（之后会放出大量习题的链接，可以自行练习下载）的方式进行，我会加快更新速度，有不理解的问题也可以在评论提出，大家一起学习进步嗷。
第二章 线性表
本章开始讨论线性结构及其逻辑结构、存储结构和相关运算。线性表作为最基本、最简单、也是最常用的一种数据结构，本章所涉及知识点在接下来的章节学习时也常用到。同时也是数据结构的重点内容。
本章涉及的算法题实现起来较为容易且代码量较少，但需考虑所设计代码的性能，因此要熟知线性表的各种基本操作，务必在本章打好基础。
【考点】①线性表的定义；
②线性表的顺序存储表示；
③线性表的链式存储表示（包括单链表、循环链表、双向链表等）；
④顺序表与链表的比较；
⑤线性表的应用（专门章节进行讲解）
【本章大纲】
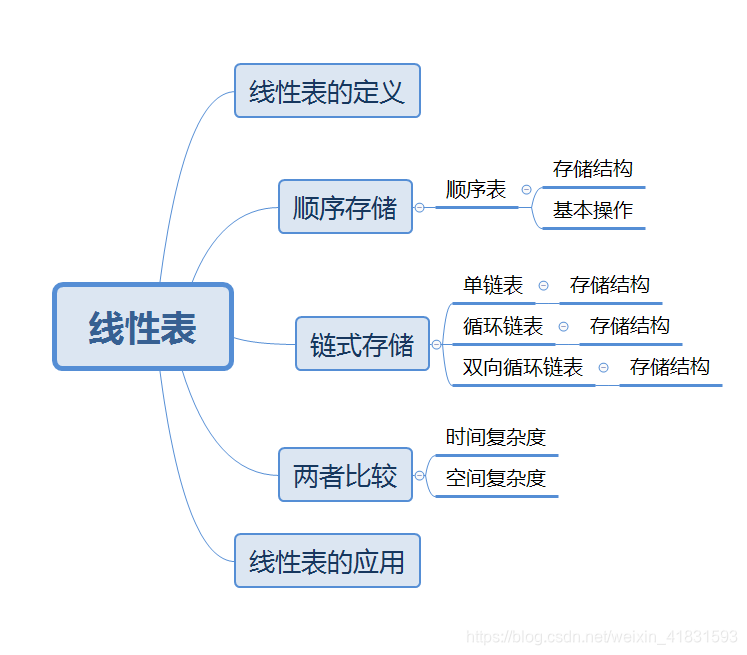
【目录】
一、线性表的定义
1.1 相关概念术语
1.1.1 线性表
【例】在月份表中（1，2，3，.... ，11，12）中就是一个线性表，表中数据元素是单个数字，虽然数据元素的不相同，但他们拥有相同的数据特性。
【定义】如上例子，由n个具有相同特性的数据元素的有限序列称为线性表。
1.1.2 空表
【定义】线性表中元素个数n定义为线性表的长度，当n=0时为空表。
【例】建立一张2022学年学生期末成绩表，而现在还未举行期末考试，不知道学生的成绩，因此此表没有数据元素为一张空表。
1.1.3 相关名词
【例】字母表（A,B,C,D,E,F,G,H）
【定义】在字母表中,A被称为线性起点，H被称为线性终点。以C而言，B为起直接前驱，D为其直接后继。
1.2 线性表的特点
（1）集合中必存在唯一的一个“第一元素”。
（2）集合中必存在唯一的一个 “最后元素” 。
（3）除最后一个元素之外，均有唯一的后继。
（4）除第一个元素之外，均有唯一的前驱。
二、线性表的顺序存储
2.1 顺序表示相关概念
【定义】顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素，称为线性表的顺序存储结构）。通常使用这种存储结构的线性表被称为顺序表，它的特点为逻辑上相邻的数据元素，在物理位置上也是相邻的。
【例】
如图，只要确定了存储线性表的起始位置，线性表中的任一元素的位置都可随机存取。因此，线性表的顺序存储结构是一种随机存取。
2.2 顺序表的存储结构表示
【算法描述】
#define MAXSIZE 100; //声明顺序表的最大长度
typedef struct {
ElemType *elem; //线性表的基地址（初始地址）
int Length; //顺序表的长度
}SqList;
2.3 顺序表中基本操作的实现
2.3.1 顺序表的初始化
【算法思想】①为顺序表L分配一个maxsize大小的数组康健，并使基地址指向此空间的基地址
②将表的长度置为0，即置为空表
【算法描述】
status InitList (SqList &L){
L.elem = new ElemType[MAXSISE]; //为顺序表分配一个maxsize大小的空间
if (!L.elem) exit (OVERFLOW); //存储分配失败
L.length=0; //设置空表长度为0
return OK;
}2.3.2 顺序表的取值
【算法思想】判段取值位置 i 是否合法
①合法时，将第i 个元素即L.elem[i-1]所对应的值赋给参数e，使参数e返回数据元素 i 的值；
②不合法时，返回EROR。
【算法分析】查找操作是根据指定元素位置进行查找的，因此取值算法的时间复杂度为O(1)。
【算法描述】此算法也体现出顺序表的随机存取的特点。
int GetElem(SqList L,int i,ElemType &e)
{
if (i<1||i>L.length) return ERROR; //判断i值是否合理，若不合理，返回ERROR
e=L.elem[i-1]; //第i-1的单元存储着第i个数据
return OK;
}
2.3.3 顺序表的查找
【算法思想】当查找数字时，如图
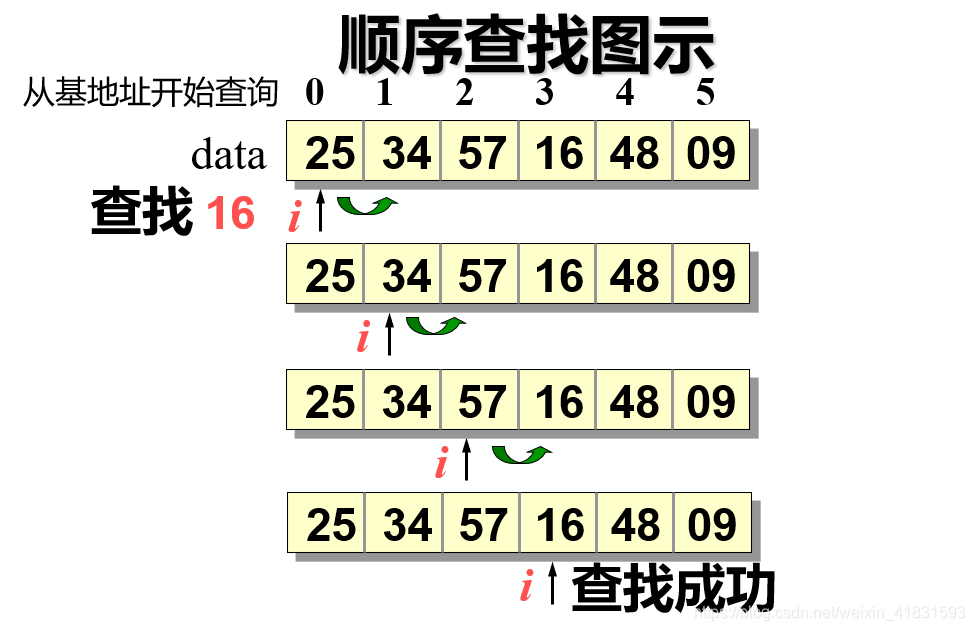
若查找数字66，依旧从初始地址进行查找，向后逐一查询，直至查找到最后一个元素，依旧不符合时，返回ERROR。
【算法分析】通过上图中的示例，可以看出顺序表上查找一个数据元素，其时间主要消耗在比较数据上，而比较数据元素的次数取决于所要插入的位置，假设在等概率情况下每个元素被查找到的概率为1/n，因此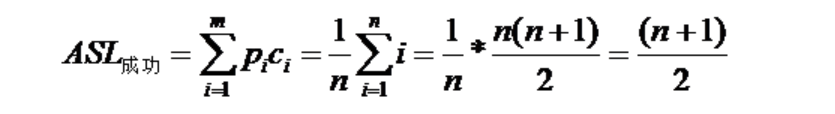
所以，顺序表按值查找算法的时间复杂度为O(n)。
【算法描述】
int LocateELem(SqList L,ElemType e)
{
for (i=0;i< L.length;i++)
if (L.elem[i]==e) return i+1; //查找成功，返回其序号
return ERROR; //查找失败，返回ERROR
}
2.3.4 顺序表的插入
【算法思想】(1)判断插入位置i是否合法；判断顺序表的存储空间是否已满。
(2)将第n至第i位的元素依次向后移动一一个位置，空出第i个位置，如下图。
(3)将要插入的新元素e放入第i个位置。
(4)表长加1,插入成功返回OK。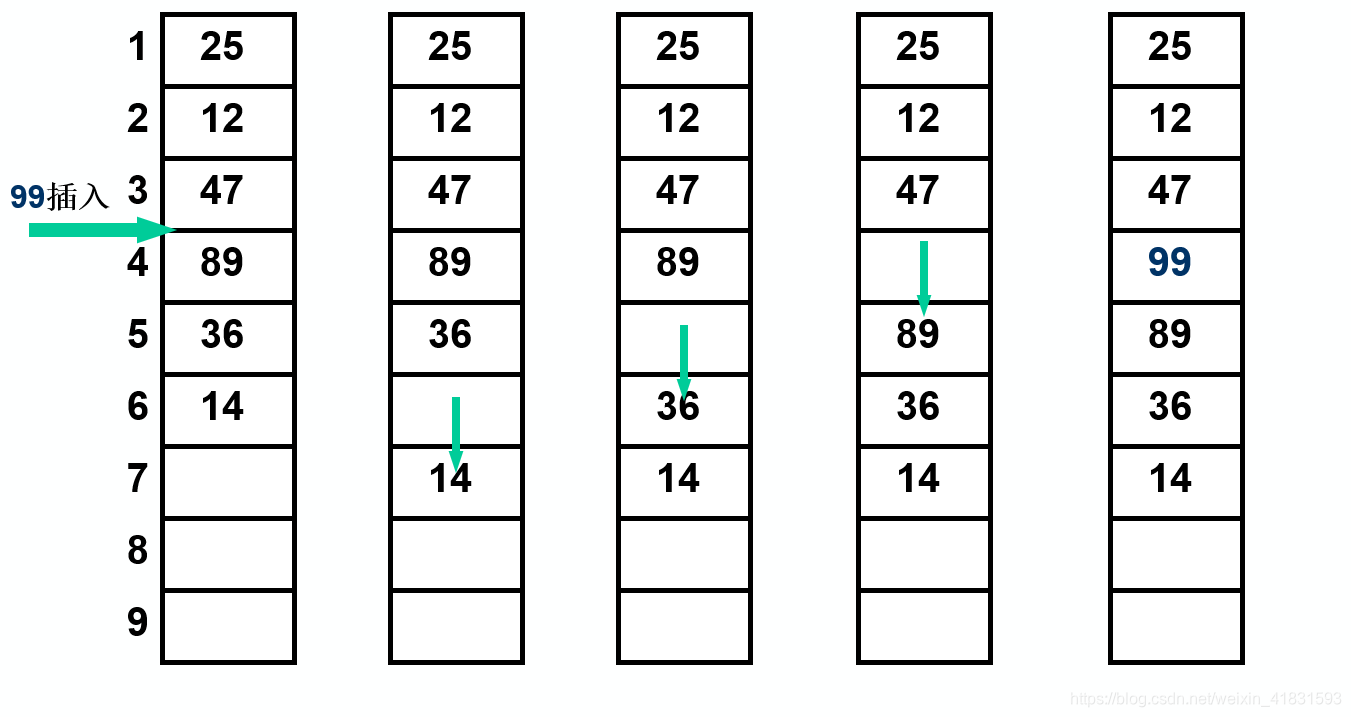
【算法分析】 通过上图中的示例，可以看出顺序表上插入一个数据元素的主要特点是先移动后插入，因此时间主要消耗在移动数据上，而移动数据元素的次数取决于所要插入的位置。据观察，插入第i个元素的位置，需要移动n-i+1次。
假设在等概率情况下每个位置被插入的概率为1/（n+1），其n+1是因为元素除了插入在n个元素的位置，还有可能直接插入最后一个元素的后面，所以有n+1种可能性。
因此平均移动次数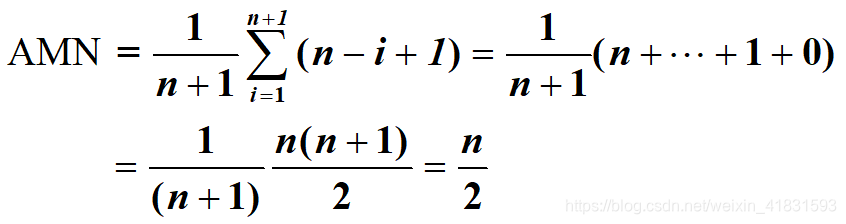
所以，顺序表的插入算法的时间复杂度为O(n)。
【算法描述】
Status ListInsert_Sq(SqList &L,int i ,ElemType e){
if(i<1 || i>L.length+1) return ERROR; //i值不合法
if(L.length==MAXSIZE) return ERROR; //当前存储空间已满
for(j=L.length-1;j>=i-1;j--)
L.elem[j+1]=L.elem[j]; //插入位置及之后的元素后移
L.elem[i-1]=e; //将新元素e放入第i个位置
L.length++; //表长增1
return OK;
}
2.3.5 顺序表的删除
【算法思想】(1)判断删除位置i是否合法(合法值为1si≤n)。
(2)将欲删除的元素保留在e中。
(3)将第i+ 1至第n位的元素依次向前移动一个位置。
(4)表长减1，删除成功返回OK。
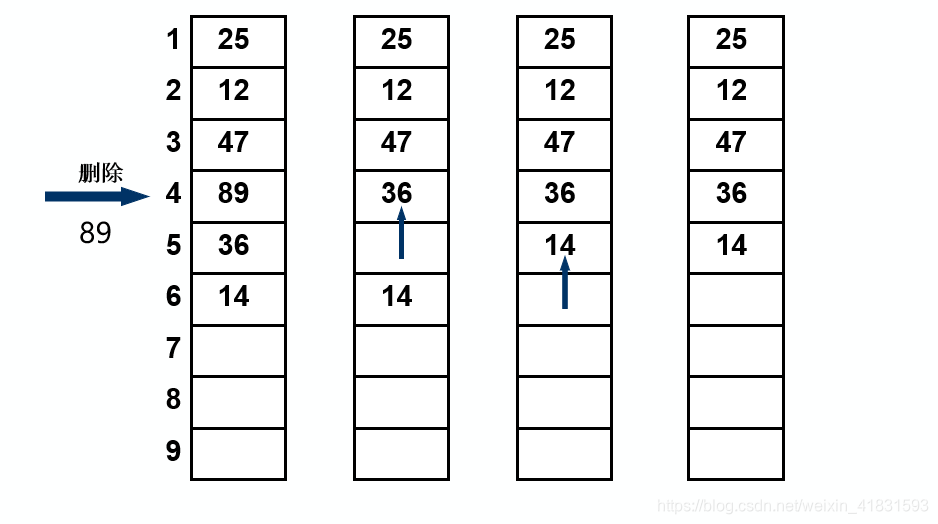
【算法分析】 通过上图中的示例，可以看出顺序表上删除一个数据元素的主要特点是先删除后移动，因此时间主要消耗也在移动数据上，而移动数据元素的次数取决于所要删除元素的位置。据观察，插入第i个元素的位置，需要移动n-i次。
假设在等概率情况下每个位置被插入的概率为1/n。因此平均移动次数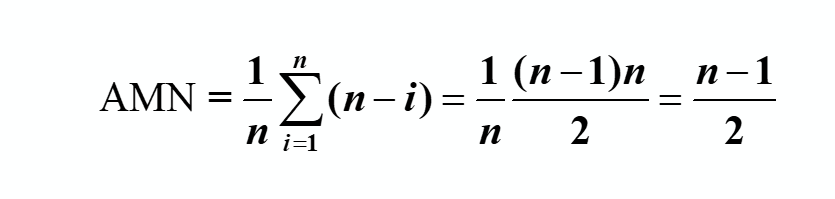
所以，顺序表的插入算法的时间复杂度为O(n)。
【算法描述】
Status ListDelete_Sq(SqList &L,int i，Elemtype e){
if((i<1)||(i>L.length)) return ERROR; //i值不合法
e=L.elem[i];
for (j=i;j<=L.length-1;j++)
L.elem[j-1]=L.elem[j]; //被删除元素之后的元素前移
L.length--; //表长减1
return OK;
}
三、线性表的链式存储
3.1 单链表链式表示的相关概念
3.1.1 结点
在链式存储结构中，为了表示每个数据元素aᵢ与其直接后继元素aᵢ₊₁之间的逻辑关系，对于数据元素aᵢ而言，除了存储其本身的信息之外，还需存储一个指其直接后继的信息（直接后继的存储位置）。
由这两部分信息组成的数据元素aᵢ的存储映像，称为结点。每个结点包括两个域：
3.1.2 链式存储结构
【定义】n个结点链结成一个链表，即为线性表的链式存储映像，也称为线性表的链式存储结构。
【特点】①相邻结点在存储器中的位置是任意的（可以是连续的，也可以是不连续的），即逻辑上相邻的数据元素在物理上不一定相邻。
②整个链表的存取必须从头指针开始进行，从前到后依次遍历，也成为顺序存取的存取结构。
【例】结点之间的箭头表示链域中的指针
【优点】①数据元素的个数可以自由扩充；
②插入、删除等操作不必移动数据，只需修改链接指针。
【缺点】①存储密度小；
②存储效率不高，必须采用顺序存取，即存取数据元素时，只能按链表的顺序进行访问。
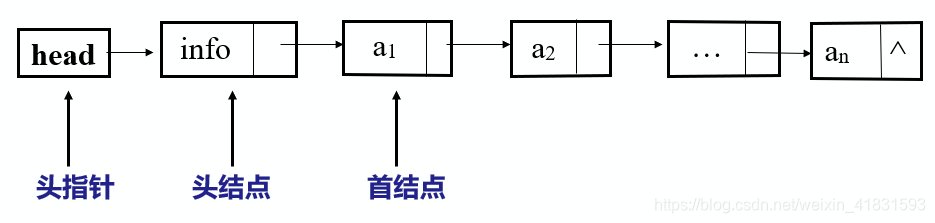
3.1.3 首元结点、头结点、头指针的区分
①头指针是指向链表中第一个结点的指针；
②头结点是在链表的首元结点之前附设的一个结点；数据域内只放空表标志和表长等信息；
③首结点是指链表中存储第一个数据元素a1的结点。
3.1.4 其他说明
①单链表是由表头指针唯一确定的，因此单链表可以用头指针的名字命名。如头指针的名为head，则检测此链表为表head。
②在链表头增加头结点主要有两个作用：
第一，便于首元结点的处理（首结点的地址保存在头结点的指针域中,所以在链表的第一个位置上的操作和其它位置一致，无须进行特殊处理）;
第二，便于空表和非空表的统一处理（无论链表是否为空，头指针都是指向头结点的非空指针，因此空表和非空表的处理也就统一了）。
③注意区分指针变量和结点变量两个不同的概念。指针变量p：表示结点地址；结点变量*p：表示一个结点的值
3.2 单链表的存储结构表示
【算法描述】
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList; // *LinkList为Lnode类型的指针
3.3 单链表中基本操作的实现
3.3.1 单链表的初始化
【算法思想】（1）生成新结点作头结点，用头指针L指向头结点。
（2）头结点的指针域置空。
【算法描述】
Status InitList_L(LinkList &L){
L=new LNode; //生成新节点作为头结点
L->next=NULL; //头结点的指针域置空
return OK;
}
3.3.2 单链表的取值（根据位置）
【算法思想】对于链表的查找，要从链表的头指针出发，顺着链域next逐个结点往下搜索，直至搜索到第i个结点为止，所以链表不是随机存取结构，取值步骤如下：
（1）从L->next顺链扫描，用指针p指向当前扫描到的结点，p初值p = L->next。
（2）j 做计数器，累计当前扫描过的结点数，j 初值为1。
（3）当p指向扫描到的下一结点时，计数器j 加1。当j = i时，p所指的结点就是要找的第i个结点；当P=NULL时，取值失败。
【算法分析】
该算法的主页操作为比较 i 与 j 并后移指针 p 。而while循环体中的语句频度主要与位置 i 有关。
假设在等概率情况下，每个元素的取值概率相等，即都为1/n。①当1≤ i ≤ n时，频度为 i - 1，取值成功；②若 i>n,则频度为n，取值失败。因此改算法最坏时间复杂度为O(n)。
平均查找长度ASL=(n-1)/2，因此平均时间复杂度为O(n)。
【算法描述】
Status GetElem_L(LinkList L,int i,ElemType &e){
p=L->next;j=1; //初始化
while(p&&j<i){ //向后扫描，直到p指向第i个元素或p为空
p=p->next; ++j;
}
if(j==i)
e=p->data; //取第i个元素的数据域
else
return ERROR; //第i个元素不存在
return OK;
}3.3.3 单链表的按值查找
【算法思想】从第一个结点起，依次和e相比较：
（1）如果找到一个其值与e相等的数据元素，则返回其在链表中的“位置”或地址；
（2）如果查遍整个链表都没有找到其值和e相等的元素，则返回0或“NULL”。
【算法分析】
该算法的执行时间与待查找的值e相关，类似于单链表的取值，因此时间复杂度也为O(n).
【算法描述】
LNode *LocateELem_L (LinkList L，Elemtype e) {
LNode *p;
p=L->next; //初始化，p指向首元结点
while(p &&p->data!=e) //顺序扫描
p=p->next; //p指向下个结点
return p; //查找成功返回值为e的结点地址p，查找失败p为null
}
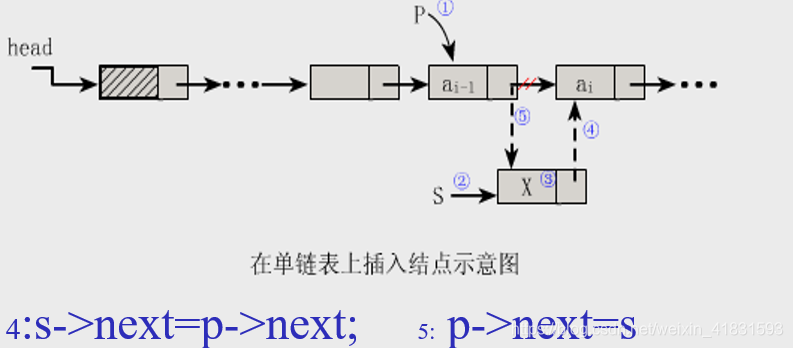
3.3.4 单链表的插入（⭐⭐⭐）
【算法思想】此算法应注意指针指向顺序，避免造成断链：
（1）找到ai-1存储位置p(插入点的直接前驱)(图步骤①) ;
（2）生成一个新结点*s (图步骤②);
（3）将新结点*s的数据域置为x(图步骤③);
（4）新结点*s的指针域指向结点ai (图步骤④);
（5）令结点*p的指针域指向新结点*s (图步骤⑤)。
【算法分析】此算法需要在插入第 i 个结点之前，先找的第 i-1 个结点，因此也需顺序找到此结点的位置，其时间复杂度与单链表的取值算法相同为O(n)。
【算法描述】
Status ListInsert_L(LinkList &L,int i,ElemType e){
p=L;j=0;
while(p&&j<i−1){p=p->next;++j;} //寻找第i−1个结点，使p结点指向该结点
if(!p||j>i−1)return ERROR; //i大于表长 + 1或者小于1,位置不合理
s=new LNode; //生成新结点*s
s->data=e; //将结点*s的数据域置为e
s->next=p->next; //将结点*s的指针域指向结点ai
p->next=s; //将结点*p的指针域指向结点*s
return OK;
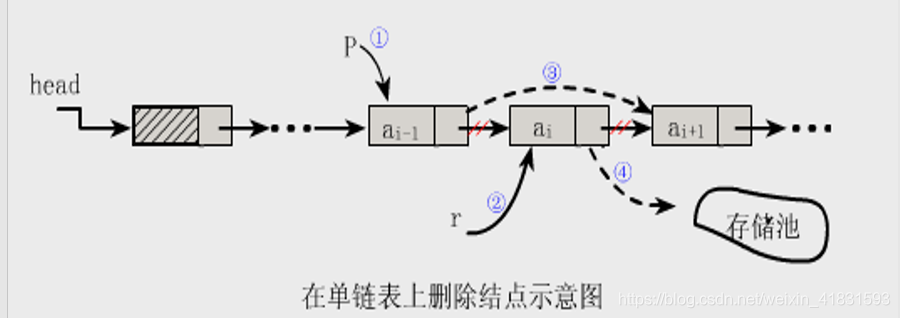
}//3.3.5 单链表的删除（⭐⭐⭐）
【算法思想】（1）找到ai-1存储位置p(删除结点的直接前趋)(图步骤①)；
（2）保存要删除的结点的值(图步骤②)；
（3）令p-＞next指向ai的直接后继结点(图步骤③)；
（4）释放结点ai的空间(图步骤④)。
【算法分析】此算法同样也类似于插入算法，时间复杂度也为O(n)。
【算法描述】
Status ListDelete_L(LinkList &L,int i,ElemType &e){
p=L;j=0;
while(p->next &&j<i-1){ //寻找第i-1个结点，并令p指向该结点
p=p->next; ++j;
}
if(!(p->next)||j>i-1)
return ERROR; //删除位置不合理
q=p->next; //临时保存被删结点的地址以备释放
e=q->data; //保存删除结点的数据域
p->next=q->next; //改变删除结点前驱结点的指针域
delete q; //释放删除结点的空间
return OK;
}3.3.6 单链表的创建（⭐⭐⭐）
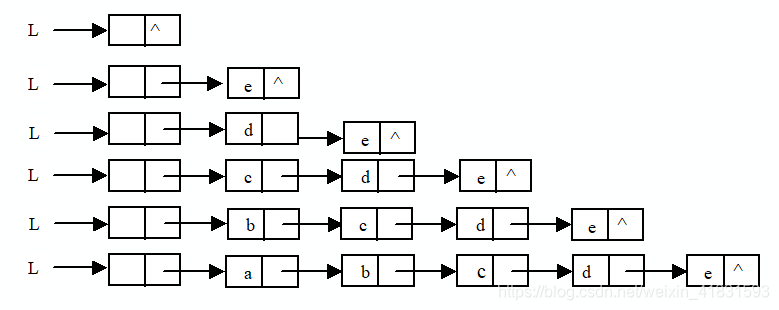
① 前插法创建单链表
【算法思想】从一个空表开始，重复读入数据：
(1)生成新结点；
(2)将读入数据存放到新结点的数据域中；
(3)将该新结点插入到链表的前端。
【算法分析】当有n个数据时，需插入n次，因此时间复杂度为O(n)。
【算法描述】
void CreateList_F(LinkList &L,int n){
L=new LNode;
L->next=NULL; //先建立一个带头结点的单链表
for(i=n;i>0;--i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=L->next;
L->next=p; //将新结点*p插入到头结点之后
}
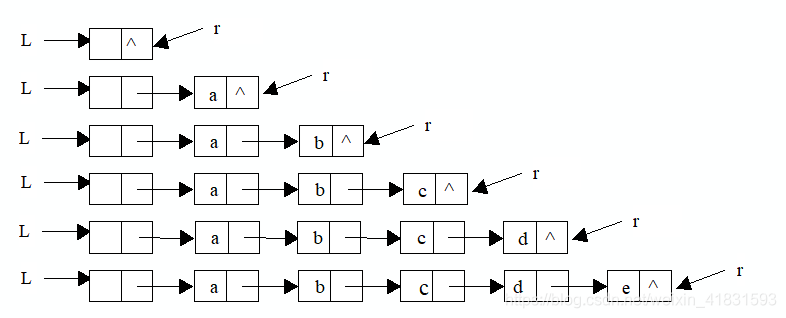
}② 后插法创建单链表
【算法思想】
(1)从一个空表L开始，将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点。
(2)初始时，r同L均指向头结点。每读入一个数据元素则申请一个新结点，将新结点插入到尾结点后，r指向新结点。
【算法分析】当有n个数据时，需插入n次，因此时间复杂度为O(n)。
【算法描述】
void CreateList_L(LinkList &L,int n){
L=new LNode;
L->next=NULL;
r=L; //尾指针r指向头结点
for(i=0;i<n;++i){
p=new LNode; //生成新结点
cin>>p->data; //输入元素值
p->next=NULL; r->next=p; //插入到表尾
r=p; //r指向新的尾结点
}
}3.3 循环链表
【特点】表中最后一个结点的指针域指向头结点，整个链表如同一个环形。正是这样的结构，我们可以从任意一个结点找到表中其他的结点。
【注意】
(1)循环链表与单链表在大多数情况下的操作是相同的，两者的差别在于：
当单链表在遍历时判断当前指针p是否指向表尾结点的终止条件为p ！=null 或p->next！=null；而循环链表为p！=L或p->next !=L。
(2)对循环链表，有时不给出头指针，而给出尾指针,可以更方便的找到第一个和最后一个结点。
3.4双向链表
3.4.1 双向链表的相关概念
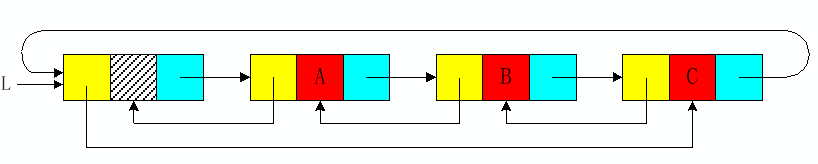
【特点】在双向链表中，每个结点pᵢ拥有两个指针域，一个指向直接后继（pᵢ->next），另一个指向直接前驱(pᵢ->prior)。正是这种结构，在查找某个结点的直接前驱不在需要从头遍历。
【注意】B->next->prior = B->prior->next = B
3.4.2 双向链表的插入（⭐⭐⭐）
【算法思想】注意不要因为步骤不对，造成断链问题。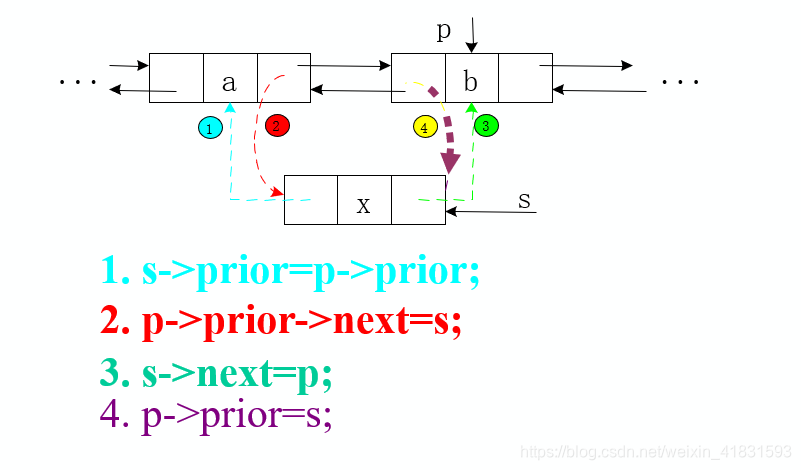
【算法描述】
Status ListInsert_DuL(DuLinkList &L,int i,ElemType e){
if(!(p=GetElemP_DuL(L,i)))
return ERROR; //确定第i个元素的位置指针p
s=new DuLNode; //生成新节点*s
s->data=e; //将结点*s的数据域置为e
s->prior=p->prior; //将结点*S插入L中，对应图中步骤①
p->prior->next=s; //对应图中步骤②
s->next=p; //对应图中步骤③
p->prior=s; //对应图中步骤④
return OK;
}
3.4.3 双向链表的删除（⭐⭐⭐）
【算法思想】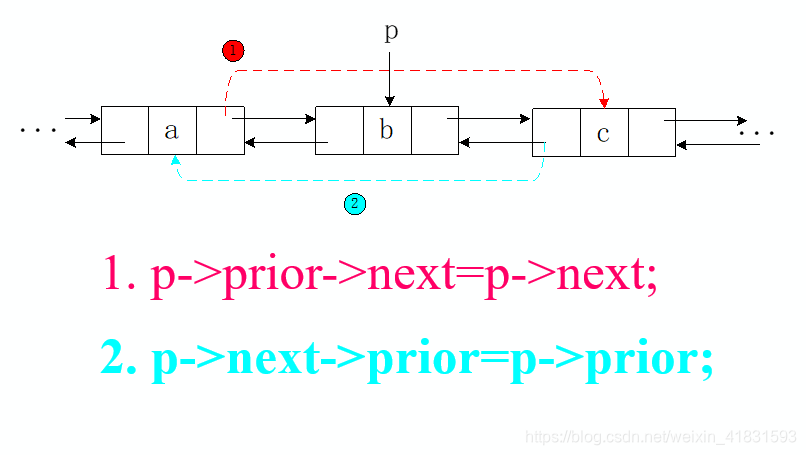
【算法描述】
Status ListDelete_DuL(DuLinkList &L,int i,ElemType &e){
if(!(p=GetElemP_DuL(L,i))) //确定第i个元素的位置指针p
return ERROR;
e=p->data;
p->prior->next=p->next; //修改被删除结点的前驱结点的后继指针
p->next->prior=p->prior; //修改被删除结点的后继结点的前驱指针
delete p; //释放空间
return OK;
}
四、顺序表与链表的比较
| 存储结构 | 顺序表 | 链表 | |
|---|---|---|---|
| 空间 | 存储空间 | 预先分配，会导致空间闲置或溢出现象 | 动态分配，不会出现存储空间闲置或溢出现象 |
| 存储密度 | 不用为表示结点间的逻辑关系而增加额外的存储开销，存储密度等于1 | 需要借助指针来体现元素间的逻辑关系，存储密度小于1 | |
| 时间 | 存取元素 | 随机存取，按位置访问元素的时间复杂度为O(1) | 顺序存取，按位置访问元素时间复杂度为O(n) |
| 插入、删除 | 平均移动约表中一半元素，时间复杂度为O(n) | 不需移动元素，确定插入、删除位置后，时间复杂度为O(1) | |
| 适用情况 | ① 表长变化不大，且能事先确定变化的范围 ② 很少进行插入或删除操作，经常按元素位置序号访问数据元素 | ① 长度变化较大 ② 频繁进行插入或删除操作 | |
【注】①存储密度为数据元素本身所占用的存储量与整个结点结构所占用的存储量之比。
②两种存储方式各有优缺点，对于频繁进行插入删除操作的线性表，宜采用链表作为存储结构；为节约存储空间，宜采用顺序表作为存储结构。
扫一扫
2509
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
