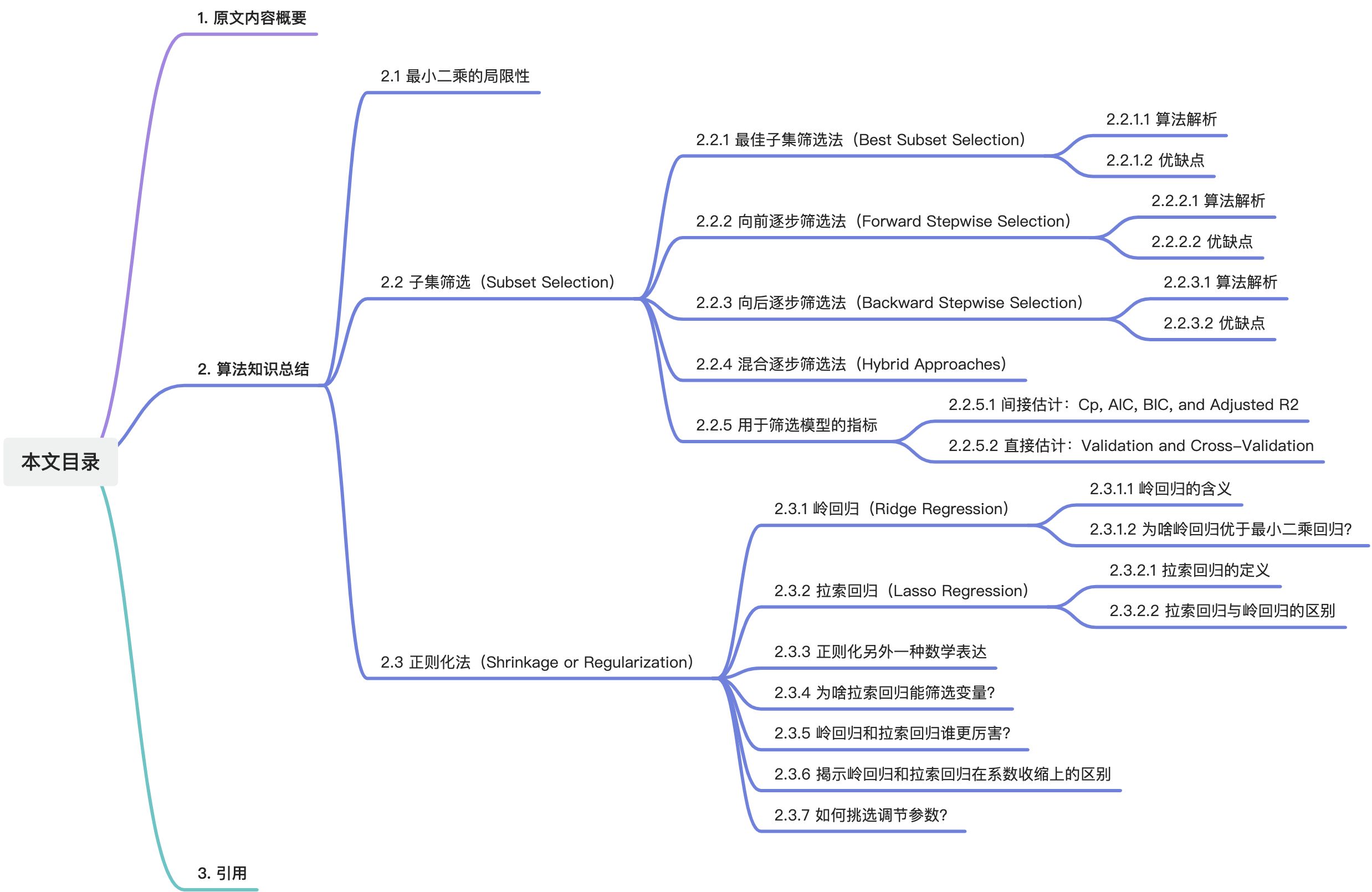
目录
1. 原文内容概要
在数据的宇宙里,构建机器学习模型犹如在夜空中绘制星座,既需精确又求优雅。但这片宇宙并非一望无际的清晰,充满了噪声和冗余的迷雾。为了揭开数据深处的秘密,我们必须进行一场艺术之旅——筛选出有价值的变量(Subset Selection)、用正则化雕塑模型(Shrinkage Methods)、通过降维探寻低维空间的奥秘(Dimension Reduction Methods)。
本篇读书笔记将带你深入这场机器学习中的模型炼金术,揭秘如何在复杂与简洁之间雕刻出平衡,将混沌的数据雕琢成洞察力强、预测精准的模型。
由于内容较多,第六章的读书笔记会分成【上】、【下】两部分输出。【上】部分将介绍“子集筛选”和“正则化”,【下】将介绍“降维”方法。
2. 算法知识总结
2.1 最小二乘的局限性
大家先回忆下线性模型的基本表现形式:
线性模型虽然简单,但现实生活中用处非常广泛。拟合线性模型最基础的方法当属“最小二乘法”,这种方法理解起来特别顺畅,但经常会用不上劲(变量数大于样本数时)和用力过猛(过拟合的情况)。为了提高线性模型的拟合质量,有必要对“最小二乘法”进行一些优化改进。
具体来讲,可以从两个方面来探究最小二乘法的局限性:
1)预测精度方面:如果自变量和因变量之间近似线性相关,并且样本量显著多于变量数,那么使用最小二乘法可以构建一个精确度较高的模型。然而,在样本量与变量数相差不大的情况下,该模型容易发生过拟合现象(However, if n is not much larger than p, then there can be a lot of variability in the least squares fit, resulting in overfitting and consequently poor predictions on future observations not used in model training)。当样本量少于变量数量时,最小二乘法将无法得出唯一解,因此变得无效(And if p > n, then there is no longer a unique least squares coefficient estimate: there are infinitely many solutions)。在这种情况下,存在多个解可以使训练误差降至零,导致极端的过拟合现象。
2)模型解释方面:在使用线性模型时,很多自变量可能与因变量无关。为了剔除这些无关变量(也就是将对应的变量系数变为 0 0 0),降低模型复杂度并提高可解释性,我们需要采用特定的变量选择算法。由于最小二乘法本身不具备变量筛选功能,所以必须借助其他算法来实现这一目的(Now least squares is extremely unlikely to yield any coefficient estimates that are exactly zero)。
由此引出子集筛选、正则化、降维等优化方法。
2.2 子集筛选(Subset Selection)
2.2.1 最佳子集筛选法(Best Subset Selection)
2.2.1.1 算法解析
这种方法采用了一种直接而全面的策略,即尝试每一种可能的组合方式,进而从中筛选出最优解。具体操作步骤可以概括为以下三点,我们以线性回归问题为例来说明:
1) M 0 M_0 M0是一个初始模型(null model),不含有任何解释性变量。由于缺乏预测因子,该模型的预测策略简化为使用数据集的整体均值作为每个预测点的输出。
2)设定 k k k的取值范围为 1 , 2 , … p 1,2,…p 1,2,…p,其中 p p p表示可用变量的总数, k k k表示在当前循环迭代中,模型所包含的变量数量。对于每个 k k k值,遍历所有可能的变量组合,并为每种组合拟合相应的模型(即下图中的步骤a);接着,使用一个评估模型性能的指标(例如残差平方和 R S S RSS RSS或决定系数 R 2 R^2 R2)来挑选出表现最佳的模型,将其标记为 M k M_k Mk(即下图中的步骤b)。通过这一过程,加上最初得到的初始模型 M 0 M_0 M0,最终得到了 p + 1 p+1 p+1个候选模型。
3)针对上一步的 p + 1 p+1 p+1个模型,将它们放在独立的验证集上进行预测,再根据衡量模型精度的指标选出最优秀的那一个。
下文中最佳子集筛选法简称best方法。
2.2.1.2 优缺点
这种方法的优点是易理解,缺点就是难计算。对于 p p p个待筛变量来说,我们一共会拟合 2 p 2^p 2p种不同的变量组合。当变量数量超过40个时,即便是性能强大的计算机也会无能为力(Consequently, best subset selection becomes computationally infeasible for values of p greater than around 40, even with extremely fast modern computers)。
另一个不利之处是,随着搜索空间的扩大,模型过拟合的风险也随之增加(The larger the search space, the higher the chance of finding models that look good on the training data, even though they might not have any predictive power on future data. Thus an enormous search space can lead to overfitting and high variance of the coefficient estimates)。
由此引出逐步筛选法。
2.2.2 向前逐步筛选法(Forward Stepwise Selection)
2.2.2.1 算法解析
这个算法理解起来比较绕,分为以下几步,以线性回归问题为例:
1) M 0 M_0 M0为不含有任何变量的初始模型(null model);
2)首先设定 k k k的取值范围为 0 , 1 , … , p − 1 0, 1, \ldots, p-1 0,1,…,p−1,其中 p p p表示可选变量的总数。这里的 k k k并不代表模型中的实际变量数,而是表示迭代的轮次。对于每个 k k k值,我们执行以下操作:
- 当 k = 0 k=0 k=0时,我们从不含任何额外变量的初始模型 M 0 M_0 M0出发,逐一添加变量(每次增加一个),由于有 p p p个可选变量,我们将得到 p p p个一元模型。根据模型的评价指标(通常使用 R S S RSS RSS或 R 2 R^2 R2),从这 p p p个模型中选出性能最优的一个,这个模型被视为本轮选择的最佳模型,记作 M 1 M_1 M1。
- 当 k = 1 k=1 k=1时,由于上一轮已经选定了一个变量,剩余可选变量数为 p − 1 p-1 p−1。此时在 M 1 M_1 M1的基础上再次逐一添加变量,将产生 p − 1 p-1 p−1个二元模型。利用评价指标从中选出最优模型,并将其标记为 M 2 M_2 M2。
- 依此规律继续操作,每轮结束后已选变量不参与后续选择。直到完成 k = p − 1 k=p-1 k=








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








