EM最大期望算法

EM最大期望算法

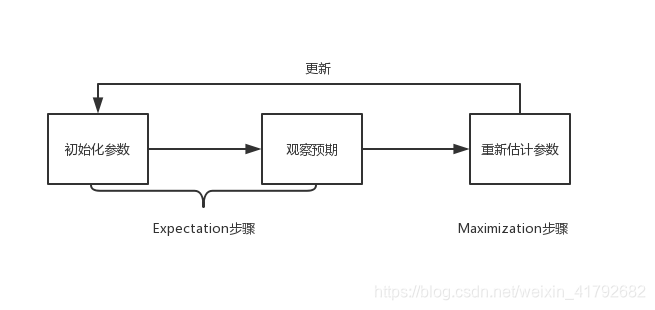
EM算法是一种求解最大似然估计的方法，通过观测样本，来找出样本的模型参数。最大似然估计是一种通过已知结果，估计参数的方法。

EM算法中的E步骤就是通过旧的参数来计算隐藏变量，M步骤是通过得到的隐藏变量的结果来重新估计参数，直到参数不再发生变化。

EM聚类在求解的过程中每个样本都有一定的概率和每个聚类相关，叫做软聚类算法。

常用的EM聚类有GMM高斯混合模型和HMM隐马尔科夫模型。

假设样本是符合高斯分布，个高斯分布都属于这个模型的组成部分（component），要分成K类就相当于是K个组成部分。这样我们可以先初始化每个组成部分的高斯分布的参数，然后再看来每个样本是属于哪个组成部分，即为E步骤，再通过得到的这些隐含变量结果，反过来求每个组成部分高斯分布的参数，即M步骤。反复EM步骤，直到每个组成部分的高斯分布参数不变为止。

GMM是通过概率密度来进行聚类，聚成的类符合高斯分布（正态分布）。而HMM用到了马尔可夫过程，通过状态转移矩阵来计算状态转移的概率。

在EM这个框架中，E步骤相当于是通过初始化的参数来估计隐含变量。M步骤就是通过隐含变量反推来优化参数。最后通过EM步骤的迭代得到模型参数。

sklearn中EM工具包的调用：

from sklearn.mixture import GaussianMixture

GMM聚类的创建：

gmm = GaussianMixture(n_components=1, covariance_type=‘full’, max_iter=100)

1. n_conponents:高斯混合模型的个数，默认为1
2. covariance_type：协方差类型。一个高斯混合模型的分布是由均值向量和协方差矩阵决定的，所以协方差的类型也代表了不同的高斯混合模型的特征。协方差类型有4种取值：
   • covariance_type=full，完全协方差，即元素都不为0
   • covariance_type=tied,相同的完全协方差
   • covariance_type=diag,对角协方差
   • covariance_type=spherical,球面协方差，非对角为0，对角完全相同，呈现球面特性。
3. max_iter:最大迭代次数，默认100

示例利用EM算法对王者荣耀英雄数据进行聚类：

原始数据：

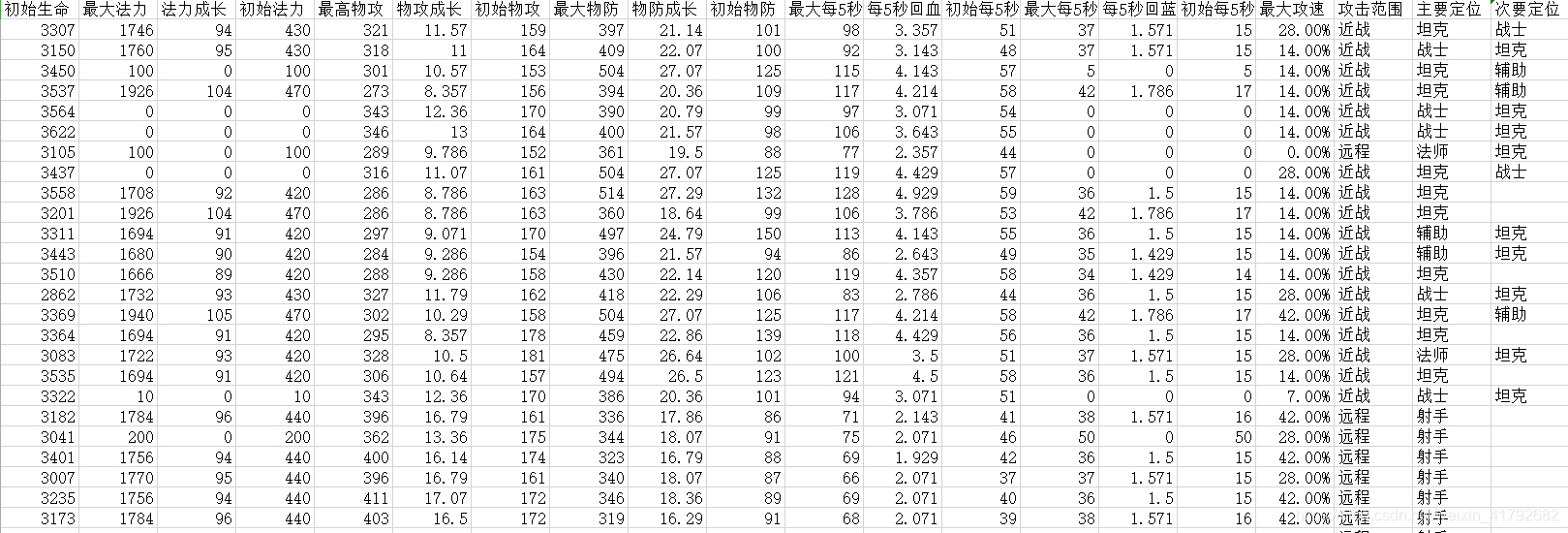
加载数据：

import pandas as pd
import csv
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.mixture import GaussianMixture