在现实世界中,刚体与刚体由于接触力的作用是不可能发生穿透的,但是在物理动画世界,由于我们无法直接得到刚体与刚体的接触力,并且数据模型也很难具备现实世界的刚体属性。所以我们允许模型与模型之间发生穿透,这样我们就可以计算物体与物体之间的接触力,以此来进一步算出物体下一步的运动状态。
基于穿透的物理模拟实际上是一个利用弹簧-阻尼系统来求取碰撞力的方法。
刚体运动基础
在计算机物理模拟中,对于刚体运动通常使用常微分方程来进行描述,也就是常说的ODE。经常使用的ODE有两种,一种叫做Largrangian formulation,另一种是Hamiltonian formulation。
Largrangian formulation
Largrangian formulation是对刚体的位置(r),刚体的姿态四元数(q),刚体的速度(v)与刚体的角速度(ω)进行求导,来构造ODE

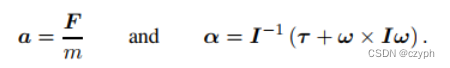
Hamiltonian formulation
Hamiltonian formulation,大体上与Largrangian formulation一致,只不过用动量(P)与角动量(L)来代替速度与角速度,这样做的原因是由于动量守恒,所以可以写出更简单的方程


在解决了OED方程的形式之后,我们需要考虑,如何构造出任意时刻刚体的OED方程。在每一帧的计算中,刚体的位置与刚体的姿态,对于我们来说都是已知的,那么重点就是求刚体的合外力与合外力矩。
一个刚体所受的和外力应该是外力与它与其它刚体碰撞产生的碰撞力的和,同理合外力矩也应该是这样。

在Penalty-Based中我们将碰撞里以穿透产生的弹簧力来表示

在一个仿真循环中,通常可以分为三步
1.运行碰撞检测,求出刚体与刚体与刚体之间的接触点
2.计算穿透力
3.求解ODE,来计算下一步的刚体运动状态。
对于物体 j 来说,他受到的接触力是由于与它发生碰撞的物体 i 产生的。那么我们假设两物体间第K个接触点Pk,该点的法向量是Nk,由 i 指向 j 。这时我们考虑物体 j 所受的力,首先有穿透产生的弹簧力,还应该有弹簧回复产生的阻尼力,那么,我们就可以得到 j 所受到的穿透力。

其中
![]()
表示相对速度。
又由于力的作用是相互的,那么

同样的道理我们可以求出穿透产生的力矩

rkj表示的是在 j 的质心坐标系中Pk的位置。
这样我们就可以计算出物体与物体接触所产生的力。然而事情没有那么简单。大部分情况下,我们很难得到令我们满意的接触法向量与穿透深度。比如

又或者一个平面上的正方体盒子

再或者,当某些时候接触法线变化会出现不连续的情况,就比如第一个问题图片那样。
第一个问题出现的原因是因为在计算的时候只考虑局部,当我们从全局出发就不需要考虑这个问题。
第二个问题,可以通过多个点采样来避免。
第三个问题,有另外特定的方法去解决。























 154
154

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








