堆排序-Head Sort

HANWEN KE

于 2022-08-31 17:50:25 发布

阅读量599

点赞数

分类专栏：数据结构与算法文章标签：算法数据结构排序算法

本文链接：https://blog.youkuaiyun.com/weixin_41694574/article/details/126628805

版权

本文介绍了堆排序算法的工作原理，包括如何构建初始堆、处理堆顶记录以及如何调整剩余记录形成新堆。堆排序是一种基于比较的排序算法，通过构建和调整二叉堆来实现排序。文中还给出了堆排序的C++实现代码，展示了如何将随机数数组进行排序。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

堆排序

堆的定义

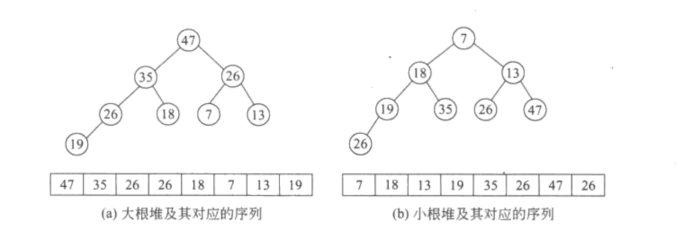
堆是具有下列性质的完全二叉树：每个结点的值都小于或等于其左右孩子终点的值（小根堆）或者每个结点的值都大于或等于左右结点孩子的值（大根堆）

堆排序要解决的关键问题

如何将一个无序的序列构造成一个堆（即初始建堆）
1. 无序序列建堆是一个反复筛选的过程。因此序列就是一颗完全二叉树的顺序存储，则所有的叶子结点也是堆，所以只需要从 最后一个分支结点开始执行筛选过程直到根节点
如何处理堆顶记录
初始建堆之后，将待排序序列分成无序区和有序区两个部分，其中无序区为堆，且包括全部待排序记录，有序区为空。将堆顶与堆中最后一个记录交换，则堆中减少了一个记录，有序区增加了一个记录。
如何调整剩余记录，成为一个新的堆（即重新建堆）
1. 第i趟排序后，无序区有n-i个记录，在无序区对应的完全二插树只需要筛选根结点即可重新建堆。

筛选思路

设置i和j分别指向当前要筛选的结点和要筛选结点的左孩子
若结点i已经是叶子，则筛选完毕，算法结束；否则执行下述操作
1. 将j指向结点i的左右孩子中的较大者
2. 如果r[i]>r[j],则筛选完毕，算法结束
3. 如果r[i]<r[j]，则将r[i]与r[j]交换，令i=j,转步骤二继续筛选

树以数组形式存储–其对应的下标关系

假设n为根结点：其左子树为2n,其右子树为 2n+1

堆排序

//
// Created by HANWENKE on 2022/8/31.
//
#include <iostream>
#include <vector>
using namespace std;
void Shift(vector<int>&nums,int len,int i){
   
    int index