聚类算法

目录：

• 什么是聚类、相似度的度量公式、聚类的思想
• 聚类的思想
• K-means聚类
• 聚类算法效果评估(准确率、召回率等)
• 层次聚类算法
• 密度聚类算法

一、什么是聚类及相似度的度量公式
（1）什么是聚类
聚类就是对大量未知标注的数据集，按照数据内部存在的数据特征将数据集划分 为多个不同的类别，使类别内的数据比较相似，类别之间的数据相似度比较小； 属于无监督学习 聚类算法的重点是计算样本项之间的相似度，有时候也称为样本间的距离。
和分类算法的区别
分类算法是有监督学习，基于有标注的历史数据进行算法模型构建 聚类算法是无监督学习，数据集中的数据是没有标注的
（2）距离的度量公式
闵可夫斯基距离(Minkowski)

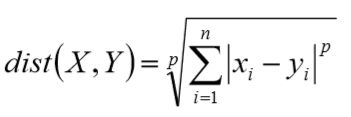
当p为1的时候是曼哈顿距离(Manhattan)， 当p为2的时候是欧式距离(Euclidean)， 当p为无穷大的时候是切比雪夫距离(Chebyshev)

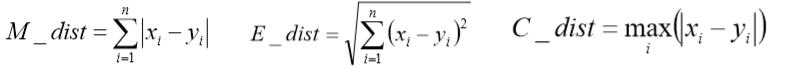
（3）聚类的思想
给定一个有M个对象的数据集，构建一个具有k个簇的模型，其中k<=M。满足 以下条件： 每个簇至少包含一个对象 每个对象属于且仅属于一个簇 将满足上述条件的k个簇成为一个合理的聚类划分
基本思想：对于给定的类别数目k，首先给定初始划分，通过迭代改变样本和簇 的隶属关系，使的每次处理后得到的划分方式比上一次的好(总的数据集之间的距离和变小了)
二、keans算法
1、kmeans算法的思想
K-means算法，也称为K-平均或者K-均值，是一种使用广泛的最基础的聚类算法，一般作为掌握聚类算法的第一个算法 。
假设输入样本为T=X1,X2,…,Xm;则算法步骤为（使用欧几里得距离公式）：

• 选择初始化的k个类别中心a1,a2,…ak;
• 对于每个样本Xi，将其标记位距离类别中心aj最近的类别j
• 更新每个类别的中心点aj为隶属该类别的所有样本的均值
• 重复上面两步操作，直到达到某个中止条件
  中止条件：
• 迭代次数、最小平方误差MSE、簇中心点变化率
  解析：
  ①我们先随机的选择其中的k个点为中心
  ②对于其余的所有点都算一个距离这k个点的距离，比如我们有m个点，那么从1-m开始算起，先算第一个点到这k个点的距离，选择最小的距离并标记其为第j个类，经过一次全部样本的扫描，这m个样本分成了k类
  ③将每组分成的样本都计算一次均值，并将均值作为新的质心
  ④不断重复②③这两步的步骤，直到达到终止条件
  终止条件：
• 迭代次数：比如一开始限制迭代多少次（20、30）
• 最小平方误差（MSE):算出所有一个类中所有点距离簇心的欧式距离之和，然后把这k个点的欧式距离之和（最小平方误差）相加，当其小于给定的最小平方误差和时终止迭代。
  
• 簇中心变化率：我们每次进行均值计算时都要更新一次簇心，那么更新簇心时都和前一个簇心比较一次两者的变化率，即移动了多少，如果小于某个值则停止迭代。

2、kmeans算法的优缺点
缺点：
①K-means算法在迭代的过程中使用所有点的均值作为新的质点(中心点)，如果簇 中存在异常点，将导致均值偏差比较严重 ，即kmeans算法对异常点是比较敏感的。
② K-means算法是初值敏感的，选择不同的初始值可能导致不同的簇划分规则。即kmeans算法对初始值的选择特别敏感
③K值是用户给定的，在进行数据处理前，K值是未知的，不同的K值得到的结果也不一样
优点：
①理解容易，聚类效果不错
②处理大数据集的时候，该算法可以保证较好的伸缩性和高效率
3、kmeans算法代码

###生成随机的质心
def randcent(dataset,k):
    mat(dataset)
    ##数据级有多少列
    n=shape(dataset)[1]
    ##生成K行，n列的0矩阵
    centroids=mat(zeros((k,n)))
    for j in range(n):
        minj=min(dataset[:,j])
        rangej=float(max(dataset[:,j])-minj)
        centroids[:,j]=minj+rangej*random.rand(k,1)
    return centroids
##计算距离
def disteclud(A,B):
    return sqrt(sum(power(A-B,2)))
##k_means算法,三个参数数据集,距离计算公式，初始质心的选择
##返回这个n个样本分类的矩阵
def kmeans(k,dataset,distmethod=disteclud,createcent=randcent):
    k=int(k)
    dataset=dataset
    m=shape(dataset)[0]
    clusterassment=mat(zeros((m,2)))
    centers=createcent(dataset,k)
    clusterchanged=True
    while clusterchanged:
        clusterchanged=False
        for i in range(m):
            mindist=inf;minindex=-1
            for j in range(k):
                distji=distmethod(centers[j,:],dataset[i,:])
                if distji<mindist:
                    mindist=distji;minindex=j
            if clusterassment[i,0] != minindex:
                clusterchanged = True
                clusterassment[i,:]=minindex,mindist**2
        for cent in range(k):
            ptsincluster=dataset[nonzero(clusterassment[:,0].A==1)[0]]     
            centers[1,:]=mean(ptsincluster,axis=0)
    return clusterassment,centers        

3.2 k-means算法中k值怎么选择
在进行k-means的k值选择时一定要明白如何进行判断k值选择的好坏，即聚类完成后的效果怎么判断。常见的方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。个人比较喜欢Calinski-Harabasz Index，这个计算简单直接，得到的Calinski-Harabasz分数值s越大则聚类效果越好。　①Calinski-Harabasz分数值s的数学计算公式是：

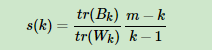
其中m为训练集样本数，k为类别数。Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵。tr为矩阵的迹。协方差矩阵的迹是方差和，这里即类别内部数据的方差和越小越好，类别之间的方差和越大越好
即这里要计算组内方差和和组间方差和。
补充1：
组内平方和和组间平方和计算公式

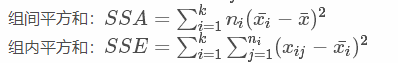
协方差矩阵计算公式：


②轮廓系数
计算 a(i) = average(i向量到所有它属于的簇中其它点的距离)
计算 b(i) = min (i向量到其他簇内的所有点的平均距离)（距离这个点最近的簇距离的最小值）
那么 i 向量轮廓系数就为：

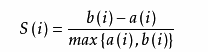
可见轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优。
将所有点的轮廓系数求平均，就是该聚类结果总的轮廓系数。

from sklearn.metrics import silhouette_score

python sklearn中有计算轮廓系数的包。
3、二分k-means算法
解决K-Means算法对初始簇心比较敏感的问题，二分K-Means算法是一种弱化初始质心 的一种算法，具体思路步骤如下：
①将所有样本数据作为一个簇放到一个队列中
②从队列中选择一个簇进行K-means算法划分，划分为两个子簇，并将子簇添加到队列中
③循环迭代第二步操作，直到中止条件达到(聚簇数量、最小平方误差、迭代次数等)
④队列中的簇就是最终的分类簇集合
从队列中选择划分聚簇的规则一般有两种方式，分别如下：
①对所有簇计算误差和SSE(SSE也可以认为是距离函数的一种变种)，选择SSE最大的聚簇进行划分 操作(优选这种策略) 。
②选择样本数据量最多的簇进行划分操作

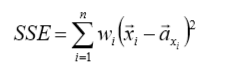
这个公式代表计算每个簇中样本距离簇心的距离平方和，wi为第i个样本的权重，我们可以设置为1，然后选出SSE最大的簇进行划分。
（注：由于我们是一个质心一个质心选择出的k个质心，所以不会出现质心之间的过近的情况，这就保证了初始质心敏感的问题）

4、K-Means++算法
解决K-Means算法对初始簇心比较敏感的问题，K-Means++算法和K-Means算 法的区别主要在于初始的K个中心点的选择方面，K-Means算法使用随机给定的 方式，K-Means++算法采用下列步骤给定K个初始质点：
①从数据集中任选一个节点作为第一个聚类中心
②对数据集中的每个点x，计算x到所有已有聚类中心点的距离和D(X)，基于D(X)最大选择出下一个聚类中心点(距离较远的一个点成为新增的一个聚类中心点)
③重复步骤2直到找到k个聚类中心点
缺点：由于聚类中心点选择过程中的内在有序性，在扩展方面存在着性能方面的 问题(第k个聚类中心点的选择依赖前k-1个聚类中心点的值)。
三、层次聚类
层次聚类方法对给定的数据集进行层次的分解，直到满足某种条件为止，传统的 层次聚类算法主要分为两大类算法：
凝聚的层次聚类：
AGNES算法(AGglomerative NESting):采用自底向上的策略。最初将每个对象作为一个簇，然后这些簇根据某些准则被一步一步合并，两个簇间的距离可以由这两个不同簇中距离最近的数据点的相似度来确定；聚类的合并过程反复进行直到所 有的对象满足簇数目。
分裂的层次聚类：
DIANA算法(DIvisive ANALysis)：采用自顶向下的策略。首先将所 有对象置于一个簇中，然后按照某种既定的规则逐渐细分为越来越小的簇(比如最大的欧式距离)，直到达到某个终结条件(簇数目或者簇距离达到阈值)。
2、AGNES和DIANA算法优缺点

四、密度聚类算法-DBSCAN算法
一个比较有代表性的基于密度的聚类算法，相比于基于划分的聚类方法和层次聚类方法，DBSCAN算法将簇定义为密度相连的点的最大集合，能够将足够高密度的区域划分为簇，并且在具有噪声的空间数据商能够发现任意形状的簇。
DBSCAN算法的核心思想是：用一个点的ε邻域内的邻居点数衡量该点所在空间 的密度，该算法可以找出形状不规则的cluster，而且聚类的时候事先不需要给定cluster的数量
DBSCAN算法基本概念1

DBSCAN算法常见概念2

DBSCAN算法基本概念3

DBSCAN算法基本概念4

DBSCAN密度聚类算法最重要的几个参数分别是
①距离的度量方式：采用什么距离来计算点与点之间的距离
②领域，在哪个半径之内点是密度可达的
③Minpts,密度可达半径中拥有的最少样本数目

DBSCAN对异常值点也很敏感

2、代码实现

# visitlist类用于记录访问列表
# unvisitedlist记录未访问过的点
# visitedlist记录已访问过的点
# unvisitednum记录访问过的点数量
class visitlist:
    def _init_(self, count=0):
        self.unvisitedlist=[i for i in range(count)]
        self.visitedlist=list()
        self.unvisitednum=count

    def visit(self, pointId):
        self.visitedlist.append(pointId)
        self.unvisitedlist.remove(pointId)
        self.unvisitednum -= 1

import numpy as np
import matplotlib.pyplot as plt
import math
import random

def  dist(a, b):
    # 计算a,b两个元组的欧几里得距离
    return math.sqrt(np.power(a-b, 2).sum())
#函数最终返回分类的结果列表
def my_dbscanl(dataSet, eps, minPts):
    # numpy.ndarray的 shape属性表示矩阵的行数与列数
    nPoints = dataSet.shape[0]
    # (1)标记所有对象为unvisited
    # 在这里用一个类vPoints进行买现
    vPoints = visitlist(count=nPoints)
    # 初始化簇标记列表C,簇标记为 k
    k = -1
    C = [-1 for i in range(nPoints)]
    while(vPoints.unvisitednum > 0):
        # (3)随机上选择一个unvisited对象p
        P = random.choice(vPoints.unvisitedlist)
        # (4)标记p为visited
        vPoints.visit(p)
        # (5)if p的$\varepsilon$-邻域至少有MinPts个对象
        # N是p的$\varepsilon$-邻域点列表
        N = [i for i in range(nPoints) if dist(dataSet[i], dataSet[p])<= eps]
        if  len(N) >= minPts:
            # (6)创建个新簇C，并把p添加到C
            # 这里的C是一个标记列表，直接对第p个结点进行赋植
            k += 1
            C[p]=k
            # (7)令N为p的ε-邻域中的对象的集合
            # N是p的$\varepsilon$-邻域点集合
            # (8) for N中的每个点p'
            for p1 in N:
                # (9) if p'是unvisited
                if p1 in vPoints.unvisitedlist:
                    # (10)标记p’为visited
                    vPoints.visit(p1)
                    # (11) if p'的$\varepsilon$-邻域至少有MinPts个点，把这些点添加到N
                    # 找出p'的$\varepsilon$-邻域点，并将这些点去重添加到N
                    M=[i for i in range(nPoints) if dist(dataSet[i], \
                        dataSet[p1]) <= eps]
                    if len(M) >= minPts:
                        for i in M:
                            if i not in N:
                                N.append(i)
                    # (12) if p'还不是任何簇的成员，把P'添加到C
                    # C是标记列表，直接把p'分到对应的簇里即可
                    if  C[p1] == -1:
                        C[p1]= k
        # (15)else标记p为噪声
        else:
            C[p]=-1

    # (16)until没有标t己为unvisitedl内对象
    return C

###测试数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X1, Y1 = datasets.make_circles(n_samples=2000, factor=0.6, noise=0.05,
                               random_state=1)
X2, Y2 = datasets.make_blobs(n_samples=500, n_features=2, centers=[[1.5,1.5]],
                             cluster_std=[[0.1]], random_state=5)

X = np.concatenate((X1, X2))
plt.figure(figsize=(12, 9), dpi=80)
plt.scatter(X[:,0], X[:,1], marker='.')
plt.show()    

聚类前

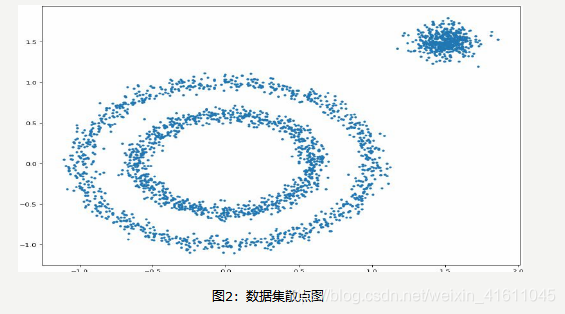
聚类后：

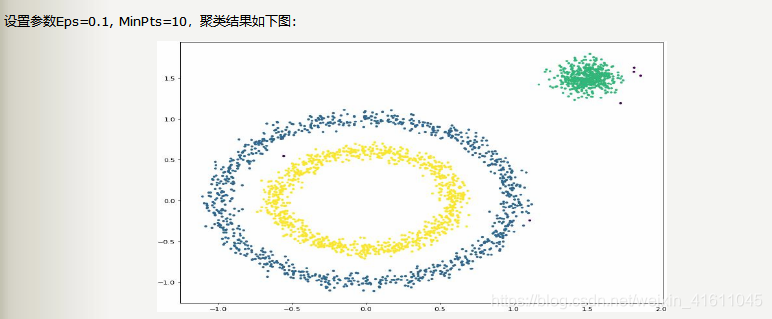
（注：当扫描结果太慢时，我们可以采用KD-Tree进行优化）