一.实现“与”运算
1.采用单极点二值函数时:
将以下程序直接粘贴到Matlab的m文件中,便可直接运行,得到结果。(已亲自尝试,确实可以直接得到结果)
function Perception1_1_Yu_DanJiDianFunc()
close all %关闭所有figure
rand('state',sum(100*clock)) %随机数种子用时钟进行初始化
P=4;%训练样本数
%输入训练样本:
X(:,1)=[0;0];
X(:,2)=[0;1];
X(:,3)=[1;0];
X(:,4)=[1;1];
X=[-1*ones(1,4); X];%考虑阈值,设x0=-1
%输入对应期望输出:
d=[0, 0, 0, 1];
%设置感知器参数
InDim=2; %输入样本维数
OutDim=1; %输出维数
MaxTrainNumber=10;%最大训练次数
Eta=0.1;%学习率
%感知器训练
%权值初始化
W=rand(InDim,OutDim);
%设置阈值
T=0.1;
WExpand=[T; W];%合并阈值到权值
w1=[]; %创建w1矩阵
w2=[]; %创建w2矩阵
ErrHistory=[];
for i=1:MaxTrainNumber %循环MaxTrainNumber次
for p=1:P
net(p)=WExpand'*X(:,p);%计算样本p的net值
o(p)=SinPoleTwoValue_f(net(p));%调用编辑好的变换函数,得到输出值
Err(p)=o(p)-d(p);%计算误差
WExpand=WExpand+Eta*(d(p)-o(p))*X(:,p);%根据误差更新权值
end
%计算总误差
Err_sum=sum(abs(Err));
%写出权值w1,w2的一维矩阵复合
w1=[w1 WExpand(2)];
w2=[w2 WExpand(3)];
%记录每次权值调整后的训练误差
ErrHistory=[ErrHistory Err_sum];
if Err_sum==0, break, end %判断训练是否停止
end
W=WExpand(2:3);
T=WExpand(1);
disp(['The final Error is: ',num2str(Err_sum) ,'.']);
disp(['The curren Epoch is: ',num2str(i) ,'.']);
disp('The Final W is: ');
disp(num2str(W))
disp(['The Final T is: ',num2str(T) ,'.']);
%验证
O=SinPoleTwoValue_f(WExpand'*X);
True_Chart=[X(2:3,:)',O'];
disp('The Result is:')
disp('x1 x2 y')
disp(num2str(True_Chart));
% %画误差收敛曲线
% figure;
% hold on
% grid on
[xx,NumOfErrReachZero]=size(ErrHistory)
% plot(1:NumOfErrReachZero,ErrHistory,'r--');
% title('感知器的收敛曲线')
%画权值w1变化曲线
figure
hold on
grid on
plot(w1,'r-')
xlabel('迭代次数')
ylabel('w1')
title('权值w1的变化过程')
%画权值w2变化曲线
figure
hold on
grid on
plot(w2,'r-')
xlabel('迭代次数')
ylabel('w2')
title('权值w2的变化过程')
%
% %画出输入样本的分布
% figure;%画图
% hold on
% grid on
% for p=1:P
% if d(p)==0 %如果输出为0
% XXX=X(2,p);
% YYY=X(3,p);
% plot(X(2,p),X(3,p),'k*')
% else %否则
% ZZZ=X(2,p);
% QQQ=X(3,p);
% plot(X(2,p),X(3,p),'ro')
% end
% end
% %画出分界线w1x1+w2x2-T=0
% x1=-1:1:2;
% x2=(T-W(1).*x1)./W(2);
% plot(x1,x2,'b--');
% axis([-1 2 -1 2]);
% xlabel('Inputx')
% ylabel('Outputy')
% title('感知器处理与问题结果')
function f=SinPoleTwoValue_f(x) %定义变换函数
f=(x>=0); %如果x>=0,则f=1,否则f=0.
下附运行结果截图

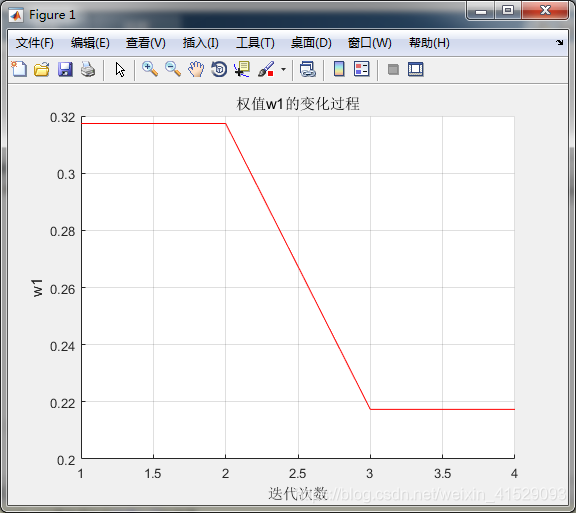
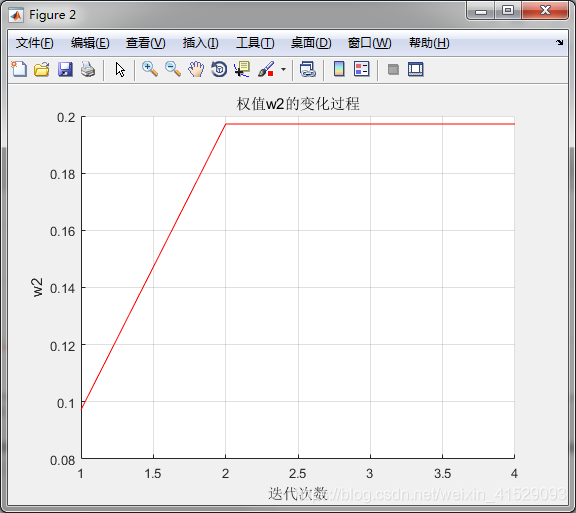
2.采用Sigmoid函数时
再将以下程序直接粘贴到Matlab的m文件中,便可直接运行,得到结果。(已亲自尝试,确实可以直接得到结果)
function Perception1_2_Yu_SigmoidFunc()
close all %关闭所有figure
rand('state',sum(100*clock)) %随机数种子用时钟进行初始化
P=4;%训练样本数
%输入训练样本:
X(:,1)=[0;0];
X(:,2)=[0;1];
X(:,3)=[1;0];
X(:,4)=[1;1];
X=[-1*ones(1,4); X];%考虑阈值,设x0=-1
%输入对应期望输出:
d=[0, 0, 0, 1];
%设置感知器参数
InDim=2; %输入样本维数
OutDim=1; %输出维数
MaxTrainNumber=10;%最大训练次数
Eta=10;%学习率
%感知器训练
%权值初始化
W=rand(InDim,OutDim);
%设置阈值
T=0.1;
WExpand=[T; W];%合并阈值到权值
w1=[]; %创建w1矩阵
w2=[]; %创建w2矩阵
ErrHistory=[];
for i=1:MaxTrainNumber %循环MaxTrainNumber次
for p=1:P
net(p)=WExpand'*X(:,p);%计算样本p的net值
o(p)=sigmoid(net(p));%调用编辑好的变换函数,得到输出值
Err(p)=o(p)-d(p);%计算误差
WExpand=WExpand+Eta*(d(p)-o(p))*X(:,p);%根据误差更新权值
end
%计算总误差
Err_sum=sum(abs(Err));
%写出权值w1,w2的一维矩阵复合
w1=[w1 WExpand(2)];
w2=[w2 WExpand(3)];
%记录每次权值调整后的训练误差
ErrHistory=[ErrHistory Err_sum];
if Err_sum==0, break, end %判断训练是否停止
end
W=WExpand(2:3);
T=WExpand(1);
disp(['The final Error is: ',num2str(Err_sum) ,'.']);
disp(['The curren Epoch is: ',num2str(i) ,'.']);
disp('The Final W is: ');
disp(num2str(W))
disp(['The Final T is: ',num2str(T) ,'.']);
%验证
O=sigmoid(WExpand'*X);
True_Chart=[X(2:3,:)',O'];
disp('The Result is:')
disp('x1 x2 y')
disp(num2str(True_Chart));
% %画误差收敛曲线
% figure;
% hold on
% grid on
[xx,NumOfErrReachZero]=size(ErrHistory)
% plot(1:NumOfErrReachZero,ErrHistory,'r--');
% title('感知器的收敛曲线')
%
%画权值w1变化曲线
figure
hold on
grid on
plot(w1,'r-')
xlabel('迭代次数')
ylabel('w1')
title('权值w1的变化过程')
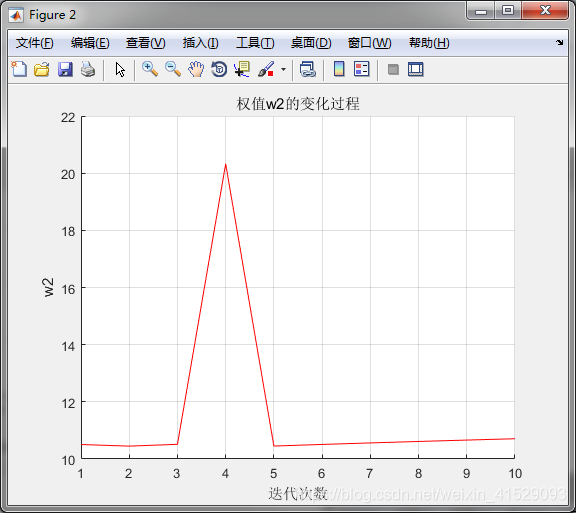
%画权值w2变化曲线
figure
hold on
grid on
plot(w2,'r-')
xlabel('迭代次数')
ylabel('w2')
title('权值w2的变化过程')
% %画出输入样本的分布
% figure;%画图
% hold on
% grid on
% for p=1:P
% if d(p)==0 %如果输出为0
% XXX=X(2,p);
% YYY=X(3,p);
% plot(X(2,p),X(3,p),'k*')
% else %否则
% ZZZ=X(2,p);
% QQQ=X(3,p);
% plot(X(2,p),X(3,p),'ro')
% end
% end
% %画出分界线w1x1+w2x2-T=0
% x1=-1:1:2;
% x2=(T-W(1).*x1)./W(2);
% plot(x1,x2,'b--');
% axis([-1 2 -1 2]);
% xlabel('Inputx')
% ylabel('Outputy')
% title('感知器处理与问题结果')
function output = sigmoid(x)
output=1./(1+exp(-x));
下附运行结果截图
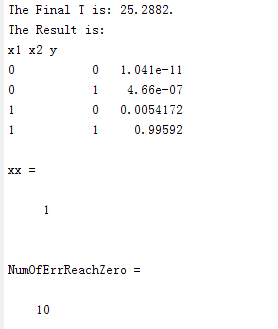
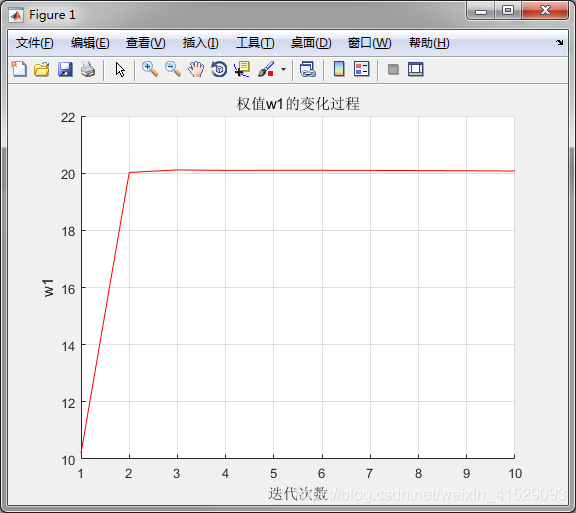








 本文通过使用Matlab编程,详细介绍了如何实现感知器来完成逻辑与运算。包括采用单极点二值函数和Sigmoid函数两种方式,展示了完整的代码实现及运行结果。文章深入解析了感知器训练过程中的权值更新、误差计算等关键步骤。
本文通过使用Matlab编程,详细介绍了如何实现感知器来完成逻辑与运算。包括采用单极点二值函数和Sigmoid函数两种方式,展示了完整的代码实现及运行结果。文章深入解析了感知器训练过程中的权值更新、误差计算等关键步骤。
















 3735
3735

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








