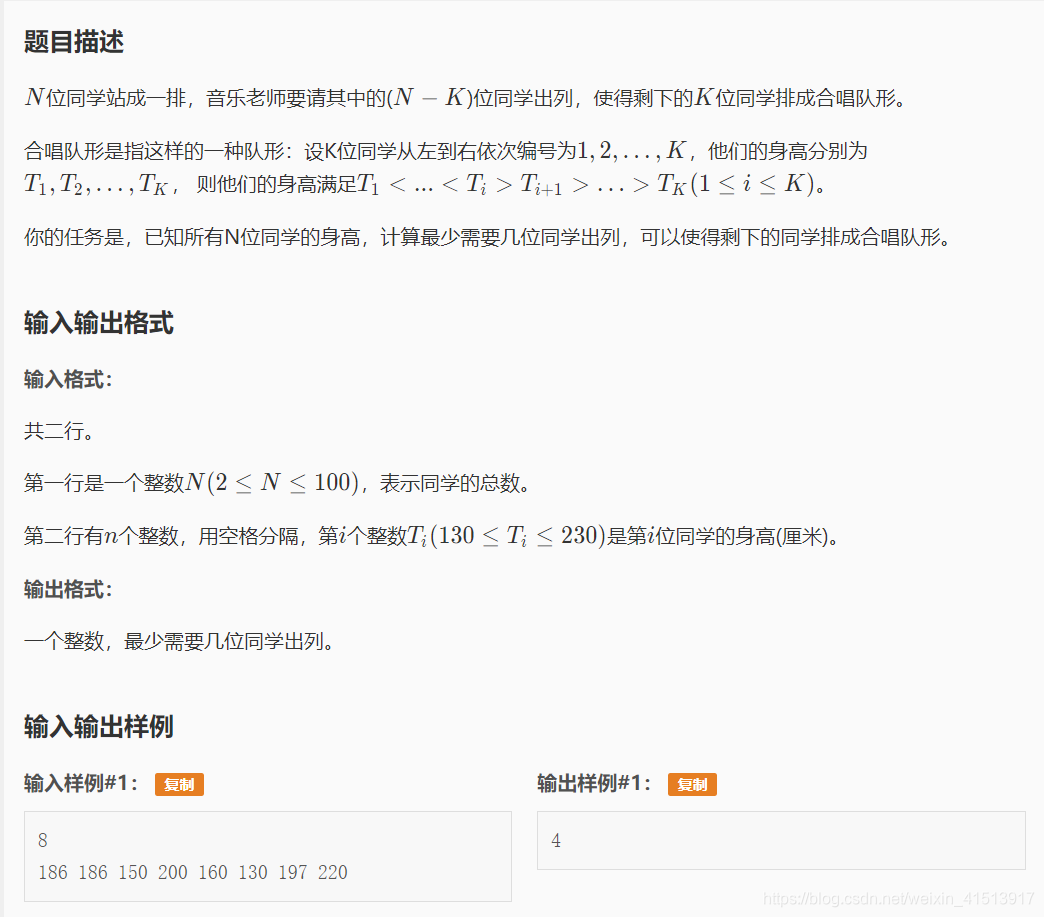
P1091 合唱队形（最长上升子序列）_编程题合唱队+最长上升子序列-优快云博客

本文深入探讨了求解最长上升子序列问题的算法思路，通过动态规划方法，分别从前向后和从后向前计算子序列长度，最终找出最长可能的序列长度，为理解复杂序列分析提供了清晰的路径。

题目

分析

求最长上升子序列的题目。

对于第 $i$ 个点，如果知道以 $i$ 结尾最长的上升子序列长度，和，以 $i$ 开头的最长上升子序列长度。遍历所有的 $i$ ，最大值对应的是队列的最长可能。用学生数量 - 队列长度 +1 可得答案。

有个弯没绕过来，就是，以 $i$ 开头的最长上升子序列长度，，其实可以看做，，从数组尾部 n -- > 1 的以 $i$ 结尾的最长子序列长度。

代码


//P1091 
#include<iostream>
#include<algorithm>
#include<set>
#include<cstring>
#include<queue>
#include<stack>
#include<vector>
#include<stdio.h>
using namespace std;
#define ll long long

int num[105];
int dp[105];
int dp2[105];

int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&num[i]);
		
	for(int i=1;i<=n;i++)
	{
		dp[i]=1;
		dp2[i]=1;
	}
	
	//dp[i] 以i结尾的，最长上升序列长度
	//1-n
	for(int i=2;i<=n;i++)
	{
		for(int j=1;j<i;j++)
		{
			if(num[j]<num[i])
				dp[i]=max(dp[i],dp[j]+1);
		}
	}
	
//	for(int i=1;i<=n;i++)
//		cout<<dp[i]<<" ";
//		cout<<endl;
		
	//dp2[i] 以i开头的，最长上升列的长度
	// n->1
	for(int i=n-1;i>=1;i--)
	{
		for(int j=n;j>i;j--)
		{
			if(num[j]<num[i])
				dp2[i]=max(dp2[i],dp2[j]+1);
		}
	 } 
		
//	for(int i=1;i<=n;i++)
//		cout<<dp2[i]<<" ";
//	cout<<endl;
	
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		ans=max(ans,dp[i]+dp2[i]);
	}
	cout<<n-ans+1<<endl;
}