C++选择排序之直接选择排序、堆排序

直接选择排序
基本思想：不断从待排序的数据中选择数值小的（或大的）数据，依次排入到已排好序的序列后面。
算法： 设 r [1,2,…n];

1.第一趟扫描选出n个数据中最小的元素，并与 r [1]交换位置；
2. 第二趟扫描余下的 n-1 个数据中最小的，并与 r [2]交换位置；
3. 以此类推，直到第 n-1 趟扫描结束，所有数据有序为止。

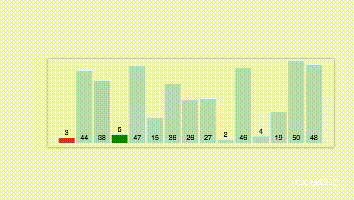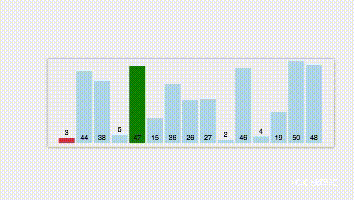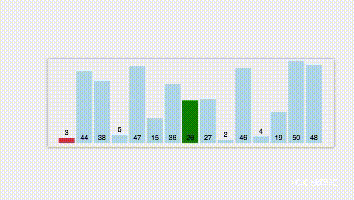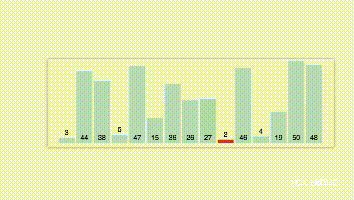
for(int i=0;i<n;i++)
		for(int j=i+1;j<n;j++)//�ص�
			if(a[i]>a[j]){
				int temp=a[i];
				a[i]=a[j];
				a[j]=temp;}	
		for(int i=0;i<n;i++)
		cout<<a[i]  <<endl;	
        system("pause");
	    return 0;

排序效率：
时间复杂度：O(n²)
空间复杂度：O(1)

堆排序：
为了避免直接排序中复杂重复比较的缺点，引入了树形选择排序方法——堆排序。
基本思想：将序列中的元素看成一个完全二叉树的存储结构，
该堆的实质满足如下性质的完全二叉树：
树中的任意非叶子结点的数据 **均不大于（或不小于）**其左右孩子（若存在）结点的数据。
算法：

1. 将n个元素建成堆，将堆顶元素输出，得到n个元素中最大（最小的）元素。
2. 将剩下的 n-1 个元素建成堆，输出堆顶元素，得到n个元素中次小的元素。
3. 实现堆排序需解决的问题：
   ①构建堆；②调整堆。
   

void swap(int arr[], int i,int j){
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}
void heapify(int tree[], int n,int i)//n为总数据数
{
	if( i > n )  return;
	int c1 = 2 * i+1;//子类
	int c2 = 2 * i+2;
	int max = i;//父类
	if(c1 < n && tree[c1] >tree[max]){
		max = c1;
	}
	if(c2 < n && tree[c2] > tree[max]){
		max = c2;
	}
	if(max != i){
		swap(tree, max, i);
		heapify(tree, n, max);//递归函数
	}
}

void bulid_heap(int tree[], int n){//建立堆，所有父节点 > 子节点
	int last_node = n - 1;
	int parent = (last_node - 1) / 2;
	int i;
	for(i = parent; i >=0; i--){
		heapify(tree, n, i);
	}
}

void heap_sort(int tree[],int n){//堆排序
	bulid_heap(tree, n);
	int i;
	for(i = n-1; i >= 0; i--){
		swap(tree, i, 0);
		heapify(tree, i, 0);
	}
}

排序效率：
时间复杂度：O(nlog₂n)
空间复杂度：O(1)