CGL_1_B: Reflection（几何）

最新推荐文章于 2024-07-29 23:52:08 发布

creator平

最新推荐文章于 2024-07-29 23:52:08 发布

阅读量435

点赞数

CC 4.0 BY-SA版权

分类专栏：数学几何

本文链接：https://blog.youkuaiyun.com/weixin_41380961/article/details/99416972

数学几何专栏收录该内容

11 篇文章

订阅专栏

本文详细介绍了一个几何算法，用于计算平面中一点关于另一条线段的反射点。通过给出的输入和输出样例，展示了如何使用复数进行计算，提供了一个完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Reflection

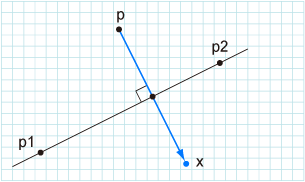
For given three points p1, p2, p, find the reflection point x of p onto p1p2.

Input

xp1 yp1 xp2 yp2
q
xp0 yp0
xp1 yp1
...
xpq−1 ypq−1

In the first line, integer coordinates of p1 and p2 are given. Then, q queries are given for integer coordinates of p.

Output

For each query, print the coordinate of the reflection point x. The output values should be in a decimal fraction with an error less than 0.00000001.

Constraints

1 ≤ q ≤ 1000
-10000 ≤ xi, yi ≤ 10000
p1 and p2 are not identical.

Sample Input 1

Sample Output 1

-1.0000000000 -1.0000000000
0.0000000000 -1.0000000000
1.0000000000 -1.0000000000

Sample Input 2

Sample Output 2

4.2400000000 3.3200000000
3.5600000000 2.0800000000
2.8800000000 0.8400000000

题目连接：http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=CGL_1_B

#include<string.h>
#include<algorithm>
#include<stdio.h>
#include<complex>
using namespace std;
typedef complex<double> qua;
qua solve(qua a,qua b,qua c)
{
    b=b-a,c=c-a;
    return a+b*conj(c/b);
}
int main()
{
    int m;
    double x1,y1,x2,y2,x3,y3;
    scanf("%lf%lf%lf%lf%d",&x1,&y1,&x2,&y2,&m);
    while(m--)
    {
        scanf("%lf%lf",&x3,&y3);
        qua ans=solve(qua(x1,y1),qua(x2,y2),qua(x3,y3));
        printf("%.8f %.8f\n",ans.real(),ans.imag());
        qua b =qua(x2,y2);
    }
}