常见排序算法

插入排序

插入排序是一个数据向已经有序的数组中插入数据。见下图

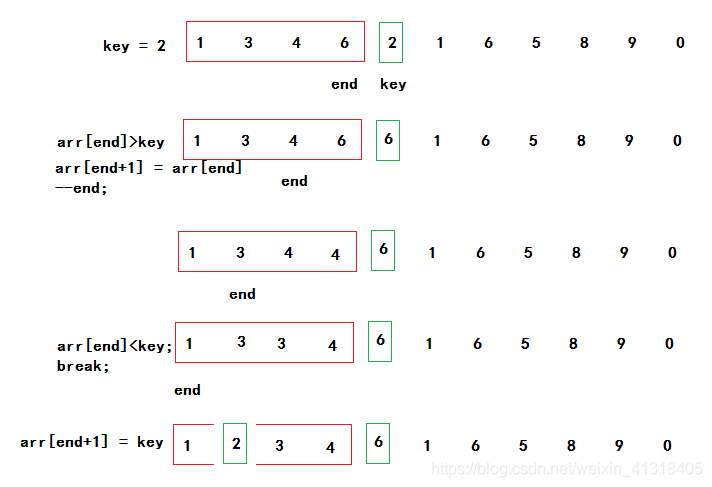
插入排序时间复杂度：稳定的，最好情况是接近有序O(N)，最坏情况下是逆序O(N^2)，平均O(N^2)。优化：可以采用二分查找查找元素应该插入的位置。 

//插入排序
//最好O(N)
//最坏O(N^2)
//可以采用二分查找
void InsertSort(std::vector<int> &v)
{
  int end = 0;
  for(size_t i = 0;i<v.size();++i)
  {
    end = i-1;
    int key = v[i];
    while(end>=0)
    {
      if(key<v[end])
      {
        v[end+1] = v[end];
        --end;
      }
      else 
        break;
    }
    v[end+1] = key;
  }
}

希尔排序

希尔排序其实根据直接插入排序的优缺点来设计的。直接插入排序主要适用于排接近有序的数据，所以希尔排序利用这一点设计包含两部分：（1）预排序（2）直接插入排序

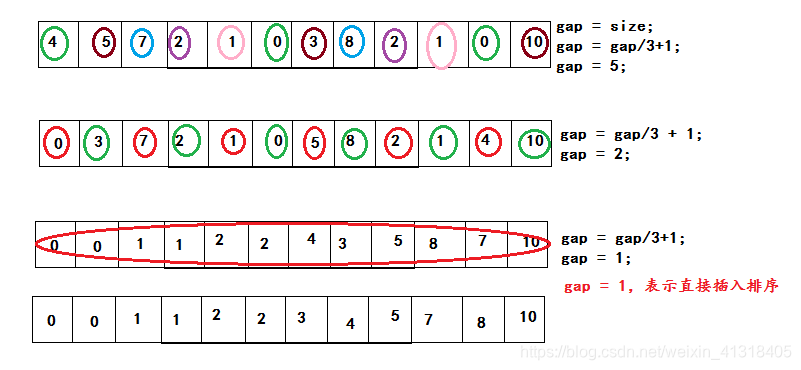
预排序：希尔排序是取间隔排序，间隔gap = size，gap = gap/3+1；间隔越大，排的越快。间隔越小，效率越高。

直接插入排序：当gap = 1时，其实就是接近有序的数据进行直接插入排序。

void ShellSort(std::vector<int> &v)
{
  size_t gap = v.size();
  while(gap != 1)
  {
    gap = gap/3 + 1;
    for(size_t i = gap;i<v.size();i = i+gap)
    {
      int key = v[i];
      int end = i-gap;
      while(end>=0)
      {
        if(v[end]>key)
        {
          v[end+gap] = v[end];
          end = end-gap;
        }
        else 
          break;
      }
      v[end+gap] = key;
    }
  }
}

希尔排序：是不稳定的，因为不能保证同样的数据分配到同一组，所以不稳定。

时间复杂度：最好O(N)，平均O(N^1.2~N^1.3)，最坏O(N^2)；

选择排序

选择排序：每次从序列中选出最大或者最小的数据，交换到最后。

//一次排一个
void SelectSort(std::vector<int> &v)
{
  size_t end = v.size()-1;

  while(end != 0)
  {
    size_t max = 0;
    for(size_t i = 0;i<=end;++i)
    {
      if(v[max]<v[i])
        max = i;
    }
    if(max != end)
    {
      size_t tmp = v[max];
      v[max] = v[end];
      v[end] = tmp;
    }
    --end;
  }
}

void Swap(int &left,int &right)
{
  int tmp = left;
  left = right;
  right = tmp;
}
//一次排两个
void SelectTwoSort(std::vector<int> &v)
{
  int begin = 0;
  int end = v.size()-1;
  while(begin<end)
  {
    int minPos = begin;
    int maxPos = begin;
    for(int i = begin;i<=end;++i)
    {
      if(v[minPos]>v[i])
        minPos = i;
      if(v[maxPos]<v[i])
        maxPos = i;
    }
    if(begin != minPos)
    {
      if(maxPos == begin)
        maxPos = minPos;
      Swap(v[begin],v[minPos]);
    }
    if(end != maxPos)
      Swap(v[end],v[maxPos]);
    --end;++begin;
  }
}

选择排序：不稳定，时间复杂度O(N^2)

堆排序

升序：大堆；降序：小堆；（1）建堆，从最后一个非叶子节点开始向下调整（2）交换堆顶节点和最后一个节点，然后向下调整堆顶节点（除去最后一个节点）。

void AdjustDown(std::vector<int> &v,int index,int root)
{
  size_t leftChild = (root<<1)+1;
  while(leftChild<(v.size()-index-1))
  {
    size_t rightChild = leftChild+1;
    int maxChild = leftChild;
    if(rightChild<(v.size()-index-1) && v[maxChild]<v[rightChild])
      maxChild = rightChild;
    if(v[root]<v[maxChild])
      Swap(v[root],v[maxChild]);
    else 
      break;
    root = maxChild;
    leftChild = (root<<1)+1;
  }
}
void CreateHeap(std::vector<int> &v,int parent)
{
  AdjustDown(v,0,parent);
}
void HeapSort(std::vector<int> &v)
{
  for(int i = (v.size()-2)>>1;i>=0;--i)
    CreateHeap(v,i);
  for(size_t i = 0;i<v.size();++i)
  {
    Swap(v[0],v[v.size()-1-i]);
    AdjustDown(v,i,0);
  }
}

时间复杂度：NlgN，不稳定

冒泡排序

从数组头部开始，不断比较相邻的两个元素的大小，让较大的元素逐渐往后移动（交换两个元素的值），直到数组的末尾。经过第一轮的比较，就可以找到最大的元素，并将它移动到最后一个位置。

第一轮结束后，继续第二轮。仍然从数组头部开始比较，让较大的元素逐渐往后移动，直到数组的倒数第二个元素为止。经过第二轮的比较，就可以找到次大的元素，并将它放到倒数第二个位置。

以此类推，进行 n-1（n 为数组长度）轮“冒泡”后，就可以将所有的元素都排列好。

void BubbleSort(std::vector<int> &v)
{
  for(size_t i = 0;i<v.size();++i)
  {
    bool flag = false;
    for(size_t j = 0;j<v.size()-1-i;++j)
    {
      if(v[j]>v[j+1])
      {
        Swap(v[j],v[j+1]);
        flag = true;
      }
    }
    if(flag == false)
      break;
  }
}

时间复杂度：最好O(N)，平均O(N^2)，最坏O(N^2)，不稳定·

快速排序

快排基本思想：分治算法

（1）取一个基准值；一般取最左边或者最右边的一个数

（2）根据基准值划分数据集合；左边的数据比基准值小，右边的数据比基准值大（升序）

（3）终止条件：快排小区间剩下一个数据或者没有数据

快速排序：最好和平均复杂度是O(NlgN)，递归空间复杂度O(lgN)，是一颗二叉树；最坏情况是有序或者接近有序或者基准值取得不合适，时间复杂度为O(N^2)，空间复杂度是O(N)退化为单支树。不稳定。

基准值取得不合适，容易造成单支树，所以可以采用三数取中方法。

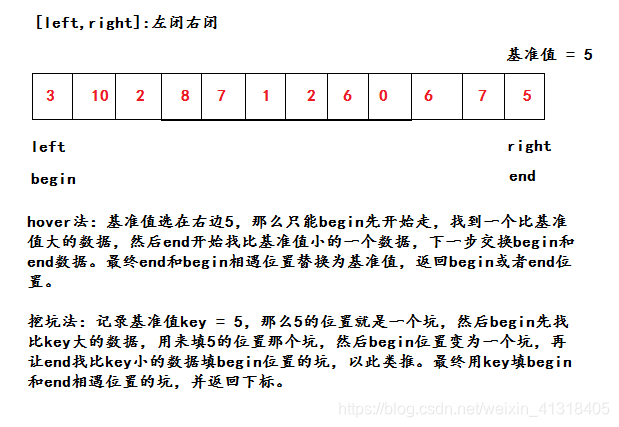
1. hover法
2. 挖坑法
3. 前后指针法

int Partition_1(std::vector<int> &v,int left,int right)
{
  int begin = left;//此处不是0
  int end = right;
  while(begin<end)
  {
    //基准值选右边，begin开始走
    //这里是小于等于，不能为小于
    while(begin<end && v[begin]<=v[right])
      ++begin;
    while(begin<end && v[end]>=v[right])
      --end;

    if(begin<end)
      Swap(v[begin],v[end]);
  }
  Swap(v[begin],v[right]);
  return begin;
}
int Partition_2(std::vector<int> &v,int left,int right)
{
  int begin = left;
  int end = right;
  int key = v[right];
  while(begin<end)
  {
    while(begin<end && v[begin]<=key)
      ++begin;
    v[end] = v[begin];
    while(begin<end && v[end]>=key)
      --end;
    v[begin] = v[end];
  }
  v[begin] = key;
  return begin;
}

//挖坑法
void _QuickSort(std::vector<int> &v,int left,int right)
{
  if(left>=right)//剩一个数据或者没有退出
    return;

  int div = Partition_1(v,left,right);//基准值位置

  _QuickSort(v,left,div-1);//左闭右闭
  _QuickSort(v,div+1,right);
}

void QuickSort(std::vector<int> &v)
{
  _QuickSort(v,0,v.size()-1);
}

int Partition_3(std::vector<int> &v,int left,int right)
{
  int div = left;
  int cur = left;

  while(cur != right)
  {
    while(cur != right && v[cur]>=v[right])
      ++cur;
    if(cur != right){
      Swap(v[div],v[cur]);
      ++div;++cur;
    }
  }
  Swap(v[div],v[right]);
  return div;
}

归并排序

时间复杂度，O(NlgN)，空间复杂度O(N)，稳定 

void Merge(std::vector<int> &v,int left,int mid,int right,int *newArr)
{
  int begin_1 = left;
  int begin_2 = mid;
  int indexNew = left;

  while(begin_1<mid && begin_2<right)
  {
    if(v[begin_1]<=v[begin_2])
      newArr[indexNew++] = v[begin_1++];
    else 
      newArr[indexNew++] = v[begin_2++];
  }
  while(begin_1<mid)
    newArr[indexNew++] = v[begin_1++];
  while(begin_2<right)
  {
      newArr[indexNew++] = v[begin_2++];
  }
  for(int i = left;i<right;++i)
    v[i] = newArr[i];
}
//左闭右开
void _MergeSort(std::vector<int> &v,int left,int right,int *newArr)
{
  //剩下一个数据退出递归
  if((right-left) == 1)
    return;
  //没有数据退出递归
  if(left>=right)
    return;
  int mid = left + ((right-left)>>1);
  _MergeSort(v,left,mid,newArr);
  _MergeSort(v,mid,right,newArr);
  Merge(v,left,mid,right,newArr);
}
void MergeSort(std::vector<int> &v)
{
  int *newArr = new int[v.size()];
  _MergeSort(v,0,v.size(),newArr);
  delete[] newArr;
}