关于二叉树顺序存储和遍历的概念可以参考 :二叉树的顺序存储
接下来我们讲解一下二叉数的链表存储结构:
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域,我们称这样的链表为二叉链表。
以该树为例
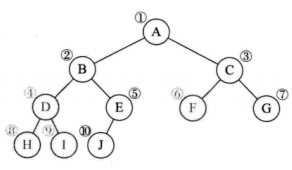
节点结构:
![]()
数结构:
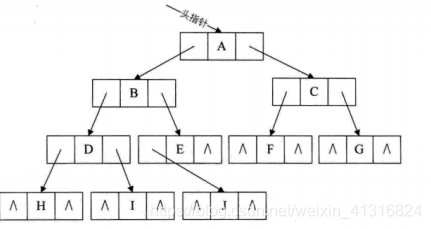
我们当然还可以多开辟一个区域用来存放当前节点的父节点:
![]()
二叉排序树
二叉排序树,又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。
若它的左子树不为空,则左子树上所有的结点的值均小于根结构的值;
若它的右子树不为空,则右字数上所有结点的值均大于它的根结点的值;
它的左右子树也分别为二叉排序树。
1,排序方便
2,方便查找
3,方便插入和删除
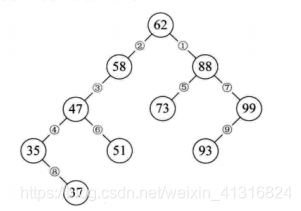
当我们用中序遍历的时候,责输出的是从小到大的值
节点对象:
class BSNode
{
public BSNode LeftChild { get; set; }
public BSNode RightChild { get; set; }
public BSNode Parent { get; set; }
public int data { get; set; }
public BSNode()
{
}
public BSNode(int data)
{
this.data = data;
}
} class BSTree
{
private BSNode root = null;
public void Add(BSNode node)
{
if (root == null)
{
root = node;
return;
}
BSNode tmp = root;
while (true)
{
if (node.data > tmp.data)
{
if (tmp.RightChild == null)
{
tmp.RightChild = node;
node.Parent = tmp;
break;
}
else
{
tmp = tmp.RightChild;
}
}
else
{
if (tmp.LeftChild == null)
{
tmp.LeftChild = node;
node.Parent = tmp;
break;
}
else
{
tmp = tmp.LeftChild;
}
}
}
}
// 前序遍历
public void PreorderTraversal()
{
PreorderTraversal(root);
}
private void PreorderTraversal(BSNode node)
{
if (null == node) return;
Console.Write(node.data + " ");
if (null != node.LeftChild)
{
PreorderTraversal(node.LeftChild);
}
if (null != node.RightChild)
{
PreorderTraversal(node.RightChild);
}
}
// 中序遍历
public void SequentialTraversal()
{
SequentialTraversal(root);
}
private void SequentialTraversal(BSNode node)
{
if (null == root) return;
if (null != node.LeftChild)
{
SequentialTraversal(node.LeftChild);
}
Console.Write(node.data + " ");
if (null != node.RightChild)
{
SequentialTraversal(node.RightChild);
}
}
// 后序遍历
public void PostOrderTraversal()
{
PostOrderTraversal(root);
}
private void PostOrderTraversal(BSNode node)
{
if (null == root) return;
if (null != node.LeftChild)
{
PostOrderTraversal(node.LeftChild);
}
if (null != node.RightChild)
{
PostOrderTraversal(node.RightChild);
}
Console.Write(node.data + " ");
}
public bool Find(int data)
{
return Find(root,data);
}
public bool Find(BSNode node,int data)
{
if (node == null) return false;
if (node.data == data)
{
return true;
}
else
{
if (data < node.data)
{
return Find(node.LeftChild, data);
}
else
{
return Find(node.RightChild, data);
}
}
}
public bool Find2(int data)
{
BSNode tmp = root;
while(true)
{
if (null == tmp) return false;
if (tmp.data == data)
{
return true;
}
else
{
if (data < tmp.data)
{
tmp = tmp.LeftChild;
}
else
{
tmp = tmp.RightChild;
}
}
}
}
public void Delete(int data)
{
BSNode tmp = root;
while (true)
{
if (null == tmp) return;
if (tmp.data == data)
{
Delete(tmp);
break;
}
else
{
if (data < tmp.data)
{
tmp = tmp.LeftChild;
}
else
{
tmp = tmp.RightChild;
}
}
}
}
public void Delete(BSNode node)
{
// 删除的节点 node
// 没有左右子节点时 直接将父节点,指向该节点 置空
if (null == node.LeftChild && null == node.RightChild)
{
if (node.Parent == null)
{
root = null;
}
if (node.Parent.LeftChild == node)
{
node.Parent.LeftChild = null;
}
if (node.Parent.RightChild == node)
{
node.Parent.RightChild = null;
}
}
// 只有左孩子节点时 将node的父节点指向node的左孩子节点
if (null != node.LeftChild && null == node.RightChild)
{
if (node.Parent.LeftChild == node)
{
node.Parent.LeftChild = node.LeftChild;
}
if (node.Parent.RightChild == node)
{
node.Parent.RightChild = node.LeftChild;
}
node.LeftChild.Parent = node.Parent;
node.Parent = null;
}
// 只有右孩子节点时 将node的父节点指向node的右孩子节点
else if (null == node.LeftChild && null != node.RightChild)
{
if (node.Parent.LeftChild == node)
{
node.Parent.LeftChild = node.RightChild;
}
if (node.Parent.RightChild == node)
{
node.Parent.RightChild = node.RightChild;
}
node.RightChild.Parent = node.Parent;
node.Parent = null;
}
// 即有右孩子又有左孩子 两种解决方法
// (一) 找出该节点下的右子树中最小值的节点填到要删除的节点的位置 (根据二叉树排序树的特点 右子树下 遍历左孩子直到没有左孩子时即找到了最小节点)
// (二) 找出该节点下的左子树中最大值的节点填到要删除的节点的位置 (根据二叉树排序树的特点 左子树下 遍历右孩子直到没有左孩子时即找到了最大节点)
else if (null != node.LeftChild && null != node.RightChild)
{
BSNode minRight = node.RightChild;
while (true)
{
if (null == minRight.LeftChild)
{
break;
}
else
{
minRight = minRight.LeftChild;
}
}
node.data = minRight.data;
Delete(minRight);
}
}
} class Program
{
static void Main(string[] args)
{
BSTree tree = new BSTree();
int[] arr = { 62, 58, 88, 47, 73, 99, 35, 51, 93, 37 };
for (int i = 0; i < arr.Length; i++)
{
BSNode node = new BSNode(arr[i]);
tree.Add(node);
// Console.Write(arr[i] + " ");
}
Console.WriteLine();
Console.WriteLine("前序遍历:");
tree.PreorderTraversal();
Console.WriteLine();
Console.WriteLine("中序遍历:");
tree.SequentialTraversal();
Console.WriteLine();
Console.WriteLine("后序遍历:");
tree.PostOrderTraversal();
Console.WriteLine();
tree.Delete(35);
tree.Delete(37);
Console.WriteLine("查找到:" + tree.Find2(88));
tree.SequentialTraversal();
Console.ReadKey();
}
}





















 1171
1171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








