快速排序

快速排序的基本思想：

1、先从序列中取出一个数作为基准数。

2、区分过程，把比这个数大的数全部放到它的右边，小于它的或等于它的数放到左边。

3、再对左右区间重复第二步，直到个个区间只有一个数。

 

快速排序详细步骤：

以一个数组作为示例，取区间第一个数为基准数。

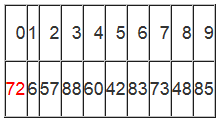
初始时，i = 0;  j = 9;   X = a[i] = 72

由于已经将a[0]中的数保存到X中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。

从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++;  这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j--;

数组变为：

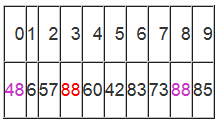
i = 3;   j = 7;   X=72

再重复上面的步骤，先从后向前找，再从前向后找。

从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++

从i开始向后找，当i=5时，由于i==j退出。

此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

数组变为：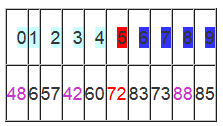

代码实现：

        static void Main(string[] args)
        {
            int[] arr = new int[] { 5, 3, 6, 2, 4, 7 };

            QuickSort(arr,0,arr.Length - 1);
            for (int i = 0; i < arr.Length; i++)
            {
                Console.Write(arr[i] + " ");
            }
            Console.ReadKey();
        }  

        private static void QuickSort(int[] arr,int left,int right)
        {
            if(left < right)
            {
                int x = arr[left];         // 基准数,把比这个数大的数全部放到它的右边，小于它的或等于它的数放到左边。
                int i = left;
                int j = right;

                while(i < j)
                {
                    while(i < j)
                    {
                        if(arr[j] <= x)         // 找到一个小于等于基准数的数把它放再x的左边
                        {
                            arr[i] = arr[j];    // 将比基准数小的数放到空出来的位置
                            break;
                        }
                        else
                        {
                            j--;               // 像左移动继续查找，做比较
                        }
                    }

                    while(i<j)
                    {
                        if (arr[i] > x)         // 找到一个大于基准数的数 把它放再x的又
                        {
                            arr[j] = arr[i];  
                            break;
                        }
                        else
                        {
                            i++;               // 像右查找继续，继续做比较
                        }
                    }
                }

                // 跳出循环 i == j 的时候 责 i 是中间位置
                arr[i] = x;                     // 一轮结束后找到了基准数的位置  然后将数组分成了两个区间   left 到 i - 1 和 i + 1 到 right
                QuickSort(arr,left,i-1);
                QuickSort(arr,i+1,right);
            }
        }

快排总结

1．i =L; j = R; 将基准数挖出形成第一个坑a[i]。

2．j--由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。

3．i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。

4．再重复执行2，3二步，直到i==j，将基准数填入a[i]中。

快速排序优缺点

       快速排序具有最好的平均性能（average behavior），但最坏性能（worst case behavior）和插入排序相同，也是O(n^2)。比如一个序列5,4,3,2,1，要排为1,2,3,4,5。按照快速排序方法，每次只会有一个数据进入正确顺序，不能把数据分成大小相当的两份，很明显，排序的过程就成了一个歪脖子树，树的深度为n，那时间复杂度就成了O(n^2)。尽管如此，需要排序的情况几乎都是乱序的，自然性能就保证了。据书上的测试图来看，在数据量小于20的时候，插入排序具有最好的性能。当大于20时，快速排序具有最好的性能，归并(merge sort)和堆排序(heap sort)也望尘莫及，尽管复杂度都为nlog2(n)。