数据结构 树的非递归遍历10

中序遍历非递归算法思想

中序遍历的几种情况：

分析1：什么时候访问根、什么时候访问左子树、什么访问右子树

             当左子树为空或者左子树已经访问完毕以后，再访问根

             访问完毕根以后，再访问右子树

分析2：为什么是栈，而不是其他（比如说是队列）

             先走到的后访问，后走到的先访问，显然是栈结构

分析3：结点所有路径情况

           步骤1：

                    如果结点有左子树，该结点入栈；

                    如果结点没有左子树，访问该结点；

            步骤2：

                    如果结点有右子树，重复步骤1；

                    如果结点没有右子树（结点访问完毕），根据栈顶指示回值，访问栈顶元素，并访问右子树，重复步骤1

                    如果栈为空，表示遍历结束

注意：入栈的结点表示，本身没有被访问过，同时右子树也没有被访问过

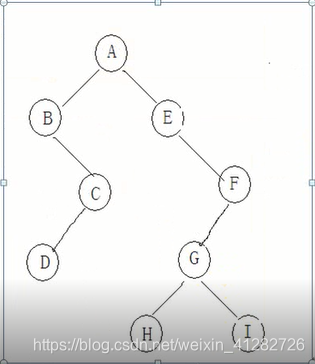
B->D->C->A->E->H->G->I->F

分析4：有一个一直往左走入栈的操作，中序遍历的起点

//中序遍历算法的非递归描述
BiTNode*GoFarLeft(BiTree T,Stack* S)
{
     if(!T)   return NULL;
     while(T->lchild)
     {
       Push(S,T);
       T=T->lchild;
     }
     return T;
}

#include <iostream>
using namespace std;
#include "stack"


//二叉链表示法
struct BiTNode
{
	int data;
	struct BiTNode *lchild, *rchild;
};
typedef struct BiTNode		BiTNode;
typedef struct BiTNode*		BiTree;

/*
步骤1：
如果结点有左子树，该结点入栈；
如果结点没有左子树，访问该结点；
步骤2：
如果结点有右子树，重复步骤1；
如果结点没有右子树（结点访问完毕），根据栈顶指示回退，访问栈顶元素，并访问右子树，重复步骤1
如果栈为空，表示遍历结束。 

*/

//一直向左走,找到中序遍历的起点
BiTNode * goLeft(BiTNode *T, stack<BiTNode *> &s)
{
	if (T == NULL)
	{
		return NULL;
	}
	//判断T有没有左孩子, 没有把Treturn ;
	//如果有 T入栈 ,再往左走
	while(T->lchild != NULL)
	{
		s.push(T);
		T = T->lchild;
	}
	return T;
}
void Inorder2(BiTNode *T)
{
	BiTNode *t = NULL;
	stack<BiTNode *> s;

	t = goLeft(T, s);

	while (t)
	{
		printf("%d ", t->data); //

		//如果t有右子树 重复步骤1
		if (t->rchild != NULL)
		{
			t = goLeft(t->rchild, s); //右子树中中序遍历的起点
		}
		else if (!s.empty()) //如果t没有右子树 根据栈顶指示 回退
		{
			t = s.top();
			s.pop();
		}
		else //如果t没有右子树 并且栈为空  
		{
			t = NULL;
		}
	}

}

void inOrder(BiTNode *root)
{
	if (root == NULL)
	{
		return;
	}
	//遍历左子树
	inOrder(root->lchild);
	printf("%d ", root->data);
	//遍历右子树
	inOrder(root->rchild);
}


void main()
{
	BiTNode t1, t2, t3, t4, t5;
	memset(&t1, 0, sizeof(BiTNode));
	memset(&t2, 0, sizeof(BiTNode));
	memset(&t3, 0, sizeof(BiTNode));
	memset(&t4, 0, sizeof(BiTNode));
	memset(&t5, 0, sizeof(BiTNode));
	t1.data = 1;
	t2.data = 2;
	t3.data = 3;
	t4.data = 4;
	t5.data = 5;

	//建立关系
	t1.lchild = &t2;
	t1.rchild = &t3;
	t2.lchild = &t4;
	t3.lchild = &t5;

	printf("\nolder inorder\n");
	inOrder(&t1);

	printf("\n 非递归遍历\n");
	Inorder2(&t1);
	printf("hello...\n");

	system("pause");
	return ;
}