前面我们已经讲过二叉树的基本操作,现在我们进一步探讨一下B_Tree。B_Tree是一种多叉树,m阶B-Tree满足以下条件:
1、每个节点最多拥有m个子树
2、根节点至少有2个子树
3、分支节点至少拥有m/2颗子树(除根节点和叶子节点外都是分支节点)
4、所有叶子节点都在同一层、每个节点最多可以有m-1个key,并且以升序排列
这四句话看起来是不是有点绕,没事,我们先回顾一下二叉树节点类的定义
public:
int ele;
BtreeNode *left;
BtreeNode *right;
BtreeNode();
BtreeNode(int ele1, BtreeNode *l, BtreeNode *r);
};二叉树节点成员有三个:key值ele,左节点指针left,右节点指针right,而到了多叉树,每个节点的key值不只有一个,所以需要一个数组来存储,另外节点指针也不只是有两个,而是多个,其规则为:节点指针的数目等于主值数组里数据的个数加1,m阶B_Tree代表该B_Tree的单个节点key值有m-1个,对应的子树也就有m个,如图1所示:
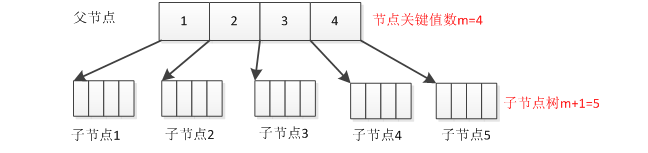
图1
有了这个前提我们来看看B_Tree节点类的定义
class b_Node
{
public:
b_Node *parent;
int key[N+1];//存放关键值
int keynum;
b_Node *ptr[N+1];//分裂时需要用的,假设上一层有一个关键值,对应下一层关键值有两个,如果上一层有两个则下一层有三个,上一层最多3,所以下层最多4个
b_Node();
void show();
};
b_Node::b_Node()
{
parent = 0;
keynum = 0;
for (int i = 0; i < N+1; i++)
ptr[i] = 0;
}key[N+1]是用来存放关键值的,ptr[N+1]是用来存放子节点指针,这里关键值数目与子节点数目个数都是N+1,似乎违反前面说的第四条规则,实际上key[N+1]里虽然能放N+1个值,但后面可以看到有一个位置是用来暂存数据的,数组满了后会将数据分出去,因此key[N+1]里最多还是只能存N个数,不违反第四条规则。另外keynnum是用来记录当前key[N+1]里实际存放数据的数目,parent是指与当前节点有直接连接关系的上一层节点,如图1中五个子节点的parent都是上一层那个父节点:
看完节点类我们来看一下B_Tree树本身,其类定义跟二叉树一样很简单,成员只有根节点root一个
class bTree
{
public:
b_Node *root;
bTree();
result searchKey(b_Node *T,int key);
bool insert(int key_in);
void split(b_Node *sp);
void print_tree();
};
bTree::bTree()
{
root = 0;
}接下来我们看一看如何生成一棵B_Tree,也就是如何对B_Tree进行插入。先附上代码
int search(b_Node *P, int key)
{
int i = 1;
if (key < P->key[i])
return 0;
else if (key>P->key[P->keynum])
return P->keynum;
for (int j = 1; j <= P->keynum; j++)
{
if (key >= P->key[j] && key < P->key[P->keynum])
return j;
}
}
//找某个数在树中的位置,如果找不到,返回应该插入的位置
result bTree::searchKey(b_Node *T,int key)
{
result re;
int i=0;
bool found = false;
b_Node *p=T;
b_Node *q = 0;
while(p != 0&&!found)
{
p->parent = q;
i = search(p, key);
if (i > 0 && p->key[i] == key) found = true;
else
{
q = p;
p = p->ptr[i];//继续往下一层找直到为空
//p->parent = q;
}
}
if (found)
{
re.p = q;
re.i = i;
re.tag = 1;//表示已经找到
}
else
{
re.p = q;
re.i = i+1;
re.tag = 0;
}
return re;
}
bool bTree::insert(int key_in)
{
//先搜索位置
if (root == 0) { root = new b_Node; root->key[1] = key_in; root->keynum++; return true;}
result re = searchKey(root, key_in);
if (re.tag)
{
cout << "the data is existed!" << endl;
return false;
}
else
{
if (re.i <= N)
{
if (re.p->keynum + 1 > N) //考虑顺序需要改变的情况
{
re.p->key[0] = re.p->key[re.p->keynum];
for (int j = re.p->keynum; j > re.i; j--)
re.p->key[j] = re.p->key[j - 1];
re.p->key[re.i] = key_in;
re.p->keynum++;
}
else
{
for (int j = re.p->keynum+1; j > re.i; j--)
re.p->key[j] = re.p->key[j - 1];
re.p->key[re.i] = key_in;
re.p->keynum++;
}
}
else
{
re.p->key[0] = key_in;//暂存
re.p->keynum++;
}
}
if (re.p->keynum <=N) return true;
else
{
split(re.p);
}
}
void bTree::split(b_Node *sp)
{
//首先如果上一层不为空并且还没有满的时候,考虑向上进位
if (sp->parent != 0 && sp->parent->keynum != N)
{
int loc = sp->parent->keynum+1;
sp->parent->key[loc] = sp->key[2];
sp->parent->keynum++;
for (int k = 1; k <= sp->parent->keynum; k++) //找到往上进位的位置
{
if (sp->key[2] > sp->parent->key[k] && sp->key[2]< sp->parent->key[k+1])
{
sp->parent->key[k+1] = sp->key[2];
loc = k+1;
break;
}
}
//将sp->key[2]左右的元素分配好
sp->parent->ptr[loc - 1] = new b_Node;
sp->parent->ptr[loc-1]->key[1]=sp->key[1];
sp->parent->ptr[loc - 1]->keynum++;
sp->parent->ptr[loc] = new b_Node;
for (int l = 3; l <= sp->keynum-1; l++)
{
sp->parent->ptr[loc]->key[l-2]=sp->key[l];
sp->parent->ptr[loc]->keynum++;
}
sp->parent->ptr[loc]->key[sp->keynum-2] = sp->key[0];//0里暂存了最大的元素
sp->parent->ptr[loc]->keynum++;
//sp->keynum--;
}
else //否则自身向下分裂
{
int M = (N + 1) / 2;
for (int i = 1; i < M; i++)
{
sp->ptr[0] = new b_Node;
sp->ptr[0]->key[i] = sp->key[i];
sp->ptr[0]->keynum++;
}
for (int j = M + 1; j <= sp->keynum-1; j++)
{
sp->ptr[1] = new b_Node;
sp->ptr[1]->key[j-2] = sp->key[j];//有问题,下标从0开始
sp->ptr[1]->keynum++;
}
sp->ptr[1]->key[sp->keynum-M] = sp->key[0];
sp->ptr[1]->keynum++;
sp->key[1] = sp->key[M];//剩下元素要清空
sp->keynum = 1;
}
}
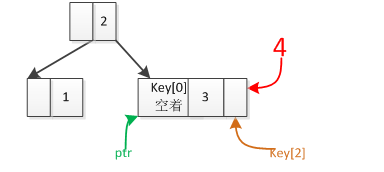
图2
其实B_Tree插入比二叉树的插入要复杂得多,二叉树在插入时只需要找到插入的节点位置在哪,然后将新数据直接插入该位置即可,插入完成后也不需要后续操作。但是B_Tree不一样,需要返回的插入位置信息除了节点位置之外还需要在节点中的具体 位置,如图2所示,将数据4插入树时,除了返回ptr所指向的节点外还应该返回要插入的位置,即3后面的位置。searchKey()就是为了完成这个任务,其中searchKey()里又调用了search()函数,后者负责返回一个位置,前者负责通过返回的位置判断该数据已经在树中存在,还是要进行插入。
插入时,注意一个问题,我们前面说过key[N+1]里只存放N个数据,有一个位置用来暂存数据,这个位置就是key[0](实际上用key[N]似乎更好一些,我一开始定的就是key[0],后面也带来不小麻烦,hh),也就是说我们真正存数据是从key[1]开始的。另外注意如果插入的数据要代替数组中一个数据,那就要该数之后的所有数据往后移动一位,特别注意一种情况,如图3所示,将5插入时,先找到插入的位置在4后面,但是4后面已经有6了,并且6已经没法往后移了,这时候别忘了我们还有key[0]还没有用上,因此将6移到key[0]再插入后,情况就如右边所示。

图3
插入完成不代表就已经万事大吉了,我们已经说过一个节点的key[N+1]里面只能放N个数据,另外还有一个暂存的数据,一共N+1个数,那么如果节点满了怎么办呢,答案就是分裂,也就是split()函数完成的任务。
分裂时有两种情况,我把它形象的成为向上进位和向下分裂。
(1)向上进位,如图4所示,如果当前满的节点上面还有节点,并且上面的节点还没有满,那么可以考虑将当前节点中间的某个数据移到上层节点,再将剩下的数据分为两部分
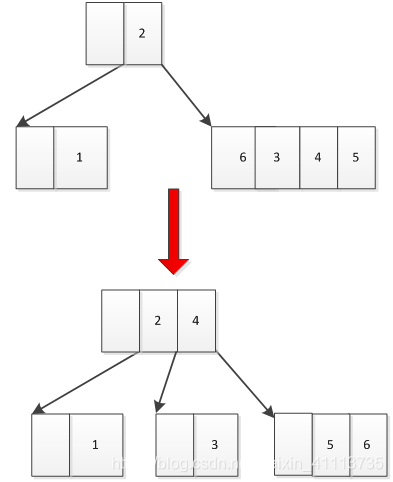
图4
(2)向下分裂,如图5所示,如果当前节点上面已经没有节点了(如根节点root)或者上面节点已经满了,那么就只能考虑向下分裂,将中间某个数据留在层,剩下数据分成两部分,放在下一层。
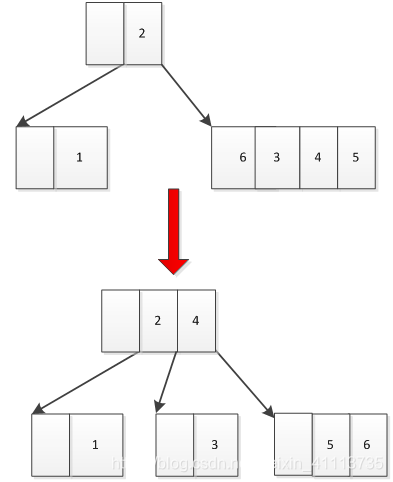
图5
为了更形象的表示我的插入过程,我用一张图表示完整过程,如图6所示,插入数据及顺序为2,4,3,1,5,6,7,8,9,10,11,12,13。
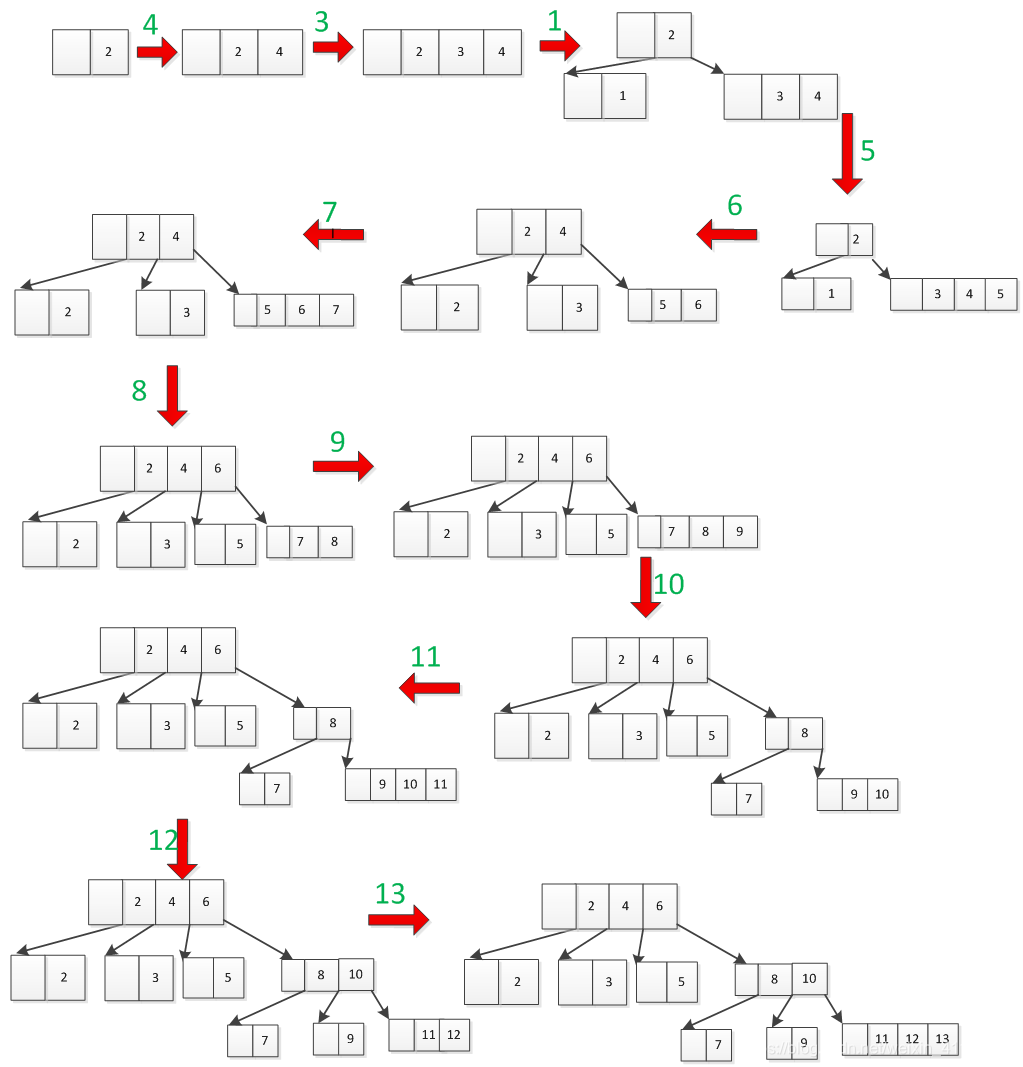
图6
以上就是B_Tree的生成部分,主要是研究怎么对B_Tree进行插入。
工程完整代码可以看我的Github,https://github.com/CrossHand/B_Tree/tree/master
























 915
915

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








