前序、中序和后序遍历
1. 前序遍历
前序遍历(DLR)是二叉树深度优先遍历思想中遍历方法的一种,也称先根遍历等等。前序遍历的思想是根据递归的思想,首先访问的是当前节点的值,即root.val,随后递归进入root.left,待root.left访问完成后,递归进入root.right,若是当前节点为NULL,则return。结合代码更加好理解,下面给出java的前序遍历核心代码,其实就只有三行。
- System.out.println(root.val)
- DLR(root.left)
- DLR(root.right)
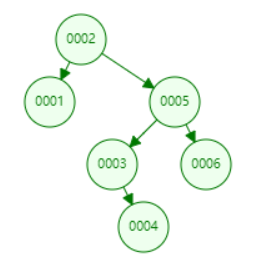
对于上面的二叉树,应用前序遍历的方法,
- (1).首先我们访问当前节点的值为2,随后我们进入左子树
- (2)这时,我们同样要访问当前节点的值,为1,随后我们进入左子树
- (3)因为此时左子树的值为null,所以return ,我们返回到第(2)步,因为第(2)步中,我们已经访问了左子树,随后进入右子树
- (4)因为此时右子树为null,我们退回到第(2)步,此时在第(2)步中,左子树和右子树都已访问完成,所以我们退回到第(1)步,
- (5)在第(1)步中,左子树已经访问完成,我们此时进入右子树
- (6)同样,我们访问当前节点的值为5,随后进入当前节点的左子树
- (7)。。。。
通过上面的步骤,我们可以得到前序遍历的结果为{2,1,5,3,4,6}
public void DLR(TreeNode root){
if(root == null)
return;
System.out.println(root.val); //访问当前节点
DLR(root.left); //进入当前节点的左子树
DLR(root.right); //在完成当前节点左子树的访问之后,进行当前节点右子树的访问
return;
}
2.中序遍历
中序遍历(LDR)同样是二叉树深度优先遍历的一种,中序遍历和前序遍历的思想相同的,中序遍历的思想是:先访问当前节点的左子树,待当前节点左子树完成访问之后,访问当前节点的值,最后进行当前节点右子树的访问
- LDR(root.left)
- System.out.println(root.val);
- LDR (root.right)

同样,对于上面这颗二叉树来说,先进行左子树的访问,在访问当前节点的值,最后进行右子树的访问,可以得到中序遍历的结果为
{1,2,3,4,5,6}.
中序遍历的java实现代码如下:
pubic void LDR(TreeNode root){
if(root == null)
return;
LDR(root.left)
System.out.println(root.val);
LDR(root.right);
return;
}
3.后序遍历
有了前面,前序遍历和中序遍历的解释,后序遍历和前序遍历、中序遍历的不同之处就是在于访问当前节点值的位置,对于前序遍历来说,首先访问当前节点的值,而对于中序遍历来说,中间访问当前节点的值,,显而易见,后序遍历就是,最后访问当前节点的值。
- LRD(root.left)
- LRD(root.right)
- System.out.println(root.val);

那么很容易,对于上面二叉树的后序遍历的结果为,{1,4,3,6,5,2}
同时,代码的实现也就很容易就可以写出
public void LRD(TreeNode root){
if(root == null)
return ;
LRD(root.left);
LRD(root.right);
System.out.println(root.val);
return;
}
总结
这三种遍历方法的核心思想是一样的,区别在于访问当前节点的位置时的顺序,同样我们要理解每种遍历方法的意义,以便于解决不同的问题。







 本文深入解析二叉树的前序、中序和后序遍历方法,详细阐述每种遍历方式的访问顺序及应用场景,附带Java实现代码。
本文深入解析二叉树的前序、中序和后序遍历方法,详细阐述每种遍历方式的访问顺序及应用场景,附带Java实现代码。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








