卷积神经网络的心得体会

1.如何计算卷积后矩阵向量大小？

feature_map尺寸的计算公式为：[（原图片尺寸-卷积核尺寸）/步长]+1，假如原图上尺寸大小是：$3\ast 3$，卷积核大小是$2\ast 2$，步长为1，则卷积后图片大小为，$2\ast 2$；
如下图卷积过程所示：

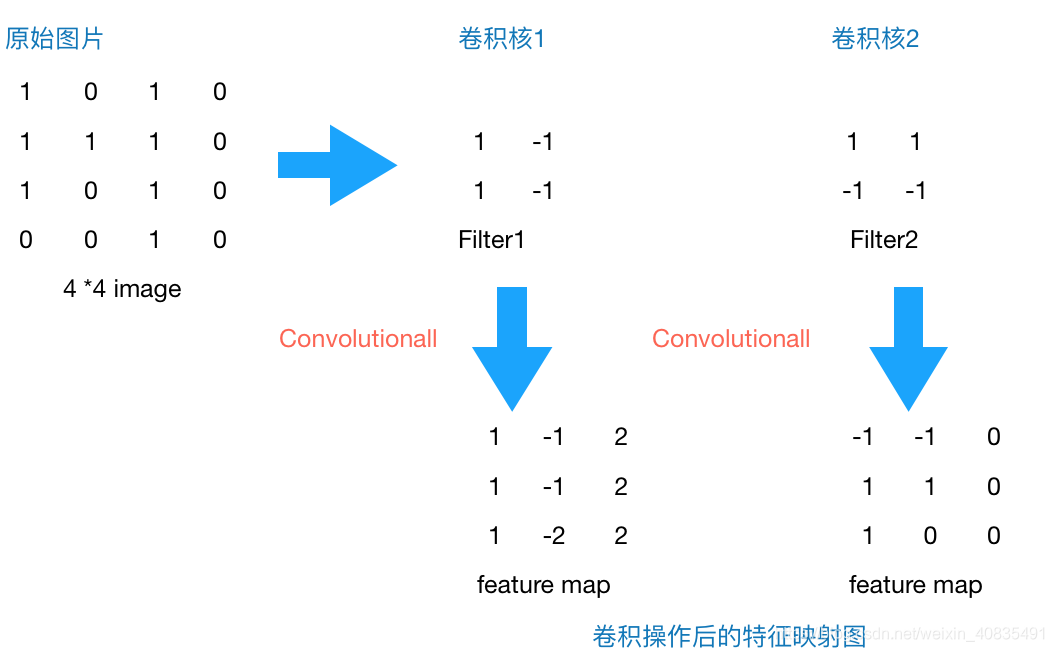
2.为什么卷积核有效？

我们知道，有些卷积核计算后的feature_map是一个3*3的矩阵数据，在第三列的绝对值最大，说明原始图片上对应的地方有一条垂直方向的特征，即像素数值变化较大；而通过第二个卷积核计算后，第三列的数值为0，第二行的数值绝对值最大，说明原始图片上对应的地方有一条水平方向的特征。
　　仔细思考一下，这个时候，我们设计的两个卷积核分别能够提取，或者说检测出原始图片的特定的特征。此时我们其实就可以把卷积核就理解为特征提取器！现在就明白了，为什么我们只需要把图片数据灌进去，设计好卷积核的尺寸、数量和滑动的步长就可以让自动提取出图片的某些特征，从而达到分类的效果啊！

注：

1.此处的卷积运算是两个卷积核大小的矩阵的内积运算，不是矩阵乘法。即相同位置的数字相乘再相加求和。不要弄混淆了。
2.卷积核的公式有很多，这只是最简单的一种。我们所说的卷积核在数字信号处理里也叫滤波器，那滤波器的种类就多了，均值滤波器，高斯滤波器，拉普拉斯滤波器等等，不过，不管是什么滤波器，都只是一种数学运算，无非就是计算更复杂一点。
3.每一层的卷积核大小和个数可以自己定义，不过一般情况下，根据实验得到的经验来看，会在越靠近输入层的卷积层设定少量的卷积核，越往后，卷积层设定的卷积核数目就越多。具体原因大家可以先思考一下，小结里会解释原因。

3.为什么采用Max Pooling？

从计算方式来看，max_pooling算是最简单的一种了，取max即可，但是这也引发一个思考，为什么需要Max Pooling，意义在哪里？如果我们只取最大值，那其他的值被舍弃难道就没有影响吗？不会损失这部分信息吗？如果认为这些信息是可损失的，那么是否意味着我们在进行卷积操作后仍然产生了一些不必要的冗余信息呢？

其实从上文分析卷积核为什么有效的原因来看，每一个卷积核可以看做一个特征提取器，不同的卷积核负责提取不同的特征，我们例子中设计的第一个卷积核能够提取出“垂直”方向的特征，第二个卷积核能够提取出“水平”方向的特征，那么我们对其进行Max Pooling操作后，提取出的是真正能够识别特征的数值，其余被舍弃的数值，对于我提取特定的特征并没有特别大的帮助。那么在进行后续计算使，减小了feature map的尺寸，从而减少参数，达到减小计算量，缺不损失效果的情况。

不过并不是所有情况Max Pooling的效果都很好，有时候有些周边信息也会对某个特定特征的识别产生一定效果，那么这个时候舍弃这部分“不重要”的信息，就不划算了。所以具体情况得具体分析，如果加了Max Pooling后效果反而变差了，不如把卷积后不加Max Pooling的结果与卷积后加了Max Pooling的结果输出对比一下，看看Max Pooling是否对卷积核提取特征起了反效果。

4. 卷积核的尺寸必须为正方形吗？可以为长方形吗？如果是长方形应该怎么计算？

卷积核的尺寸不一定非得为正方形，长方形也可以，只不过通常情况下为正方形。如果要设置为长方形，那么首先得保证这层的输出形状是整数，不能是小数。如果你的图像是边长为 28 的正方形。那么卷积层的输出就满足 [ (28 - kernel_size)/ stride ] + 1 ，这个数值得是整数才行，否则没有物理意义。譬如，你算得一个边长为 3.6 的 feature map 是没有物理意义的。 pooling 层同理。FC 层的输出形状总是满足整数，其唯一的要求就是整个训练过程中 FC 层的输入得是定长的。如果你的图像不是正方形。那么在制作数据时，可以缩放到统一大小（非正方形），再使用非正方形的 kernel_size 来使得卷积层的输出依然是整数。总之，撇开网络结果设定的好坏不谈，其本质上就是在做算术应用题：如何使得各层的输出是整数。

5…卷积核的个数如何确定？每一层的卷积核的个数都是相同的吗？

由经验确定。通常情况下，靠近输入的卷积层，譬如第一层卷积层，会找出一些共性的特征，如手写数字识别中第一层我们设定卷积核个数为5个，一般是找出诸如"横线"、“竖线”、“斜线”等共性特征，我们称之为basic feature（基本特征，简单特征），经过max pooling后，在第二层卷积层，设定卷积核个数为20个，可以找出一些相对复杂的特征，如“横折”、“左半圆”、“右半圆”等特征，越往后，卷积核设定的数目越多，越能体现label的特征就越细致，就越容易分类出来，打个比方，如果你想分类出“0”的数字，你看到这个特征，能推测是什么数字呢？只有越往后，检测识别的特征越多，试过能识别这几个特征，那么我就能够确定这个数字是“0”。

6.步长的向右和向下移动的幅度必须是一样的吗？

有stride_w和stride_h，后者表示的就是上下步长。如果用stride，则表示stride_h=stride_w=stride，也就是说上下左右移动的步长可以不一样。

7.对于含有RGB三种颜色的图片来讲，我们应该如何确定卷积核函数大小以及深度，和核函数的个数？

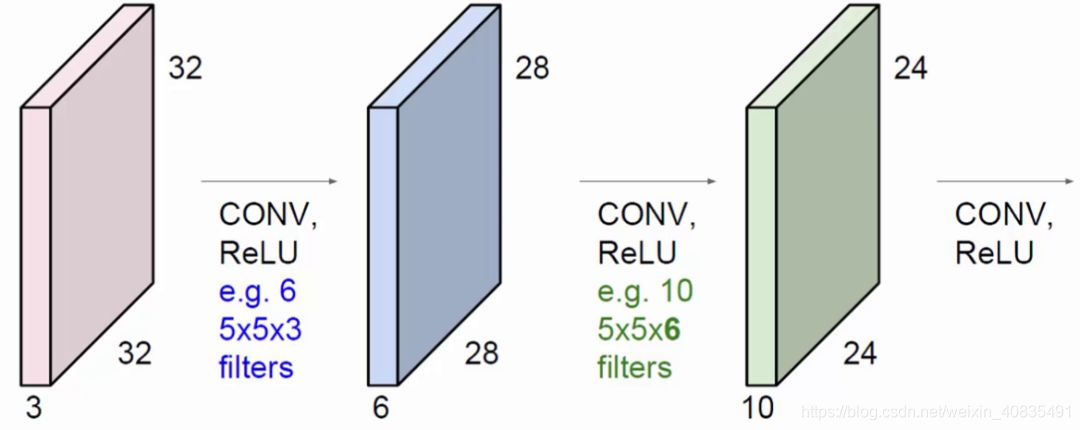
假设输入图片大小为$32\ast 32\ast 3$，其中的3代表深度，表示为RGB三个颜色；第一个卷积层的大小为$5\ast 5\ast 3$，这里我们也可以把卷积层的大小表示为：$5\ast 5$，因为原输入图片中的深度大小必须和卷积神经网路中的卷积深度大小一致才可以，这个深度不同于卷积核的个数，卷积核的个数为输出的特征图个数。将不同深度的卷积核和原图片进行卷积操作，然后将输出肚饿三个不同的值进行相加，形成一个值。按照这个思路的话，我们将$32\ast 32\ast 3$的图片和6个相同的大小为$5\ast 5\ast 3$的卷积核进行卷积后，形成$28\ast 28\ast 6$的图片大小。这里的6表示6个卷积核，一个卷积核的话只会形成$28\ast 28\ast 1$的图片。
总结：卷积核的个数可以随机定义，但是卷积核的个数越多，刻画的特征也就越细致。而卷积核的深度必须和待卷积的深度相同才可以。

参考文献：https://www.cnblogs.com/charlotte77/p/7759802.html