递归

用栈的数据结构，加上一个简单的逻辑算法实现了业务功能。
递归需要满足的三个条件

1. 一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
3. 存在递归终止条件
   写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，
   最后将递推公式和终止条件翻译成代码。

例子：
假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？
分析：
第一类是第一步走了 1 个台阶，
另一类是第一步走了 2 个台阶。
所以 n 个台阶的走法就等于先走 1 阶后，n-1 个台阶的走法
加上先走 2 阶后，n-2 个台阶的走法。

f(n) = f(n-1)+f(n-2)

递归终止条件就是 f(1)=1，f(2)=2。

int f(int n) { 
	if (n == 1) return 1;
	if(n == 2) return 2;
	return f(n-1)+f(n-2);

理解：如果一个问题A可以分解为若干子问题B,C,D,你可以假设子问题B,C,D已经解决，在此基础上思考如何解决问题A。而且，你只需要思考问题A与子问题B,C,D两层之间的关系即可，不需要一层层往下撕开子问题与子子问题。

避免重复计算问题：

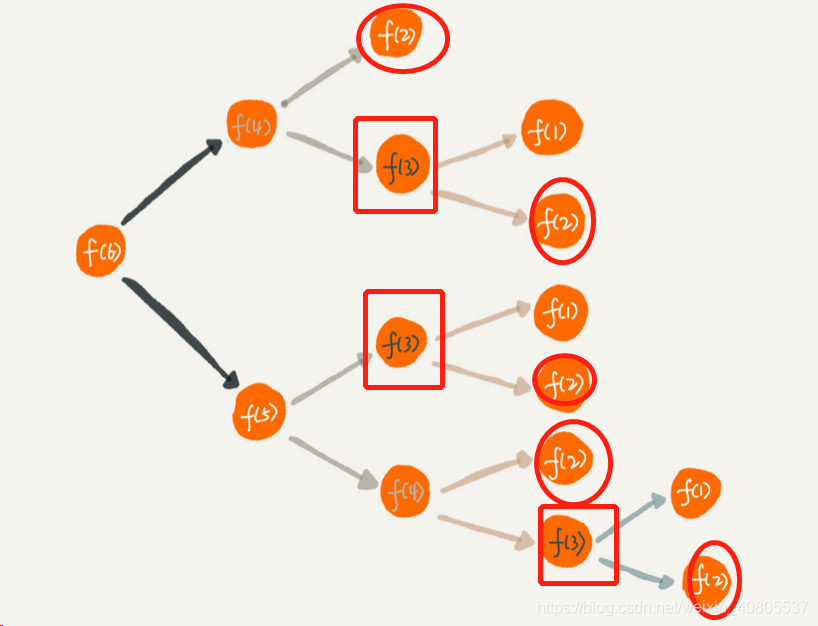
我们可以通过一个散列表来保存已经求解过的值。
如：

//可以先定义一个成员变量
Map<Integer,Integer> map  = new HashMap<Integer,Integer>();
public int f(int n){
	if(n==1) return 1;
	if(n==2) return 2;

	if(map.containsKey(n)){
		return map.get(n);
	}
	int ret = f(n-1)+f(n-2);
	map.put(n,ret);
	return ret;
}

递归代码的表达力很强，写起来非常简洁；
而弊就是空间复杂度高、有堆栈溢出的风险、存在重复计算、过多的函数调用会耗时较多等问题。

五、递归常见问题及解决方案
1.警惕堆栈溢出：可以声明一个全局变量来控制递归的深度，从而避免堆栈溢出。
2.警惕重复计算：通过某种数据结构来保存已经求解过的值，从而避免重复计算。