红黑树

平衡二叉查找树
平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于 1。
红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中，复杂度退化的问题而产生的。红黑树的高度近似 log2n，所以它是近似平衡，插入、删除、查找操作的时间复杂度都是 O(logn)。

红黑树特点:
每个节点非红即黑；
根节点总是黑色的；
每个叶子节点都是黑色的空节点（NIL节点），不存储数据；
如果节点是红色的，则它的子节点必须是黑色的（红色节点不能相邻，反之不一定）；
从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）

红黑树中去掉红色节点，会退化成完全二叉树。高度为log2n
因为相邻的节点不能同时出现红色，所以红色节点会间隔出现在红黑树中，加入节点后，最长的路径也不会超过2log2n。

TreeMap、TreeSet以及JDK1.8之后的HashMap底层都用到了红黑树。

Treap、Splay Tree，绝大部分情况下，它们操作的效率都很高，但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大，但是对于单次操作时间非常敏感的场景来说，它们并不适用。
AVL 树是一种高度平衡的二叉树，所以查找的效率非常高，但是，AVL 树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用 AVL 树代价就有点高了。
红黑树只是做到了近似平衡，并不是严格的平衡，所以在维护平衡的成本上，要比 AVL 树要低。所以，红黑树的插入、删除、查找各种操作性能都比较稳定。

插入：
红黑树规定，插入的节点必须是红色的。而且，二叉查找树中新插入的节点都是放在叶子节点上。
如果插入节点的父节点是黑色的，那我们什么都不用做，它仍然满足红黑树的定义。
如果插入的节点是根节点，那我们直接改变它的颜色，把它变成黑色就可以了。
其他情况都会违背红黑树的定义：调整包括：左右旋转和改变颜色。
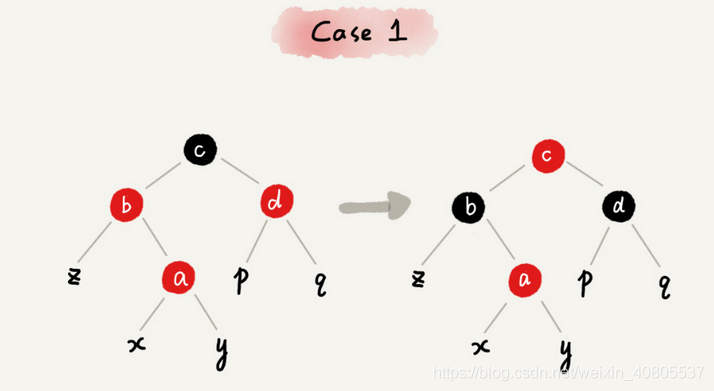
CASE 1：如果关注节点是 a，它的叔叔节点 d 是红色。
1 将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色；
2 将关注节点 a 的祖父节点 c 的颜色设置成红色；
3 关注节点变成 a 的祖父节点 c；
4 跳到 CASE 2或者 CASE 3。

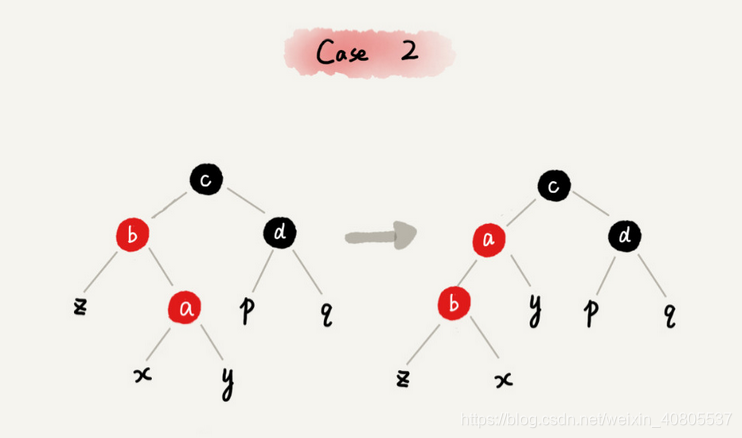
CASE 2：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的右子节点
1 关注节点变成节点 a 的父节点 b；
2 围绕新的关注节点b 左旋；
3 跳到 CASE 3。

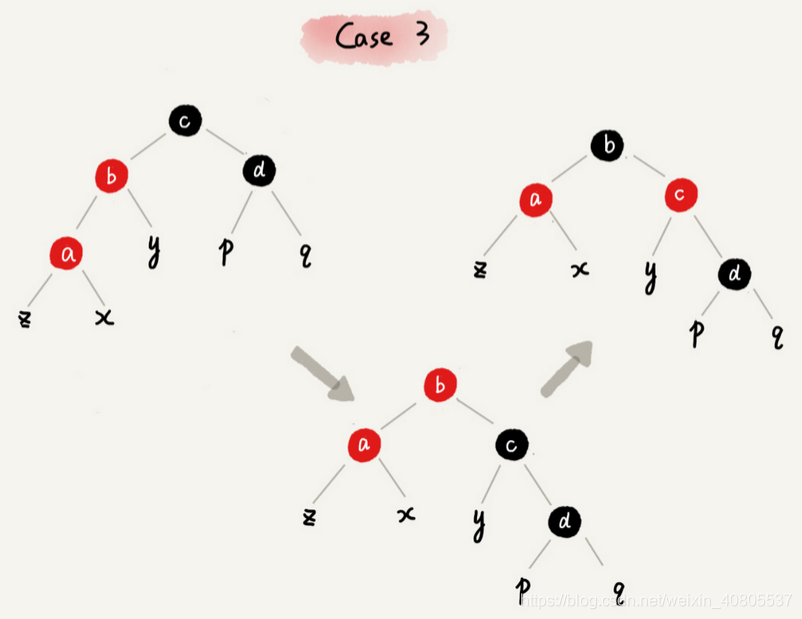
CASE 3：如果关注节点是 a，它的叔叔节点 d 是黑色，关注节点 a 是其父节点 b 的左子节点
1 围绕关注节点 a 的祖父节点 c 右旋；
2 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换。
3 调整结束。

删除
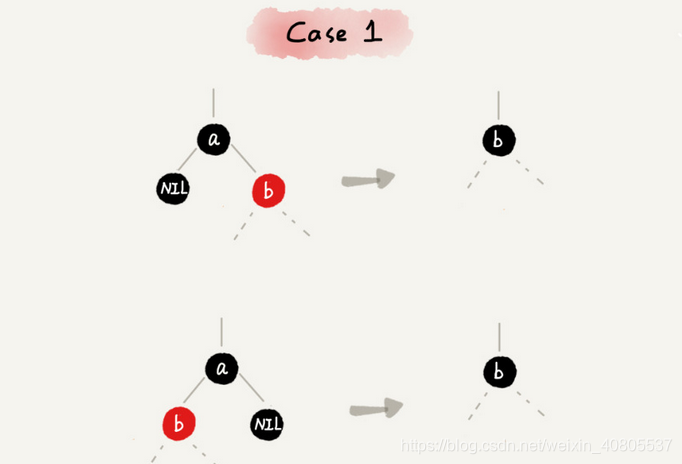
CASE 1：如果要删除的节点是 a，它只有一个子节点 b
1 删除节点 a，并且把节点 b 替换到节点 a 的位置，这一部分操作跟普通的二叉查找树的删除操作一样；
2 节点 a 只能是黑色，节点 b 也只能是红色，其他情况均不符合红黑树的定义。这种情况下，我们把节点 b 改为黑色；
3 调整结束，不需要进行二次调整。

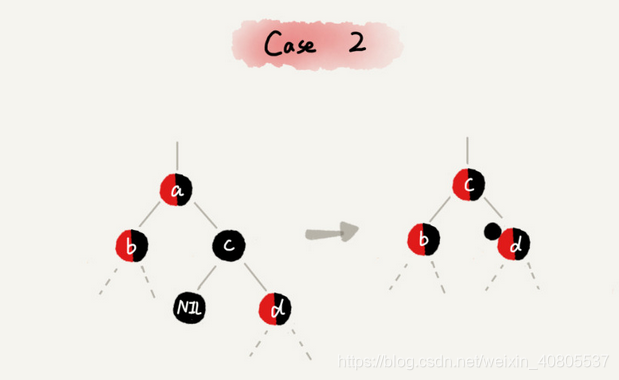
CASE 2：如果要删除的节点 a 有两个非空子节点，并且它的后继节点就是节点 a 的右子节点 c。
1 如果节点 a 的后继节点就是右子节点 c，那右子节点 c 肯定没有左子树。我们把节点 a 删除，并且将节点 c 替换到节点 a 的位置。这一部分操作跟普通的二叉查找树的删除操作无异；
2 然后把节点 c 的颜色设置为跟节点 a 相同的颜色；
3 如果节点 c 是黑色，为了不违反红黑树的最后一条定义，我们给节点 c 的右子节点 d 多加一个黑色，这个时候节点 d 就成了“红 - 黑”或者“黑 - 黑”；
4 这个时候，关注节点变成了节点 d，第二步的调整操作就会针对关注节点来做。

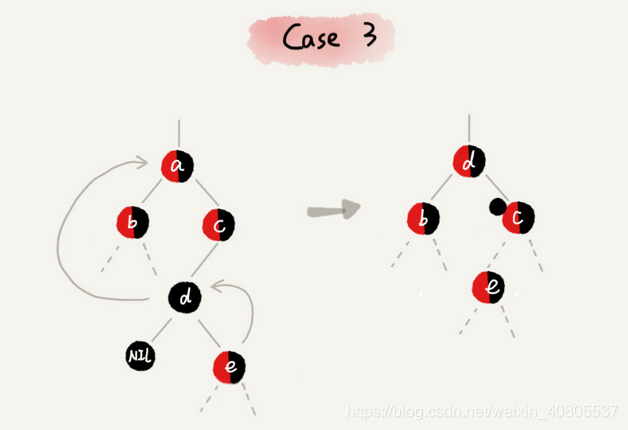
CASE 3：如果要删除的是节点 a，它有两个非空子节点，并且节点 a 的后继节点不是右子节点
1 找到后继节点 d，并将它删除，删除后继节点 d 的过程参照CASE 1；
2 将节点 a 替换成后继节点 d；
3 把节点 d 的颜色设置为跟节点 a 相同的颜色；
4 如果节点 d 是黑色，为了不违反红黑树的最后一条定义，我们给节点 d 的右子节点 c 多加一个黑色，这个时候节点 c 就成了“红 - 黑”或者“黑 - 黑”；
5 这个时候，关注节点变成了节点 c，第二步的调整操作就会针对关注节点来做。

针对关注节点进行二次调整
CASE 1：如果关注节点是 a，它的兄弟节点 c 是红色的
1 围绕关注节点 a 的父节点 b 左旋；
2 关注节点 a 的父节点 b 和祖父节点 c 交换颜色；
3 关注节点不变；
4 继续从四种情况中选择适合的规则来调整。

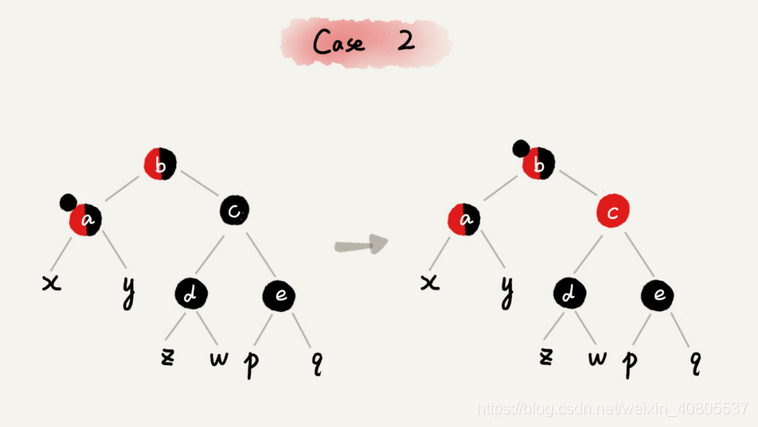
CASE 2：如果关注节点是 a，它的兄弟节点 c 是黑色的，并且节点 c 的左右子节点 d、e 都是黑色的
1 将关注节点 a 的兄弟节点 c 的颜色变成红色；
2 从关注节点 a 中去掉一个黑色，这个时候节点 a 就是单纯的红色或者黑色；
3 给关注节点 a 的父节点 b 添加一个黑色，这个时候节点 b就变成了“红 - 黑”或者“黑 - 黑”；
4 关注节点从 a 变成其父节点 b；
5 继续从四种情况中选择符合的规则来调整

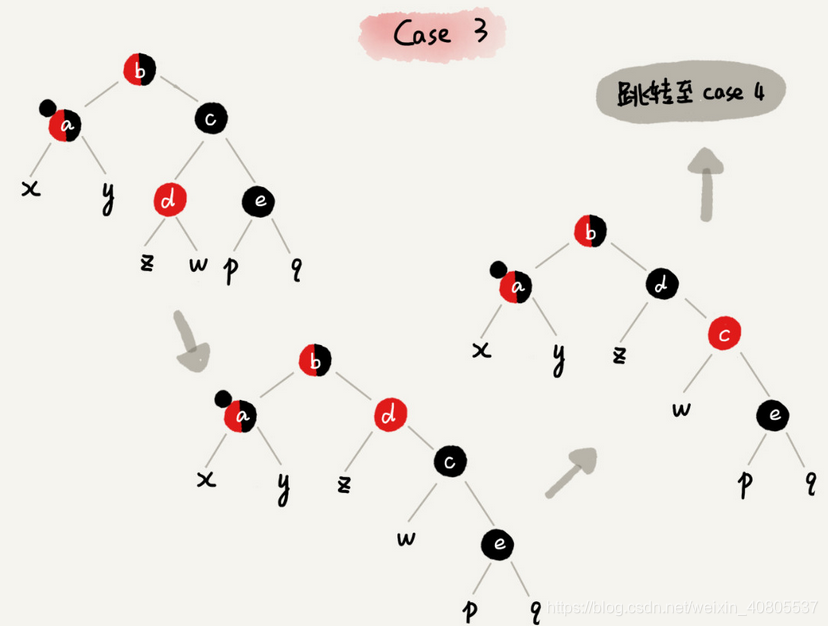
CASE 3：如果关注节点是 a，它的兄弟节点 c 是黑色，c 的左子节点 d 是红色，c 的右子节点 e 是黑色
1 围绕关注节点 a 的兄弟节点 c 右旋；
2 节点 c 和节点 d 交换颜色；
3 关注节点不变；
4 跳转到 CASE 4，继续调整。

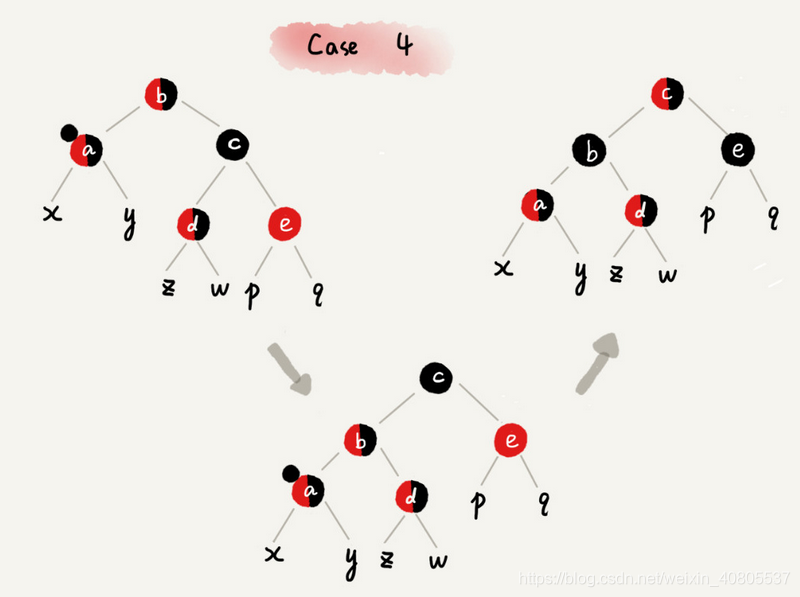
CASE 4：如果关注节点 a 的兄弟节点 c 是黑色的，并且 c 的右子节点是红色的
1 围绕关注节点 a 的父节点 b 左旋；
2 将关注节点 a 的兄弟节点 c 的颜色，跟关注节点 a 的父节点 b 设置成相同的颜色；
3 将关注节点 a 的父节点 b 的颜色设置为黑色；
4 从关注节点 a 中去掉一个黑色，节点 a 就变成了单纯的红色或者黑色
5 将关注节点 a 的叔叔节点 e 设置为黑色；
6 调整结束。

转载自王争老师的《数据结构与算法之美》