边界提取

孔洞填充

X0是一副全黑的图像,但在孔洞的地方有一个白点。

我们要对A图进行孔洞填充,首先求出A的补集作为备用,然后所用到的element B如上图。首先我们构建X0一幅全黑图像加上孔洞中的一点白作为初始图像,然后用B对X0进行膨胀,结果膨胀的结果超过了孔洞的大小,于是用之前构造的Ac对其求交集将其结果限制在孔洞内(由于我们的element是一个四连通元素,每一次膨胀其边界不会超出一个像素点,而由于Ac 的四周都是一个像素宽的沟壑,所以求交集刚好能限制膨胀过界的像素)。然后迭代,直到xk−1 与xk相同。最后得到孔洞的填充图像,最后与原图像求并集刚好就把孔洞填充了。
如果选择Element为八连通,将无法成功限制膨胀的溢出和越界。
连通分量提取

与空洞填充类似,迭代至Xk-1 与 Xk相同为止。连通分量提取常用语自动检测,检测外来物。
凸壳
凸壳是为了找到一个凹陷的物体最小外壳,以不完美命中(腐蚀)为主要操作,通过调整结构元,加上原图,得到相关结果。公式如下:

该方法反复对A进行击中或击不中变换操作,当不再发生变化时,执行并集操作。

为了确保在上述生长过程中凸壳不会大幅度超过凸性所需的最小尺寸,可以限制其生长以便凸壳不会超出初始时包含物体A的最小矩形。
细化
图像细化的目的是提取骨架,根据击中和击不中变换来定义

以结构元的序列为基础定义细化:
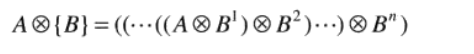
其中B的定义为:
![]()
Bi 是 Bi-1旋转后的结果。A被B1细化一次,得到的结果被B2细化一次.....循环,直到不再发生变化。每次单独细化,使用第一个公式。
粗化
粗化是形态学的对偶,定义如下

B是适合于粗化处理的结构元,与细化一样。粗化处理也可以定义为一个系列操作:
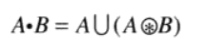

























 1521
1521

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










