DeepWalk无监督学习网络中节点的潜在表示
输入:网络
输出:节点的低维向量表示
亮点:(1)random walk提取中心顶点的邻居序列,可并行(设置多个walkers)。(2)使用language model Skip-Gram算法
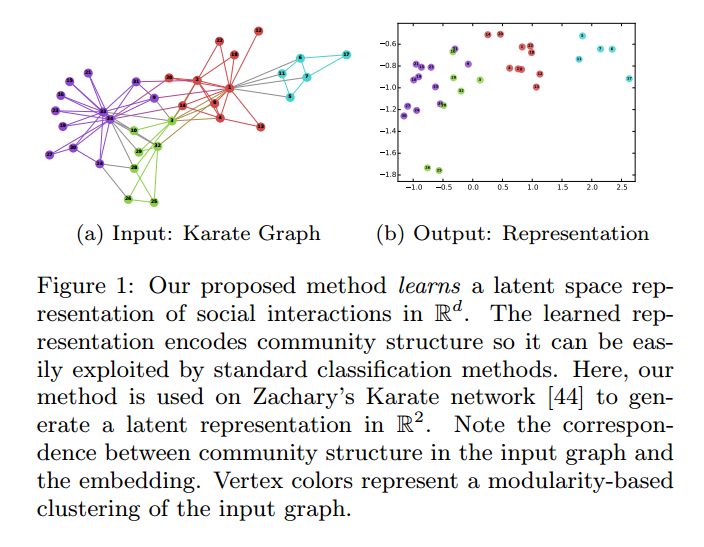
a是输入的Karate Graph, b是输出二维潜在向量表示,节点颜色代表聚类的簇,左右两种表达具有惊人的相似性,而且b中线性可分。
学习到的表示具有以下特点
- 适应性
- 社区意识,潜在特征向量之间的距离应该能够反应网络中社交成员之间的社交相似性。
- 低维度
- 连续
贡献:
- DeepWalk学习当前结构规律
- Micro F1算法评估
- 阐述并行和流式拓展
传统关系分类方法,将问题作为无向马尔科夫网络的推断,使用迭代近似推理算法
random walk选择顶点 v i v_i vi的邻居顶点的集合
顶点度的分布服从幂率,顶点出现在random walk的频率也服从幂律分布。之所以要进行这样的比较是为了根据节点出现的频率创建节点的huffman树。
幂律分布

DeepWalk

输入:
输出:

并行
ASGD异步随机梯度下降

算法变化
Streamimg
Non-random walks
调参
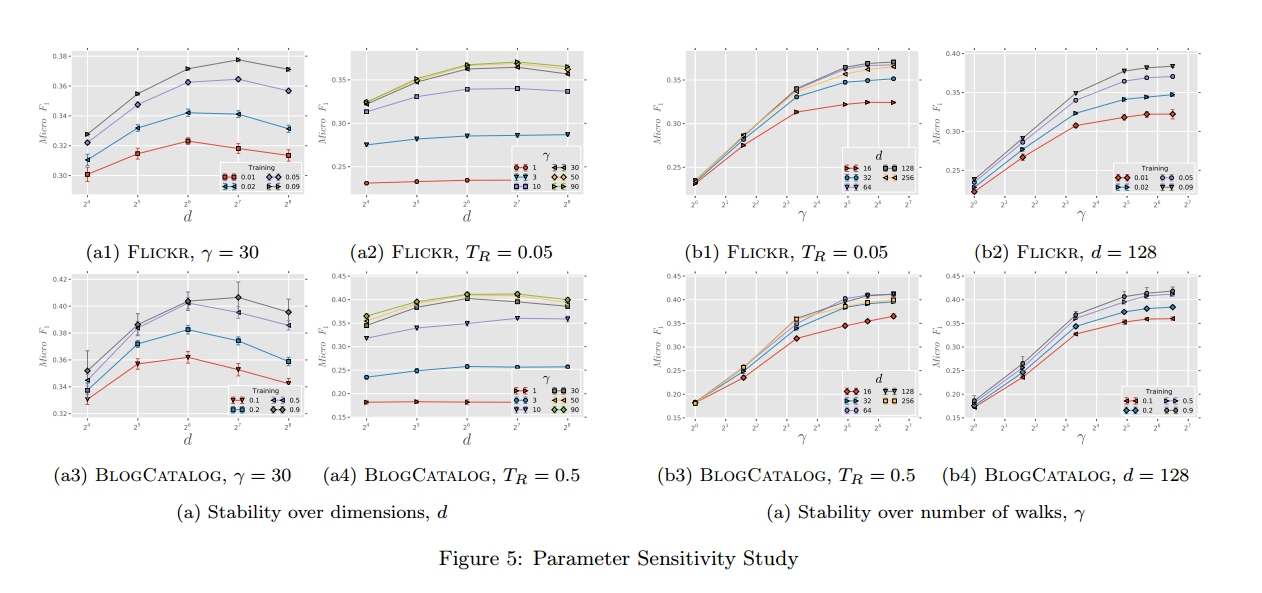








 本文介绍了一种名为DeepWalk的无监督学习方法,该方法通过randomwalk抽取网络中节点的邻居序列,并利用Skip-Gram算法生成节点的低维向量表示。这些表示不仅能够反映节点间的社交相似性,还具有适应性和连续性的特点。文章还探讨了DeepWalk的并行实现及流式拓展。
本文介绍了一种名为DeepWalk的无监督学习方法,该方法通过randomwalk抽取网络中节点的邻居序列,并利用Skip-Gram算法生成节点的低维向量表示。这些表示不仅能够反映节点间的社交相似性,还具有适应性和连续性的特点。文章还探讨了DeepWalk的并行实现及流式拓展。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








